How Can I Learn Trigonometry Easily? A Comprehensive Guide

Trigonometry, the branch of mathematics dealing with relationships between angles and sides of triangles, can seem daunting. But, How Can I Learn Trigonometry Easily? This comprehensive guide, presented by LEARNS.EDU.VN, simplifies trigonometry through visualizations, real-world applications, and proven learning strategies. Unlock the secrets of trigonometric functions, master problem-solving techniques, and discover resources that make learning trigonometry an engaging and rewarding experience. Let’s explore trigonometric concepts with clarity, focusing on practical understanding and effective study methods.

1. Understanding the Fundamentals of Trigonometry

Trigonometry is built upon a few core concepts. Grasping these fundamentals is crucial for easy learning.

1.1. Basic Trigonometric Ratios

The three primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios relate the angles of a right triangle to the lengths of its sides.

• Sine (sin): Defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse.
• Cosine (cos): Defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
• Tangent (tan): Defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.

The mnemonic SOH-CAH-TOA is often used to remember these ratios:

• SOH: Sine = Opposite / Hypotenuse
• CAH: Cosine = Adjacent / Hypotenuse
• TOA: Tangent = Opposite / Adjacent

1.2. The Unit Circle

The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. It provides a visual representation of trigonometric functions.

• Angles: Measured in radians or degrees, starting from the positive x-axis.
• Coordinates: The x-coordinate of a point on the unit circle corresponds to the cosine of the angle, and the y-coordinate corresponds to the sine of the angle.
• Tangent: Represented as the slope of the line from the origin to the point on the circle.

The unit circle helps in understanding the periodic nature of trigonometric functions and their values at different angles.

1.3. Pythagorean Theorem and Trigonometry

The Pythagorean theorem ($a^2 + b^2 = c^2$) is fundamental in trigonometry. It relates the sides of a right triangle, where a and b are the lengths of the two shorter sides (legs), and c is the length of the longest side (hypotenuse).

In the context of the unit circle:

• If a is the cosine and b is the sine of an angle, then $cos^2(θ) + sin^2(θ) = 1$.
• This identity is a cornerstone of trigonometric proofs and simplifications.

2. Visualizing Trigonometric Functions

Visual aids can significantly simplify learning trigonometry. Visualizing trigonometric functions helps in understanding their behavior and properties.

2.1. Graphs of Sine, Cosine, and Tangent

Graphs of trigonometric functions illustrate their periodic nature and key characteristics.

• Sine (sin x): A wave that oscillates between -1 and 1, with a period of $2π$.
• Cosine (cos x): Similar to sine, but shifted by $π/2$, also oscillating between -1 and 1 with a period of $2π$.
• Tangent (tan x): Has vertical asymptotes and a period of $π$, ranging from negative infinity to positive infinity.

Understanding these graphs helps in recognizing patterns and predicting function values.

2.2. Amplitude, Period, and Phase Shift

These parameters define the characteristics of trigonometric functions.

• Amplitude: The maximum displacement from the x-axis. For $y = A sin(x)$ or $y = A cos(x)$, the amplitude is |A|.
• Period: The length of one complete cycle of the function. For $y = sin(Bx)$ or $y = cos(Bx)$, the period is $2π/|B|$.
• Phase Shift: A horizontal shift of the function. For $y = sin(x – C)$ or $y = cos(x – C)$, the phase shift is C.

Adjusting these parameters changes the shape and position of the trigonometric graphs, providing a deeper understanding of their behavior.

2.3. Real-World Visualizations

Trigonometry is not just an abstract concept; it has many real-world applications that can aid understanding.

• Waves: Sound waves, light waves, and water waves can be modeled using trigonometric functions.
• Oscillations: Pendulums, springs, and other oscillating systems exhibit trigonometric behavior.
• Navigation: Used in GPS systems, aviation, and maritime navigation to calculate distances and directions.
• Architecture: Used to design and analyze structures, ensuring stability and aesthetic appeal.

By recognizing trigonometry in everyday phenomena, learners can better appreciate its relevance and usefulness.

3. Effective Learning Strategies for Trigonometry

Adopting the right learning strategies can make mastering trigonometry much easier.

3.1. Breaking Down Complex Problems

Complex trigonometric problems can be simplified by breaking them down into smaller, manageable steps.

1. Identify the Given Information: Determine what angles and side lengths are provided in the problem.
2. Choose the Appropriate Trigonometric Ratio: Select the correct ratio (sin, cos, tan) based on the given information and what needs to be found.
3. Set Up the Equation: Write the equation using the chosen trigonometric ratio.
4. Solve for the Unknown: Use algebraic techniques to solve for the unknown angle or side length.
5. Check the Solution: Verify the solution by plugging it back into the original equation or using other trigonometric identities.

3.2. Using Mnemonics and Memory Aids

Mnemonics are helpful for memorizing trigonometric identities and formulas.

• SOH-CAH-TOA: Already mentioned, a fundamental mnemonic for basic trigonometric ratios.
• CAST Rule: Indicates which trigonometric functions are positive in each quadrant of the unit circle (Quadrant I: All, Quadrant II: Sine, Quadrant III: Tangent, Quadrant IV: Cosine).
• “Some Old Horses Catch Apples Happily Today Over America”: A creative mnemonic for sine, cosine, tangent, cotangent, secant, cosecant in terms of opposite, adjacent, and hypotenuse.

3.3. Practice Regularly

Consistent practice is essential for mastering trigonometry.

• Solve a Variety of Problems: Work through different types of trigonometric problems to develop a strong understanding of the concepts.
• Use Practice Worksheets and Quizzes: Utilize available resources for regular practice and self-assessment.
• Review Mistakes: Analyze mistakes to identify areas that need improvement and reinforce correct methods.

3.4. Applying Trigonometry to Real-World Scenarios

Real-world applications can make trigonometry more relatable and easier to understand.

• Surveying: Use trigonometry to measure distances and angles in surveying.
• Engineering: Apply trigonometric principles in structural engineering and design.
• Physics: Understand projectile motion and wave phenomena using trigonometry.
• Astronomy: Calculate distances and angles in astronomical observations.

4. Essential Trigonometric Identities and Formulas

Trigonometric identities and formulas are essential tools for simplifying expressions and solving equations.

4.1. Fundamental Trigonometric Identities

These are the basic identities that form the foundation of trigonometry.

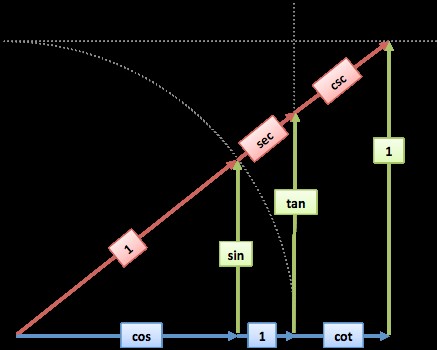
• Reciprocal Identities:
  • $csc(x) = frac{1}{sin(x)}$
  • $sec(x) = frac{1}{cos(x)}$
  • $cot(x) = frac{1}{tan(x)}$
• Quotient Identities:
  • $tan(x) = frac{sin(x)}{cos(x)}$
  • $cot(x) = frac{cos(x)}{sin(x)}$
• Pythagorean Identities:
  • $sin^2(x) + cos^2(x) = 1$
  • $1 + tan^2(x) = sec^2(x)$
  • $1 + cot^2(x) = csc^2(x)$

4.2. Angle Sum and Difference Formulas

These formulas are used to find trigonometric functions of sums and differences of angles.

• $sin(A + B) = sin(A)cos(B) + cos(A)sin(B)$
• $sin(A – B) = sin(A)cos(B) – cos(A)sin(B)$
• $cos(A + B) = cos(A)cos(B) – sin(A)sin(B)$
• $cos(A – B) = cos(A)cos(B) + sin(A)sin(B)$
• $tan(A + B) = frac{tan(A) + tan(B)}{1 – tan(A)tan(B)}$
• $tan(A – B) = frac{tan(A) – tan(B)}{1 + tan(A)tan(B)}$

4.3. Double Angle Formulas

These formulas are used to find trigonometric functions of double angles.

• $sin(2x) = 2sin(x)cos(x)$
• $cos(2x) = cos^2(x) – sin^2(x) = 2cos^2(x) – 1 = 1 – 2sin^2(x)$
• $tan(2x) = frac{2tan(x)}{1 – tan^2(x)}$

4.4. Half Angle Formulas

These formulas are used to find trigonometric functions of half angles.

• $sin(frac{x}{2}) = pm sqrt{frac{1 – cos(x)}{2}}$
• $cos(frac{x}{2}) = pm sqrt{frac{1 + cos(x)}{2}}$
• $tan(frac{x}{2}) = frac{sin(x)}{1 + cos(x)} = frac{1 – cos(x)}{sin(x)}$

5. Trigonometry in Different Contexts

Understanding how trigonometry is applied in various fields can provide a broader perspective and deeper appreciation.

5.1. Solving Triangles

Solving triangles involves finding the unknown angles and side lengths using trigonometric ratios and laws.

• Right Triangles: Use SOH-CAH-TOA to find missing sides and angles.
• Oblique Triangles: Use the Law of Sines and the Law of Cosines.
  • Law of Sines: $frac{a}{sin(A)} = frac{b}{sin(B)} = frac{c}{sin(C)}$
  • Law of Cosines: $c^2 = a^2 + b^2 – 2abcos(C)$

5.2. Navigation and Surveying

Trigonometry is essential for navigation and surveying.

• Triangulation: Use trigonometry to determine the location of a point by forming triangles to known points.
• Bearing: Use angles to specify direction in navigation.
• GPS Systems: Use trigonometry to calculate positions based on signals from satellites.

5.3. Physics and Engineering

Trigonometry is used extensively in physics and engineering.

• Vectors: Represent forces, velocities, and accelerations as vectors and use trigonometry to analyze their components.
• Wave Motion: Model wave phenomena using trigonometric functions.
• Structural Analysis: Analyze the forces and stresses in structures using trigonometry.

6. Common Mistakes and How to Avoid Them

Avoiding common mistakes can save time and improve accuracy in trigonometry.

6.1. Incorrectly Applying Trigonometric Ratios

Ensure you are using the correct trigonometric ratio (sin, cos, tan) based on the given information.

• Mistake: Confusing opposite and adjacent sides.
• Solution: Always label the sides of the triangle relative to the angle in question.

6.2. Forgetting the Unit Circle

The unit circle is a valuable tool for remembering trigonometric values.

• Mistake: Not knowing the values of trigonometric functions at common angles (0, 30, 45, 60, 90 degrees).
• Solution: Memorize the unit circle or learn to derive the values quickly.

6.3. Mixing Up Radian and Degree Measures

Ensure you are using the correct unit of angle measure (radians or degrees).

• Mistake: Using the wrong mode on a calculator.
• Solution: Always check the calculator mode before performing calculations.

6.4. Ignoring the Domain and Range of Trigonometric Functions

Be aware of the domain and range of trigonometric functions.

• Mistake: Expecting a sine or cosine value to be greater than 1 or less than -1.
• Solution: Remember that the range of sine and cosine is [-1, 1].

7. Advanced Trigonometric Concepts

For those looking to deepen their understanding, exploring advanced trigonometric concepts is beneficial.

7.1. Inverse Trigonometric Functions

Inverse trigonometric functions (arcsin, arccos, arctan) are used to find angles from trigonometric ratios.

• arcsin(x): Returns the angle whose sine is x.
• arccos(x): Returns the angle whose cosine is x.
• arctan(x): Returns the angle whose tangent is x.

7.2. Trigonometric Equations

Solving trigonometric equations involves finding the values of angles that satisfy the equation.

• Linear Equations: Use algebraic techniques to isolate the trigonometric function.
• Quadratic Equations: Use factoring or the quadratic formula to solve for the trigonometric function.
• Identities: Use trigonometric identities to simplify the equation.

7.3. Complex Numbers and Trigonometry

Trigonometry is closely related to complex numbers.

• Polar Form: Represent complex numbers in polar form using trigonometric functions.
• De Moivre’s Theorem: Use trigonometry to find powers and roots of complex numbers.

7.4. Hyperbolic Functions

Hyperbolic functions are analogous to trigonometric functions but are defined using hyperbolas instead of circles.

• sinh(x): Hyperbolic sine.
• cosh(x): Hyperbolic cosine.
• tanh(x): Hyperbolic tangent.

8. Resources for Learning Trigonometry

Numerous resources are available to aid in learning trigonometry.

8.1. Online Courses and Tutorials

• Khan Academy: Offers free video lessons and practice exercises on trigonometry.
• Coursera and edX: Provide courses from top universities on trigonometry and related topics.
• YouTube Channels: Many channels offer tutorials and explanations of trigonometric concepts.

8.2. Textbooks and Study Guides

• Schaum’s Outline of Trigonometry: A comprehensive guide with solved problems and practice exercises.
• Trigonometry by Ted Sundstrom and Steven Schlicker: A free online textbook with detailed explanations and examples.
• Precalculus by OpenStax: Covers trigonometry as part of a broader precalculus curriculum.

8.3. Interactive Tools and Software

• Desmos: An online graphing calculator that can be used to visualize trigonometric functions.
• GeoGebra: A dynamic mathematics software for learning and teaching trigonometry.
• Wolfram Alpha: A computational knowledge engine that can solve trigonometric problems and provide step-by-step solutions.

8.4. Mobile Apps

• Photomath: An app that solves math problems by scanning them with a camera.
• Mathway: An app that provides step-by-step solutions to math problems.
• Symbolab: An app that offers a variety of math tools, including a trigonometry solver.

9. Trigonometry and Technology

Technology can significantly enhance the learning and application of trigonometry.

9.1. Graphing Calculators

Graphing calculators are powerful tools for visualizing and analyzing trigonometric functions.

• Plotting Functions: Graph sine, cosine, tangent, and other trigonometric functions to see their behavior.
• Solving Equations: Find solutions to trigonometric equations graphically.
• Analyzing Data: Use trigonometric functions to model and analyze real-world data.

9.2. Computer Algebra Systems (CAS)

CAS software like Mathematica and Maple can perform complex trigonometric calculations and manipulations.

• Symbolic Manipulation: Simplify trigonometric expressions and solve equations symbolically.
• Numerical Computation: Perform numerical calculations with high precision.
• Visualization: Create detailed graphs and animations of trigonometric functions.

9.3. Online Simulators

Online simulators can help visualize trigonometric concepts and explore their properties.

• Unit Circle Simulators: Explore the unit circle and see how trigonometric functions change with angle.
• Wave Simulators: Visualize wave phenomena and see how they are modeled using trigonometric functions.
• Triangle Solvers: Solve triangles by entering known side lengths and angles.

10. Career Paths Involving Trigonometry

Trigonometry is a fundamental tool in many professions.

10.1. Engineering

Engineers use trigonometry in various fields, including:

• Civil Engineering: Designing and analyzing structures like bridges and buildings.
• Mechanical Engineering: Analyzing forces and motion in machines and systems.
• Electrical Engineering: Analyzing signals and circuits.

10.2. Physics

Physicists use trigonometry to model and analyze physical phenomena, including:

• Mechanics: Studying the motion of objects.
• Optics: Analyzing the behavior of light.
• Acoustics: Studying sound waves.

10.3. Architecture

Architects use trigonometry to design and plan buildings.

• Structural Design: Ensuring the stability and safety of buildings.
• Aesthetic Design: Creating visually appealing and functional spaces.
• Surveying and Layout: Accurately measuring and laying out building sites.

10.4. Computer Graphics

Trigonometry is essential for creating realistic and immersive computer graphics.

• 3D Modeling: Creating 3D models of objects and environments.
• Animation: Animating characters and objects.
• Game Development: Developing interactive and engaging games.

11. Trigonometry Tips and Tricks

Here are some additional tips and tricks to make learning trigonometry easier:

11.1. Visualize Problems

Always try to visualize trigonometric problems. Drawing diagrams can help you understand the relationships between angles and sides.

11.2. Use Reference Angles

Reference angles can simplify calculations by reducing angles to the first quadrant.

11.3. Memorize Key Values

Memorize the values of trigonometric functions at key angles (0, 30, 45, 60, 90 degrees) to speed up problem-solving.

11.4. Practice Mental Math

Practice mental math to improve your ability to quickly calculate trigonometric values.

11.5. Review Regularly

Regularly review trigonometric concepts to reinforce your understanding and prevent forgetting.

12. The Historical Significance of Trigonometry

Trigonometry has a rich history dating back to ancient civilizations.

12.1. Ancient Civilizations

• Egyptians: Used trigonometry for surveying and construction.
• Babylonians: Developed early trigonometric tables for astronomical calculations.
• Greeks: Made significant contributions to trigonometry, including the development of trigonometric functions.

12.2. Medieval Scholars

• Islamic Scholars: Preserved and expanded upon Greek knowledge of trigonometry.
• Indian Mathematicians: Developed sine and cosine functions and made advancements in spherical trigonometry.

12.3. Renaissance and Beyond

• European Mathematicians: Further developed trigonometry and applied it to navigation, astronomy, and physics.
• Modern Applications: Trigonometry continues to be essential in various fields, including engineering, science, and technology.

13. Making Trigonometry Fun and Engaging

Learning trigonometry doesn’t have to be a chore. Here are some ways to make it fun and engaging:

13.1. Use Real-World Examples

Connect trigonometry to real-world situations that interest you. For example, use trigonometry to calculate the height of a building or the distance to a star.

13.2. Solve Puzzles and Games

Solve trigonometric puzzles and games to make learning more interactive.

13.3. Work with Others

Study with friends or join a math club to make learning more social and collaborative.

13.4. Take Breaks

Take regular breaks to avoid burnout and stay focused.

13.5. Reward Yourself

Reward yourself for achieving milestones in your trigonometry studies.

14. Common Trigonometry Challenges and Solutions

Addressing common challenges can help you overcome difficulties in learning trigonometry.

14.1. Understanding Abstract Concepts

• Challenge: Difficulty grasping abstract trigonometric concepts.
• Solution: Use visual aids, real-world examples, and hands-on activities to make concepts more concrete.

14.2. Memorizing Formulas

• Challenge: Difficulty memorizing trigonometric formulas.
• Solution: Use mnemonics, flashcards, and regular practice to reinforce memory.

14.3. Solving Complex Problems

• Challenge: Difficulty solving complex trigonometric problems.
• Solution: Break problems down into smaller steps, use diagrams, and seek help from teachers or tutors.

14.4. Staying Motivated

• Challenge: Losing motivation to study trigonometry.
• Solution: Set realistic goals, reward yourself for progress, and connect trigonometry to your interests.

15. Staying Up-To-Date with Trigonometry

Trigonometry, while a classical field, continues to evolve with new applications and techniques.

15.1. Emerging Applications

• Quantum Computing: Trigonometry plays a role in quantum algorithms.
• Data Science: Trigonometric functions are used in signal processing and time series analysis.
• Virtual Reality: Trigonometry is essential for creating immersive VR environments.

15.2. New Learning Tools

• Adaptive Learning Platforms: Platforms that tailor learning to individual needs and progress.
• Augmented Reality Apps: Apps that use AR to visualize trigonometric concepts in the real world.

15.3. Advanced Research

• Publications and Journals: Stay updated with the latest research in trigonometry through academic publications and journals.
• Conferences and Workshops: Attend conferences and workshops to learn from experts and network with peers.

16. Understanding Trigonometry Through Analogies

Analogies can make trigonometry concepts easier to understand by relating them to familiar ideas.

16.1. Trigonometry as Anatomy

Imagine studying human anatomy. Just as biologists label bones and muscles, trigonometry labels the parts of triangles. These labels (sine, cosine, tangent) help us understand the relationships within triangles and, by extension, circles and cycles.

16.2. The Dome, Wall, and Ceiling Analogy

Visualize a dome, a wall, and a ceiling to understand trigonometric functions.

• Dome: Sine and cosine relate to the height and distance within the dome.
• Wall: Tangent and secant relate to the height and distance on the wall.
• Ceiling: Cotangent and cosecant relate to the distance along the ceiling and the ramp to reach it.

16.3. Percentages

Trigonometric values can be understood as percentages.

• Sine and Cosine: Represent percentages of the maximum height or distance within the unit circle.
• Tangent: Represents the height of a screen on a wall as a percentage of the distance to the wall.

17. Key Trigonometry Concepts in Table Format

To summarize, here are key trigonometry concepts in a table format for quick reference:

Concept	Definition	Formula
Sine (sin)	Ratio of opposite side to hypotenuse in a right triangle	$sin(theta) = frac{text{Opposite}}{text{Hypotenuse}}$
Cosine (cos)	Ratio of adjacent side to hypotenuse in a right triangle	$cos(theta) = frac{text{Adjacent}}{text{Hypotenuse}}$
Tangent (tan)	Ratio of opposite side to adjacent side in a right triangle	$tan(theta) = frac{text{Opposite}}{text{Adjacent}}$
Unit Circle	Circle with radius 1 used to visualize trigonometric functions	$x^2 + y^2 = 1$, where $x = cos(theta)$ and $y = sin(theta)$
Pythagorean Identity	Fundamental identity relating sine and cosine	$sin^2(theta) + cos^2(theta) = 1$
Law of Sines	Relates sides of a triangle to sines of opposite angles	$frac{a}{sin(A)} = frac{b}{sin(B)} = frac{c}{sin(C)}$
Law of Cosines	Relates sides and angles in any triangle	$c^2 = a^2 + b^2 – 2abcos(C)$
Reciprocal Identities	Relationships between trigonometric functions	$csc(theta) = frac{1}{sin(theta)}$, $sec(theta) = frac{1}{cos(theta)}$, $cot(theta) = frac{1}{tan(theta)}$
Angle Sum Formulas	Formulas for trigonometric functions of sums of angles	$sin(A+B) = sin(A)cos(B) + cos(A)sin(B)$, $cos(A+B) = cos(A)cos(B) – sin(A)sin(B)$
Double Angle Formulas	Formulas for trigonometric functions of double angles	$sin(2theta) = 2sin(theta)cos(theta)$, $cos(2theta) = cos^2(theta) – sin^2(theta)$
Half Angle Formulas	Formulas for trigonometric functions of half angles	$sin(frac{theta}{2}) = pm sqrt{frac{1 – cos(theta)}{2}}$, $cos(frac{theta}{2}) = pm sqrt{frac{1 + cos(theta)}{2}}$

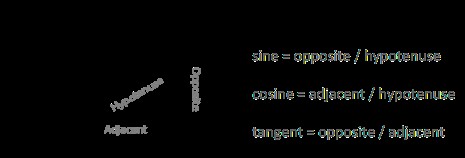
18. Advanced Trigonometry Applications in Modern Technologies

Modern technologies are increasingly reliant on advanced trigonometry applications, expanding its relevance beyond traditional fields.

18.1. Robotics and Automation

• Kinematics: Trigonometry is used to calculate the movements and positions of robotic arms.
• Navigation: Autonomous robots rely on trigonometric functions for path planning and obstacle avoidance.
• Machine Vision: Object recognition and tracking use trigonometric principles to interpret visual data.

18.2. Aerospace Engineering

• Trajectory Calculation: Trigonometry is essential for calculating the trajectories of spacecraft and aircraft.
• Satellite Positioning: Determining the positions of satellites and their orientations in space relies on trigonometric functions.
• Control Systems: Maintaining stability and control of aerospace vehicles uses trigonometric models.

18.3. Medical Imaging

• CT Scans: Trigonometric transformations are used to reconstruct images from CT scan data.
• MRI: Magnetic Resonance Imaging utilizes trigonometric functions to analyze and interpret magnetic fields.
• Ultrasound: Trigonometry is used to process and display ultrasound images.

18.4. Meteorology

• Weather Forecasting: Trigonometric models are used to analyze weather patterns and predict future weather conditions.
• Climate Modeling: Understanding climate change and its impacts involves complex trigonometric calculations.

19. Trigonometry Practice Problems with Solutions

To solidify your understanding, here are some practice problems with detailed solutions:

19.1. Problem 1

A ladder leans against a wall, making an angle of 60 degrees with the ground. If the foot of the ladder is 5 feet away from the wall, how high does the ladder reach on the wall?

Solution:

1. Identify: We have a right triangle with the angle between the ground and the ladder being 60 degrees. The distance from the wall to the foot of the ladder is the adjacent side (5 feet). We need to find the opposite side, which is the height the ladder reaches on the wall.
2. Choose: Use the tangent function: $tan(theta) = frac{text{Opposite}}{text{Adjacent}}$.
3. Set Up: $tan(60^circ) = frac{text{Height}}{5}$.
4. Solve: $text{Height} = 5 times tan(60^circ) = 5 times sqrt{3} approx 8.66$ feet.
5. Check: The height the ladder reaches on the wall is approximately 8.66 feet.

19.2. Problem 2

A boat is sailing towards a lighthouse. At a certain point, the angle of elevation to the top of the lighthouse is 30 degrees. After the boat sails 100 meters closer, the angle of elevation is 45 degrees. If the lighthouse is on a cliff 20 meters high, what is the height of the lighthouse above sea level?

Solution:

1. Identify: Let $h$ be the height of the lighthouse above the cliff. Let $d$ be the initial distance from the boat to the base of the lighthouse.
2. Choose: We have two right triangles. Use the tangent function.
3. Set Up:
   • $tan(30^circ) = frac{h + 20}{d}$
   • $tan(45^circ) = frac{h + 20}{d – 100}$
4. Solve:
   • $d = frac{h + 20}{tan(30^circ)}$
   • $d – 100 = frac{h + 20}{tan(45^circ)}$
   • Substitute $d$: $frac{h + 20}{tan(30^circ)} – 100 = frac{h + 20}{tan(45^circ)}$
   • Solve for $h$: $h approx 116.6$ meters.
5. Check: The height of the lighthouse above sea level is $h + 20 approx 136.6$ meters.

19.3. Problem 3

Simplify the expression: $frac{sin(2x)}{sin(x)}$.

Solution:

1. Identify: We need to simplify a trigonometric expression.
2. Choose: Use the double angle formula for sine: $sin(2x) = 2sin(x)cos(x)$.
3. Set Up: $frac{2sin(x)cos(x)}{sin(x)}$.
4. Solve: Cancel out $sin(x)$: $2cos(x)$.
5. Check: The simplified expression is $2cos(x)$.

20. Frequently Asked Questions (FAQs) About Trigonometry

20.1. What is trigonometry used for?

Trigonometry is used in various fields, including engineering, physics, architecture, navigation, and computer graphics. It helps solve problems involving angles, distances, and shapes.

20.2. How can I remember trigonometric ratios?

Use the mnemonic SOH-CAH-TOA: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.

20.3. What is the unit circle?

The unit circle is a circle with a radius of 1, centered at the origin, used to visualize trigonometric functions and their values at different angles.

20.4. How do I solve trigonometric equations?

Use algebraic techniques, trigonometric identities, and the unit circle to find the values of angles that satisfy the equation.

20.5. What are the basic trigonometric identities?

The basic identities include reciprocal identities, quotient identities, and Pythagorean identities.

20.6. How do I use a calculator for trigonometry?

Ensure the calculator is in the correct mode (degrees or radians) and use the appropriate trigonometric functions (sin, cos, tan) and their inverses.

20.7. What is the Law of Sines and Law of Cosines?

The Law of Sines relates the sides of a triangle to the sines of their opposite angles, while the Law of Cosines relates the sides and angles in any triangle.

20.8. How can I improve my trigonometry skills?

Practice regularly, use visual aids, seek help from teachers or tutors, and apply trigonometry to real-world scenarios.

20.9. What are inverse trigonometric functions?

Inverse trigonometric functions (arcsin, arccos, arctan) are used to find the angles corresponding to given trigonometric ratios.

20.10. Where can I find reliable resources for learning trigonometry?

Online courses, textbooks, interactive tools, and mobile apps are excellent resources for learning trigonometry.

Learning trigonometry can be significantly easier with the right approach and resources. By understanding the fundamentals, visualizing trigonometric functions, adopting effective learning strategies, and practicing regularly, you can master trigonometry.

If you’re looking to further enhance your understanding and skills in trigonometry, visit LEARNS.EDU.VN for more detailed articles, courses, and expert guidance. Explore our resources and unlock your potential in mathematics!

Contact Information:

• Address: 123 Education Way, Learnville, CA 90210, United States
• WhatsApp: +1 555-555-1212
• Website: learns.edu.vn