Mean-field games (MFGs) and mean-field control (MFC) are powerful tools for analyzing large populations of interacting agents. Traditionally, numerical solutions for these problems have relied on mesh-based methods, suffering from the curse of dimensionality. This article presents a novel approach using A Mean-field Optimal Control Formulation Of Deep Learning, leveraging Lagrangian PDE solvers and neural networks to overcome this limitation. This mesh-free method offers a scalable and efficient solution for high-dimensional MFG and MFC problems, opening doors to previously intractable applications.
Recent advances in machine learning have enabled the development of novel numerical methods for solving high-dimensional partial differential equations (PDEs) and control problems. This article explores a mesh-free framework that combines Lagrangian PDE solvers with neural networks to tackle the curse of dimensionality in mean-field games (MFGs) and mean-field control (MFC). By penalizing violations of the underlying Hamilton-Jacobi-Bellman (HJB) equation, this method achieves increased accuracy and computational efficiency, transforming complex MFGs into tractable machine learning problems.
The Challenge of High-Dimensional MFGs and MFCs
MFGs and MFCs provide a framework for modeling complex systems with a large number of interacting agents. Applications range from economics and finance to crowd motion and data science. However, solving these problems numerically, especially in high-dimensional spaces, presents significant challenges. Traditional methods often rely on spatial discretization, leading to exponential growth in computational complexity as the dimensionality increases.
A Lagrangian Perspective with Neural Networks
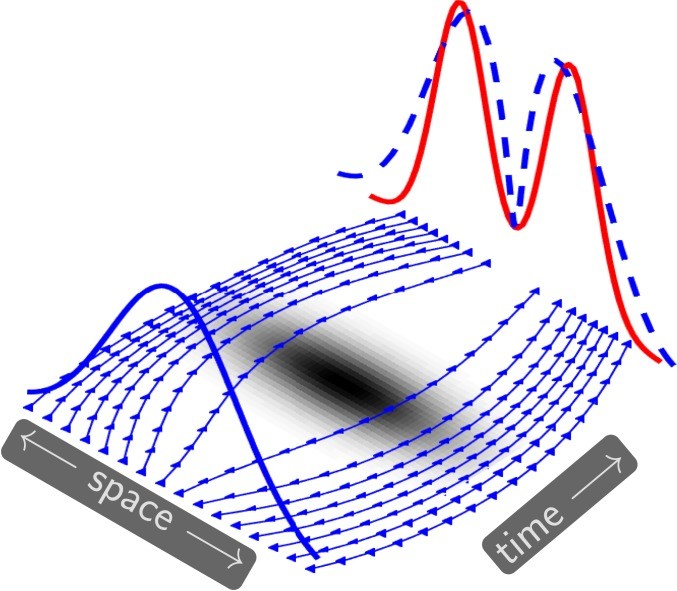
This novel approach addresses the curse of dimensionality by adopting a Lagrangian perspective. The continuity equation, a key component of MFGs, is solved using characteristic curves, eliminating the need for explicit density representation. Furthermore, the value function, central to the solution of MFGs and MFCs, is parameterized using a specifically designed neural network.
This neural network architecture facilitates accurate and efficient approximation of the characteristic curves and allows for direct penalization of HJB equation violations during training. This ensures that the learned solution adheres to the optimality conditions of the problem. The Lagrangian formulation, combined with the neural network parameterization, results in a mesh-free and highly parallelizable numerical scheme.
Penalizing HJB Violations for Enhanced Accuracy
A key innovation of this framework is the incorporation of a penalty term for deviations from the HJB equation. This penalty, integrated into the training process, encourages the neural network to learn a solution that satisfies the optimality conditions more accurately. Numerical experiments demonstrate that this penalty significantly improves convergence and solution quality.
Scaling to High Dimensions: Numerical Results
The effectiveness of this method is showcased through numerical experiments on high-dimensional instances of optimal transport (OT) and crowd motion problems. Results demonstrate the ability to solve problems with up to 100 spatial dimensions on standard computational resources. The method’s accuracy is validated by comparison with a traditional Eulerian solver in two dimensions.
Conclusion: A Promising Direction for MFG and MFC Research
This mean-field optimal control formulation of deep learning offers a significant advancement in the numerical solution of MFGs and MFCs. By leveraging Lagrangian methods and neural networks, this mesh-free approach overcomes the curse of dimensionality, enabling the solution of high-dimensional problems that were previously intractable. This framework not only provides a powerful tool for tackling existing challenges but also opens exciting new avenues for research at the intersection of machine learning, PDEs, and optimal control. Future work will focus on refining the neural network architectures, exploring different penalty functions, and applying this methodology to a broader range of real-world problems.