Diffusion Model Manifold Learning: A Comprehensive Guide

Diffusion Model Manifold Learning represents a cutting-edge area in machine learning, offering powerful techniques for data generation and representation. At LEARNS.EDU.VN, we’re dedicated to demystifying complex topics and providing accessible knowledge for learners of all levels. This article will delve into the intricacies of diffusion models and their application in manifold learning, offering a clear understanding of the underlying principles and practical implementations. This comprehensive guide also covers probabilistic models and generative models, as well as manifold representations.

1. Understanding Diffusion Models

Diffusion models are a class of generative models that have recently gained significant attention due to their ability to generate high-quality samples, particularly in image synthesis. These models are inspired by non-equilibrium thermodynamics and leverage the concept of gradually adding noise to data and then learning to reverse this process to generate new samples. Let’s explore the key components and principles behind diffusion models.

1.1. The Forward Diffusion Process

The forward diffusion process, also known as the noising process, involves gradually adding Gaussian noise to the data over a series of timesteps. This process transforms the original data distribution into a simple, tractable distribution, typically a Gaussian distribution. The forward process can be defined as follows:

q(x1:T|x0) = ∏ t=1 T q(xt|xt-1)

where:

• x0 represents the original data sample.
• x1:T represents the sequence of noisy samples from timestep 1 to T.
• q(xt|xt-1) is the conditional probability distribution of xt given xt-1, which is a Gaussian distribution with mean determined by xt-1 and a variance schedule βt.

The variance schedule β1, …, βT controls the amount of noise added at each timestep. As t increases, the data becomes increasingly noisy, eventually converging to a pure Gaussian distribution at timestep T.

1.2. The Reverse Diffusion Process

The reverse diffusion process, also known as the denoising process, is the core of the diffusion model. It involves learning to reverse the forward process, i.e., learning to gradually remove noise from a noisy sample to generate a new sample. The reverse process is also modeled as a Markov chain:

pθ(x0:T) = p(xT) ∏ t=1 T pθ(xt-1|xt)

where:

• p(xT) is the Gaussian distribution representing the pure noise at timestep T.
• pθ(xt-1|xt) is the conditional probability distribution of xt-1 given xt, which is a Gaussian distribution with mean and variance learned by the model.

The model learns the parameters of the reverse process by training on the training data. The goal is to minimize the difference between the generated samples and the real data samples.

1.3. Training Diffusion Models

Diffusion models are trained by minimizing a loss function that measures the difference between the generated samples and the real data samples. A common loss function is the variational lower bound (VLB) on the negative log-likelihood of the data:

L = Et[||ε – εθ(xt, t)||^2]

where:

• ε is the noise added to the data at timestep t.
• εθ(xt, t) is the noise predicted by the model at timestep t.

The model is trained to predict the noise added to the data at each timestep. By accurately predicting the noise, the model can effectively reverse the diffusion process and generate high-quality samples.

**1.4. Advantages of Diffusion Models

Diffusion models offer several advantages over other generative models, such as GANs (Generative Adversarial Networks) and VAEs (Variational Autoencoders):

• High-Quality Samples: Diffusion models are capable of generating high-quality samples that are often indistinguishable from real data.
• Stable Training: Diffusion models are known for their stable training process, which is less prone to mode collapse and other training issues that can plague GANs.
• Theoretical Foundation: Diffusion models are grounded in a solid theoretical foundation based on non-equilibrium thermodynamics and stochastic processes.
• Flexibility: Diffusion models can be applied to a wide range of data types, including images, audio, and text.

2. Manifold Learning: Unveiling Hidden Structures

Manifold learning is a class of techniques that aim to discover the underlying low-dimensional manifold structure of high-dimensional data. In many real-world datasets, the data points are not uniformly distributed in the high-dimensional space but rather lie on or near a lower-dimensional manifold. Manifold learning algorithms seek to uncover this hidden structure, which can be useful for various tasks such as data visualization, dimensionality reduction, and data generation. Let’s delve into the core concepts and methods of manifold learning.

2.1. What is a Manifold?

In mathematics, a manifold is a topological space that locally resembles Euclidean space. Informally, this means that a manifold is a space that looks like a flat plane when you zoom in close enough. Examples of manifolds include:

• A line (1-dimensional manifold)
• A plane (2-dimensional manifold)
• A sphere (2-dimensional manifold embedded in 3-dimensional space)
• A torus (2-dimensional manifold embedded in 3-dimensional space)

In the context of machine learning, a manifold is often used to describe the underlying structure of a dataset. For example, a dataset of images of faces may lie on a lower-dimensional manifold in the high-dimensional space of all possible images.

2.2. Why Manifold Learning?

Manifold learning offers several benefits:

• Dimensionality Reduction: Manifold learning can reduce the dimensionality of the data while preserving its essential structure. This can be useful for simplifying data analysis and visualization.
• Data Visualization: Manifold learning can be used to project high-dimensional data onto a lower-dimensional space, making it easier to visualize and understand the data.
• Data Generation: Manifold learning can be used to generate new data points that lie on the same manifold as the original data. This can be useful for data augmentation and generative modeling.
• Feature Extraction: Manifold learning can be used to extract meaningful features from the data that capture the underlying structure of the manifold.

2.3. Manifold Learning Techniques

Several manifold learning techniques have been developed over the years. Some of the most popular techniques include:

• Principal Component Analysis (PCA): PCA is a linear dimensionality reduction technique that projects the data onto the principal components, which are the directions of maximum variance in the data.
• Isometric Mapping (Isomap): Isomap is a nonlinear dimensionality reduction technique that preserves the geodesic distances between data points, i.e., the distances measured along the manifold.
• Locally Linear Embedding (LLE): LLE is a nonlinear dimensionality reduction technique that preserves the local linear relationships between data points.
• t-Distributed Stochastic Neighbor Embedding (t-SNE): t-SNE is a nonlinear dimensionality reduction technique that is particularly well-suited for visualizing high-dimensional data in low-dimensional space.
• Uniform Manifold Approximation and Projection (UMAP): UMAP is a nonlinear dimensionality reduction technique that preserves both the local and global structure of the data.

2.4. Considerations for Manifold Learning Selection

Choosing the right manifold learning technique depends on the specific dataset and the goals of the analysis. Some factors to consider include:

• Linearity vs. Nonlinearity: If the data is linearly separable, then a linear technique like PCA may be sufficient. If the data is nonlinear, then a nonlinear technique like Isomap, LLE, t-SNE, or UMAP is needed.
• Global vs. Local Structure: Some techniques, like Isomap and UMAP, aim to preserve the global structure of the data, while others, like LLE and t-SNE, focus on preserving the local structure.
• Computational Cost: Some techniques, like t-SNE, can be computationally expensive, especially for large datasets.

3. Diffusion Model Manifold Learning: Bridging the Gap

Diffusion Model Manifold Learning combines the strengths of diffusion models and manifold learning to achieve powerful data generation and representation capabilities. By leveraging the ability of diffusion models to generate high-quality samples and the ability of manifold learning to uncover the underlying structure of data, Diffusion Model Manifold Learning offers a promising approach for various machine-learning tasks.

3.1. The Core Idea

The core idea behind Diffusion Model Manifold Learning is to train a diffusion model on data that lies on or near a low-dimensional manifold. By doing so, the diffusion model learns to generate new samples that also lie on or near the same manifold. This approach offers several advantages:

• Improved Sample Quality: By constraining the generated samples to lie on a manifold, the diffusion model can generate higher-quality samples that are more realistic and coherent.
• Reduced Dimensionality: By learning a representation of the data on a manifold, the diffusion model can reduce the dimensionality of the data while preserving its essential structure.
• Enhanced Data Understanding: By uncovering the underlying manifold structure of the data, the diffusion model can provide insights into the relationships between data points and the underlying factors that generate the data.

3.2. Approaches to Diffusion Model Manifold Learning

Several approaches have been proposed for Diffusion Model Manifold Learning. Some of the most common approaches include:

• Manifold Regularization: This approach involves adding a regularization term to the diffusion model’s loss function that encourages the generated samples to lie on or near a known manifold. The manifold can be defined using various techniques, such as PCA, Isomap, or LLE.
• Manifold Projection: This approach involves projecting the noisy samples generated during the forward diffusion process onto a known manifold. This ensures that the reverse diffusion process starts from a point on the manifold, which can improve the quality of the generated samples.
• Latent Space Manifold Learning: This approach involves learning a manifold structure in the latent space of the diffusion model. This allows the diffusion model to generate samples by traversing the manifold in the latent space, which can produce more diverse and coherent samples.

3.3. Applications of Diffusion Model Manifold Learning

Diffusion Model Manifold Learning has a wide range of applications, including:

• Image Generation: Diffusion Model Manifold Learning can be used to generate high-quality images of faces, objects, and scenes.
• Audio Synthesis: Diffusion Model Manifold Learning can be used to synthesize realistic audio signals, such as speech and music.
• Data Augmentation: Diffusion Model Manifold Learning can be used to augment datasets by generating new samples that lie on the same manifold as the original data.
• Anomaly Detection: Diffusion Model Manifold Learning can be used to detect anomalies by identifying data points that lie far from the learned manifold.

4. Practical Implementation of Diffusion Model Manifold Learning

Implementing Diffusion Model Manifold Learning involves several steps, from data preparation to model training and evaluation. Here’s a practical guide to help you get started.

4.1. Data Preparation

The first step is to prepare your data. This involves:

• Data Collection: Gather the data you want to use for training. This could be images, audio, or any other type of data.
• Data Preprocessing: Preprocess the data to ensure it is in a suitable format for training. This may involve resizing images, normalizing audio signals, or converting text to numerical representations.
• Manifold Estimation: Estimate the underlying manifold structure of the data using a manifold learning technique such as PCA, Isomap, LLE, t-SNE, or UMAP.

4.2. Model Architecture

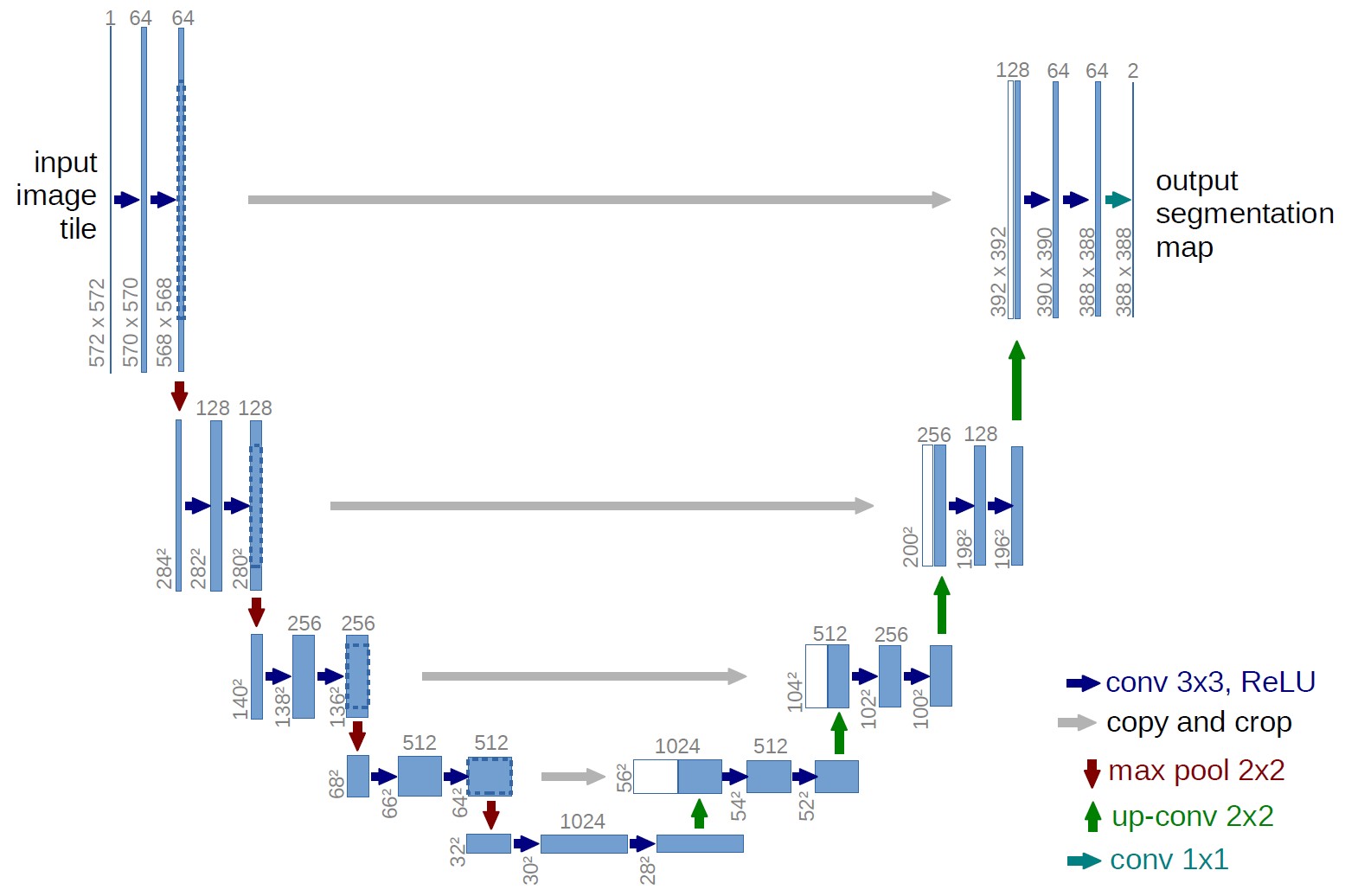
Choose a suitable model architecture for your diffusion model. A common choice is a U-Net-like architecture, which has been shown to be effective for image generation tasks. The model should be able to:

• Encode the data: Map the input data to a latent space.
• Perform the forward diffusion process: Gradually add noise to the data in the latent space.
• Learn the reverse diffusion process: Gradually remove noise from the noisy data to generate new samples.
• Decode the data: Map the latent representation back to the original data space.

4.3. Training the Model

Train the diffusion model using a suitable loss function and optimization algorithm. The loss function should measure the difference between the generated samples and the real data samples. Common loss functions include the variational lower bound (VLB) and the mean squared error (MSE). The optimization algorithm should be able to efficiently minimize the loss function. Common optimization algorithms include Adam and SGD. The training process should involve:

• Forward Pass: Pass the data through the forward diffusion process to generate noisy samples.
• Reverse Pass: Pass the noisy samples through the reverse diffusion process to generate new samples.
• Loss Calculation: Calculate the loss between the generated samples and the real data samples.
• Parameter Update: Update the model parameters based on the calculated loss.

4.4. Evaluation

Evaluate the performance of the diffusion model using suitable metrics. Common metrics include:

• Fréchet Inception Distance (FID): FID measures the similarity between the generated samples and the real data samples in terms of their Inception features.
• Structural Similarity Index (SSIM): SSIM measures the structural similarity between the generated samples and the real data samples.
• Perceptual Quality: Assess the perceptual quality of the generated samples using human evaluators.

5. Advanced Concepts in Diffusion Model Manifold Learning

To further enhance your understanding of Diffusion Model Manifold Learning, let’s explore some advanced concepts and techniques.

5.1. Conditional Diffusion Models

Conditional diffusion models allow you to control the generation process by conditioning the model on additional information, such as class labels, text descriptions, or other modalities. This can be useful for generating specific types of data or for controlling the attributes of the generated samples.

5.2. Hierarchical Diffusion Models

Hierarchical diffusion models involve training multiple diffusion models at different levels of abstraction. This allows the model to capture both the global structure and the local details of the data.

5.3. Diffusion Transformers

Diffusion Transformers combine the strengths of diffusion models and Transformers, a powerful class of neural networks that have achieved state-of-the-art results in natural language processing and computer vision. Diffusion Transformers can be used to generate high-quality samples with long-range dependencies.

5.4. Current Trends and Research Directions

Diffusion Model Manifold Learning is a rapidly evolving field, with new research and developments emerging constantly. Some current trends and research directions include:

• Improving Sample Quality: Researchers are constantly working on improving the quality of the samples generated by diffusion models.
• Reducing Computational Cost: Diffusion models can be computationally expensive to train and sample from. Researchers are exploring techniques to reduce the computational cost of diffusion models.
• Exploring New Applications: Researchers are exploring new applications of diffusion models in various fields, such as drug discovery, materials science, and robotics.

6. Case Studies: Real-World Applications

Let’s examine some real-world case studies that showcase the power and versatility of Diffusion Model Manifold Learning.

6.1. Image Super-Resolution

Diffusion Model Manifold Learning has been used to achieve state-of-the-art results in image super-resolution, the task of increasing the resolution of an image. By training a diffusion model on high-resolution images and conditioning it on low-resolution images, the model can generate high-resolution images that are both realistic and faithful to the original low-resolution images.

6.2. Image Inpainting

Diffusion Model Manifold Learning has also been used for image inpainting, the task of filling in missing or corrupted regions of an image. By training a diffusion model on complete images and conditioning it on the known regions of the image, the model can generate realistic and coherent content to fill in the missing regions.

6.3. Anomaly Detection in Medical Images

Diffusion Model Manifold Learning can be used for anomaly detection in medical images, such as X-rays and MRIs. By training a diffusion model on healthy images and identifying images that deviate significantly from the learned manifold, it is possible to detect anomalies that may indicate disease or injury.

7. Tools and Resources for Diffusion Model Manifold Learning

To help you get started with Diffusion Model Manifold Learning, here are some useful tools and resources:

Tool/Resource	Description
PyTorch	A popular deep learning framework that provides the necessary tools and libraries for implementing diffusion models and manifold learning algorithms.
TensorFlow	Another popular deep learning framework that can be used for implementing diffusion models and manifold learning algorithms.
denoising-diffusion-pytorch	A PyTorch package that implements an image diffusion model, making it easy to train and generate images.
Scikit-learn	A Python library that provides a wide range of manifold learning algorithms, such as PCA, Isomap, LLE, t-SNE, and UMAP.
Research Papers	Stay up-to-date with the latest research in Diffusion Model Manifold Learning by reading papers on arXiv and other academic databases.
Online Courses and Tutorials	Explore online courses and tutorials on platforms like Coursera, edX, and YouTube to learn more about diffusion models and manifold learning.
LEARNS.EDU.VN	Visit LEARNS.EDU.VN for more articles, tutorials, and resources on machine learning and artificial intelligence.

8. The Future of Diffusion Model Manifold Learning

Diffusion Model Manifold Learning is a rapidly evolving field with a bright future. As research progresses and new techniques are developed, we can expect to see even more powerful and versatile applications of Diffusion Model Manifold Learning in various domains. Some potential future directions include:

• Generative Modeling for Scientific Discovery: Diffusion Model Manifold Learning could be used to generate new molecules, materials, and designs with desired properties, accelerating scientific discovery.
• Creative Content Generation: Diffusion Model Manifold Learning could be used to generate new forms of art, music, and literature, pushing the boundaries of creativity.
• Personalized Healthcare: Diffusion Model Manifold Learning could be used to generate personalized medical images and treatment plans, improving patient outcomes.
• Robotics and Automation: Diffusion Model Manifold Learning could be used to train robots to perform complex tasks in unstructured environments.

9. Addressing Common Challenges

While Diffusion Model Manifold Learning holds immense potential, it also presents several challenges. Understanding these challenges and exploring potential solutions is crucial for advancing the field.

9.1. Computational Complexity

Training and sampling from diffusion models can be computationally expensive, especially for high-dimensional data. This limits their applicability to large-scale datasets and real-time applications.

Potential Solutions:

• Model Compression Techniques: Explore model compression techniques such as pruning, quantization, and knowledge distillation to reduce the size and complexity of diffusion models without sacrificing performance.
• Efficient Sampling Algorithms: Develop more efficient sampling algorithms that can generate high-quality samples with fewer iterations.
• Hardware Acceleration: Leverage specialized hardware such as GPUs and TPUs to accelerate the training and sampling processes.

9.2. Mode Collapse and Lack of Diversity

Diffusion models can sometimes suffer from mode collapse, where the model only generates a limited set of samples, lacking diversity. This can be a problem for applications that require a wide range of outputs.

Potential Solutions:

• Regularization Techniques: Employ regularization techniques such as dropout, weight decay, and spectral normalization to prevent overfitting and encourage the model to explore a wider range of modes.
• Adversarial Training: Incorporate adversarial training to encourage the model to generate more diverse and realistic samples.
• Manifold Regularization: Regularize the model to generate samples that lie on or near a diverse set of manifolds, promoting exploration of different data modes.

9.3. Interpretability and Explainability

Diffusion models are often considered black boxes, making it difficult to understand why they generate certain outputs. This lack of interpretability can be a barrier to adoption in critical applications where transparency and accountability are essential.

Potential Solutions:

• Visualization Techniques: Develop visualization techniques to explore the latent space of diffusion models and understand how different regions of the space correspond to different data features.
• Attention Mechanisms: Incorporate attention mechanisms to identify the parts of the input data that are most relevant to the generated output.
• Explainable AI (XAI) Methods: Apply XAI methods to explain the decisions made by diffusion models and provide insights into their inner workings.

10. Frequently Asked Questions (FAQ)

Here are some frequently asked questions about Diffusion Model Manifold Learning:

1. What are diffusion models?
   Diffusion models are generative models that learn to generate data by reversing a process of gradually adding noise to the data.
2. What is manifold learning?
   Manifold learning is a class of techniques that aim to discover the underlying low-dimensional manifold structure of high-dimensional data.
3. What is Diffusion Model Manifold Learning?
   Diffusion Model Manifold Learning combines the strengths of diffusion models and manifold learning to achieve powerful data generation and representation capabilities.
4. What are the advantages of Diffusion Model Manifold Learning?
   Improved sample quality, reduced dimensionality, and enhanced data understanding.
5. What are some applications of Diffusion Model Manifold Learning?
   Image generation, audio synthesis, data augmentation, and anomaly detection.
6. What are some challenges of Diffusion Model Manifold Learning?
   Computational complexity, mode collapse, and lack of interpretability.
7. What tools and resources can I use to get started with Diffusion Model Manifold Learning?
   PyTorch, TensorFlow, scikit-learn, and online courses and tutorials.
8. What are some future directions in Diffusion Model Manifold Learning?
   Generative modeling for scientific discovery, creative content generation, personalized healthcare, and robotics and automation.
9. How does manifold regularization improve diffusion models?
   It encourages generated samples to lie on or near a known manifold, enhancing sample quality and coherence.
10. Can diffusion models be used for data augmentation?
    Yes, by generating new samples that lie on the same manifold as the original data.

Conclusion

Diffusion Model Manifold Learning is a powerful and versatile technique that offers promising solutions for various machine-learning tasks. By combining the strengths of diffusion models and manifold learning, this approach can generate high-quality samples, reduce dimensionality, and enhance data understanding. As research progresses and new techniques are developed, we can expect to see even more exciting applications of Diffusion Model Manifold Learning in the years to come.

Ready to explore the fascinating world of machine learning? Visit learns.edu.vn to discover more articles, tutorials, and courses that will help you unlock your potential and achieve your learning goals. Contact us at 123 Education Way, Learnville, CA 90210, United States, or via WhatsApp at +1 555-555-1212.