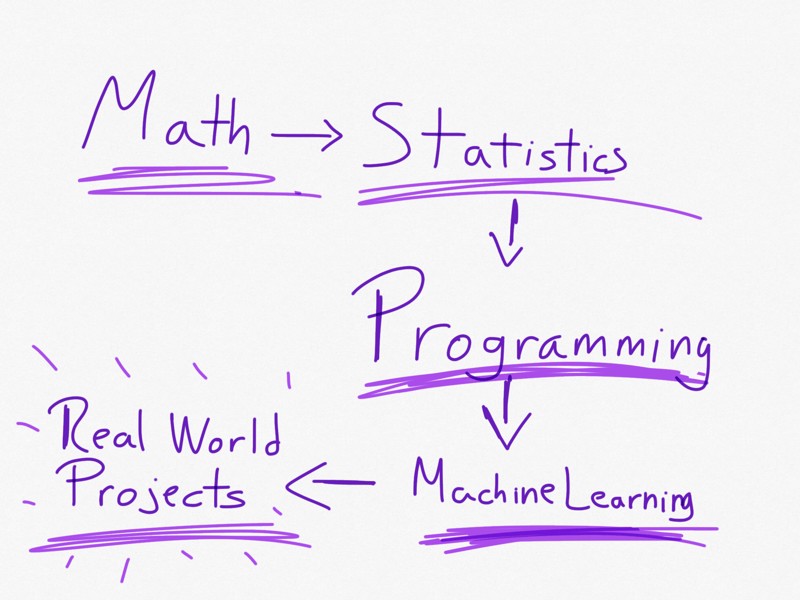
Do You Need Math For Machine Learning? Absolutely! Math is the bedrock of machine learning, providing the essential tools and concepts to understand and build intelligent systems. At LEARNS.EDU.VN, we help you navigate the mathematical landscape, ensuring you’re well-equipped for your machine learning journey. Let’s explore the key mathematical areas and how they empower you to excel in this exciting field, turning complex equations into practical applications. Our comprehensive resources ensure a solid foundation in calculus, linear algebra, and statistics, paving the way for success in machine learning algorithms and data analysis.
1. Understanding the Role of Math in Machine Learning
Machine learning (ML) involves creating algorithms that enable computers to learn from data without explicit programming. Math provides the language and tools to formulate, analyze, and optimize these algorithms. Whether you’re building predictive models, clustering data, or designing neural networks, math is indispensable. Without a solid mathematical foundation, understanding the inner workings of ML models and their limitations becomes a daunting task.
1.1. Why Math Matters in Machine Learning
Math is fundamental to machine learning because it allows you to:
- Formulate Problems Precisely: Translate real-world problems into mathematical models that ML algorithms can solve.
- Understand Algorithms: Grasp the underlying principles of algorithms like linear regression, logistic regression, and support vector machines.
- Optimize Models: Use calculus and optimization techniques to fine-tune model parameters for better performance.
- Evaluate Performance: Apply statistical methods to assess model accuracy and reliability.
- Interpret Results: Make sense of model outputs and draw meaningful conclusions.
1.2. Foundational Math Concepts for Machine Learning
Several key mathematical areas are crucial for machine learning:
- Linear Algebra: Deals with vectors, matrices, and linear transformations, essential for representing data and performing computations in ML models.
- Calculus: Provides tools for optimization, gradient descent, and understanding the behavior of functions, vital for training ML algorithms.
- Probability and Statistics: Enables you to model uncertainty, analyze data distributions, and evaluate model performance.
- Discrete Math: Important for certain ML applications, such as graph-based models and combinatorial optimization.
2. Essential Math Topics for Machine Learning
Let’s delve deeper into the specific math topics you’ll need to master for a successful machine-learning career.
2.1. Linear Algebra
Linear algebra is the math of vectors and matrices. It provides the foundation for representing data, performing transformations, and solving systems of equations, all of which are central to machine learning.
2.1.1. Key Concepts in Linear Algebra
- Vectors and Matrices: Understanding how to represent data points and datasets using vectors and matrices.
- Matrix Operations: Performing operations like addition, subtraction, multiplication, and transposition.
- Eigenvalues and Eigenvectors: Grasping the concepts of eigenvalues and eigenvectors, which are crucial for dimensionality reduction and principal component analysis (PCA).
- Singular Value Decomposition (SVD): Knowing how to decompose matrices using SVD, a powerful technique for data compression and noise reduction.
2.1.2. Linear Algebra in Machine Learning
Linear algebra is used extensively in machine learning for:
- Data Representation: Representing data points as vectors and datasets as matrices.
- Dimensionality Reduction: Reducing the number of features in a dataset using PCA and SVD.
- Recommendation Systems: Building recommendation systems using matrix factorization techniques.
- Image Processing: Manipulating images using linear transformations.
2.2. Calculus
Calculus is the math of change. It provides tools for understanding how functions behave, finding their extrema, and optimizing model parameters.
2.2.1. Key Concepts in Calculus
- Derivatives: Understanding the concept of derivatives and how to compute them.
- Gradients: Grasping the concept of gradients and their role in optimization.
- Chain Rule: Knowing how to apply the chain rule to compute derivatives of composite functions.
- Integration: Understanding the concept of integration and its applications.
2.2.2. Calculus in Machine Learning
Calculus is used extensively in machine learning for:
- Optimization: Optimizing model parameters using gradient descent and other optimization algorithms.
- Neural Networks: Training neural networks using backpropagation, which relies on calculus.
- Loss Functions: Defining and minimizing loss functions to improve model performance.
- Regularization: Adding regularization terms to loss functions to prevent overfitting.
2.3. Probability and Statistics
Probability and statistics provide the tools to model uncertainty, analyze data distributions, and evaluate model performance.
2.3.1. Key Concepts in Probability and Statistics
- Probability Distributions: Understanding common probability distributions like normal, binomial, and Poisson.
- Hypothesis Testing: Knowing how to perform hypothesis tests to validate statistical claims.
- Confidence Intervals: Grasping the concept of confidence intervals and how to compute them.
- Regression Analysis: Understanding how to perform regression analysis to model relationships between variables.
2.3.2. Probability and Statistics in Machine Learning
Probability and statistics are used extensively in machine learning for:
- Data Analysis: Analyzing data distributions and identifying patterns.
- Model Evaluation: Evaluating model performance using metrics like accuracy, precision, and recall.
- Bayesian Methods: Implementing Bayesian machine learning algorithms.
- Statistical Inference: Drawing conclusions about populations based on sample data.
3. Learning Math for Machine Learning: A Step-by-Step Guide
Learning math for machine learning can seem daunting, but with a structured approach, you can build a solid foundation and gain the skills you need to succeed.
3.1. Step 1: Assess Your Current Math Skills
Before diving into new material, take stock of your current math skills. Identify areas where you feel confident and areas where you need to improve. This assessment will help you tailor your learning plan and focus on the most relevant topics.
3.2. Step 2: Choose the Right Resources
Numerous resources are available for learning math for machine learning, including online courses, textbooks, and tutorials. Select resources that match your learning style and skill level.
3.2.1. Online Courses
- Coursera: Offers courses on linear algebra, calculus, and probability and statistics from top universities.
- edX: Provides similar courses with a focus on hands-on learning.
- Khan Academy: Offers free math tutorials covering a wide range of topics.
- Udacity: Provides in-depth courses on machine learning with a strong emphasis on math.
3.2.2. Textbooks
- “Linear Algebra and Its Applications” by Gilbert Strang: A classic textbook on linear algebra.
- “Calculus” by James Stewart: A comprehensive textbook on calculus.
- “Probability and Statistics for Engineers and Scientists” by Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers, and Keying Ye: A popular textbook on probability and statistics.
3.2.3. Online Tutorials
- 3Blue1Brown: Offers visually engaging math tutorials on linear algebra and calculus.
- StatQuest: Provides clear and concise explanations of statistical concepts.
3.3. Step 3: Create a Study Plan
Develop a structured study plan that outlines the topics you want to cover, the resources you’ll use, and the time you’ll allocate to each topic. Break down your learning into manageable chunks and set realistic goals.
Example Study Plan (12 Weeks)
| Week | Topic | Resources | Hours/Week |
|---|---|---|---|
| 1-3 | Linear Algebra Fundamentals | Gilbert Strang’s “Linear Algebra and Its Applications,” 3Blue1Brown | 10 |
| 4-6 | Calculus Fundamentals | James Stewart’s “Calculus,” Khan Academy | 10 |
| 7-9 | Probability & Statistics | Walpole et al.’s “Probability and Statistics,” StatQuest | 10 |
| 10-12 | Math for Machine Learning | Coursera’s “Mathematics for Machine Learning,” Practical Exercises | 10 |
3.4. Step 4: Practice Regularly
Math is a skill that requires practice. Work through examples, solve problems, and apply your knowledge to real-world datasets. The more you practice, the more comfortable you’ll become with the material.
3.5. Step 5: Seek Help When Needed
Don’t be afraid to ask for help when you’re struggling. Join online forums, attend study groups, or seek guidance from mentors or instructors. Collaboration can accelerate your learning and help you overcome challenges.
3.6. Step 6: Apply Your Knowledge
Once you’ve gained a solid understanding of the fundamental math concepts, start applying your knowledge to machine-learning problems. Work on projects, participate in competitions, and build models using real-world data.
4. The Role of Math in Different Machine Learning Algorithms
Let’s explore how math is used in various machine learning algorithms.
4.1. Linear Regression
Linear regression is a simple yet powerful algorithm for modeling the relationship between a dependent variable and one or more independent variables.
4.1.1. Math Behind Linear Regression
- Linear Algebra: Used to represent the data and model parameters.
- Calculus: Used to optimize the model parameters by minimizing the sum of squared errors.
- Statistics: Used to evaluate the model’s performance and assess the significance of the coefficients.
4.1.2. Example
Given a dataset of house prices and their corresponding sizes, linear regression can be used to model the relationship between house size and price. The model parameters (slope and intercept) are optimized using calculus to minimize the difference between the predicted prices and the actual prices.
4.2. Logistic Regression
Logistic regression is a classification algorithm used to predict the probability of a binary outcome (e.g., spam or not spam).
4.2.1. Math Behind Logistic Regression
- Calculus: Used to optimize the model parameters by maximizing the likelihood function.
- Statistics: Used to evaluate the model’s performance and assess the significance of the coefficients.
- Linear Algebra: Essential for handling the vector of coefficients and input features.
4.2.2. Example
Given a dataset of emails and their corresponding features (e.g., word frequencies), logistic regression can be used to classify emails as spam or not spam. The model parameters are optimized using calculus to maximize the likelihood of correctly classifying the emails.
4.3. Support Vector Machines (SVM)
Support Vector Machines (SVMs) are powerful algorithms for classification and regression tasks.
4.3.1. Math Behind SVM
- Linear Algebra: Used to represent the data and model parameters.
- Calculus: Used to optimize the model parameters by maximizing the margin between the classes.
- Optimization Theory: Applied to solve the quadratic programming problem that arises in SVM training.
4.3.2. Example
Given a dataset of images and their corresponding labels (e.g., cat or dog), an SVM can be used to classify the images. The model parameters are optimized to maximize the margin between the cat and dog classes.
4.4. Neural Networks
Neural networks are complex algorithms inspired by the structure of the human brain. They are used for a wide range of tasks, including image recognition, natural language processing, and speech recognition.
4.4.1. Math Behind Neural Networks
- Calculus: Used to train the network using backpropagation, which involves computing gradients of the loss function with respect to the network parameters.
- Linear Algebra: Used to perform matrix operations and represent the network layers.
- Probability: Used to model the uncertainty in the network’s predictions.
4.4.2. Example
Given a dataset of images and their corresponding labels (e.g., handwritten digits), a neural network can be trained to recognize the digits. The network parameters are optimized using backpropagation to minimize the difference between the predicted labels and the actual labels.
5. Overcoming Math Anxiety: Tips and Strategies
Math anxiety is a common obstacle for many learners. Here are some tips and strategies to overcome it.
5.1. Start with the Basics
If you’re feeling overwhelmed, start with the basics. Review fundamental concepts and build a solid foundation before moving on to more advanced topics.
5.2. Break Down Complex Problems
Break down complex problems into smaller, more manageable steps. Solve each step individually and then combine the solutions to solve the overall problem.
5.3. Use Visual Aids
Use visual aids such as diagrams, graphs, and charts to help you understand math concepts. Visual aids can make abstract ideas more concrete and easier to grasp.
5.4. Practice Regularly
Practice regularly to build your confidence and skills. The more you practice, the more comfortable you’ll become with the material.
5.5. Seek Support
Seek support from friends, family, or mentors. Talking to someone about your struggles can help you overcome your anxiety and gain new perspectives.
5.6. Celebrate Small Wins
Celebrate your small wins along the way. Recognizing your progress can boost your confidence and motivate you to keep learning.
6. Advanced Math Topics for Machine Learning
Once you have a solid foundation in linear algebra, calculus, and probability and statistics, you can explore more advanced math topics.
6.1. Optimization Theory
Optimization theory deals with finding the best solution to a problem. It is used extensively in machine learning to optimize model parameters and improve performance.
6.1.1. Key Concepts in Optimization Theory
- Convex Optimization: Understanding the properties of convex functions and their role in optimization.
- Gradient Descent: Knowing how to implement gradient descent and its variants.
- Lagrange Multipliers: Grasping the concept of Lagrange multipliers and their applications.
6.2. Information Theory
Information theory deals with the quantification, storage, and communication of information. It is used in machine learning for feature selection, model evaluation, and data compression.
6.2.1. Key Concepts in Information Theory
- Entropy: Understanding the concept of entropy and its role in measuring uncertainty.
- Mutual Information: Knowing how to compute mutual information between variables.
- Kullback-Leibler Divergence: Grasping the concept of Kullback-Leibler divergence and its applications.
6.3. Functional Analysis
Functional analysis deals with the study of vector spaces and linear operators. It is used in machine learning for kernel methods, regularization, and model selection.
6.3.1. Key Concepts in Functional Analysis
- Hilbert Spaces: Understanding the properties of Hilbert spaces and their role in machine learning.
- Reproducing Kernel Hilbert Spaces (RKHS): Knowing how to construct RKHS and their applications.
- Mercer’s Theorem: Grasping the concept of Mercer’s theorem and its implications.
7. Practical Applications of Math in Machine Learning
Let’s look at some practical applications of math in machine learning.
7.1. Image Recognition
Math is used extensively in image recognition for:
- Image Processing: Applying linear transformations to images.
- Feature Extraction: Extracting features from images using convolutional neural networks.
- Classification: Classifying images using support vector machines or neural networks.
7.2. Natural Language Processing (NLP)
Math is used extensively in natural language processing for:
- Text Processing: Tokenizing and stemming text.
- Feature Extraction: Extracting features from text using bag-of-words or TF-IDF.
- Classification: Classifying text using logistic regression or support vector machines.
7.3. Recommendation Systems
Math is used extensively in recommendation systems for:
- Matrix Factorization: Decomposing user-item matrices using SVD.
- Collaborative Filtering: Recommending items based on the preferences of similar users.
- Content-Based Filtering: Recommending items based on their similarity to items the user has liked in the past.
8. Resources for Continued Learning
To continue your learning journey, here are some valuable resources.
8.1. Online Communities
- Stack Overflow: A question-and-answer website for programmers and data scientists.
- Reddit: A social media platform with subreddits dedicated to machine learning and data science.
- Kaggle: A platform for data science competitions and collaboration.
8.2. Blogs and Websites
- Towards Data Science: A Medium publication with articles on machine learning and data science.
- Machine Learning Mastery: A website with tutorials and resources on machine learning.
- Analytics Vidhya: A website with articles and courses on data science and analytics.
8.3. Books
- “The Elements of Statistical Learning” by Trevor Hastie, Robert Tibshirani, and Jerome Friedman: A comprehensive textbook on statistical learning.
- “Pattern Recognition and Machine Learning” by Christopher Bishop: A popular textbook on machine learning.
- “Deep Learning” by Ian Goodfellow, Yoshua Bengio, and Aaron Courville: A comprehensive textbook on deep learning.
9. Adapting to New Trends in Machine Learning
The field of machine learning is constantly evolving. To stay current, it’s important to adapt to new trends and technologies.
9.1. Staying Updated with Research
Keep up with the latest research by reading academic papers and attending conferences. This will help you stay informed about new algorithms, techniques, and applications of machine learning.
9.2. Exploring New Tools and Technologies
Experiment with new tools and technologies, such as cloud computing platforms, deep learning frameworks, and data visualization libraries. This will help you expand your skillset and stay competitive in the job market.
9.3. Continuous Learning
Commit to continuous learning and professional development. Take online courses, attend workshops, and participate in industry events to expand your knowledge and skills.
10. Frequently Asked Questions (FAQs) About Math in Machine Learning
Let’s address some common questions about the role of math in machine learning.
10.1. How much math do I really need for machine learning?
You need a solid foundation in linear algebra, calculus, and probability and statistics. The more you understand these concepts, the better equipped you’ll be to tackle complex machine learning problems.
10.2. Can I learn machine learning without math?
While it’s possible to use machine learning libraries without a deep understanding of math, you’ll be limited in your ability to customize algorithms, diagnose problems, and innovate.
10.3. What if I’m not good at math?
Don’t let a lack of confidence in math hold you back. Start with the basics, practice regularly, and seek help when needed. With persistence and effort, you can improve your math skills and succeed in machine learning.
10.4. How long does it take to learn the math needed for machine learning?
The time it takes to learn the math needed for machine learning depends on your background, learning style, and the depth of knowledge you desire. A dedicated study plan of 10-15 hours per week for 6-12 months can provide a solid foundation.
10.5. What are the best resources for learning math for machine learning?
Excellent resources include online courses (Coursera, edX, Khan Academy), textbooks (“Linear Algebra and Its Applications” by Gilbert Strang, “Calculus” by James Stewart), and online tutorials (3Blue1Brown, StatQuest).
10.6. Do I need a degree in math to work in machine learning?
No, a degree in math is not required, but a strong understanding of math is essential. Many successful machine learning practitioners come from diverse backgrounds, including computer science, engineering, and physics.
10.7. How can I apply math to real-world machine learning problems?
Work on projects, participate in competitions, and build models using real-world data. This will help you apply your knowledge and gain practical experience.
10.8. What advanced math topics should I learn for machine learning?
Advanced math topics include optimization theory, information theory, and functional analysis. These topics will help you tackle more complex machine learning problems and develop new algorithms.
10.9. How can I stay updated with the latest math developments in machine learning?
Read academic papers, attend conferences, and participate in online communities. This will help you stay informed about new algorithms, techniques, and applications of math in machine learning.
10.10. Where can I find a supportive community to discuss math and machine learning?
Join online forums, attend study groups, and seek guidance from mentors or instructors. Collaboration can accelerate your learning and help you overcome challenges.
Math is undeniably crucial for machine learning. By mastering the essential concepts and continuously learning, you can unlock the full potential of machine learning and build innovative solutions to real-world problems.
Math is a Cornerstone of ML Learning Path
The path to mastering machine learning involves a commitment to understanding and applying mathematical concepts. This journey, while challenging, is incredibly rewarding, opening doors to innovative problem-solving and cutting-edge research.
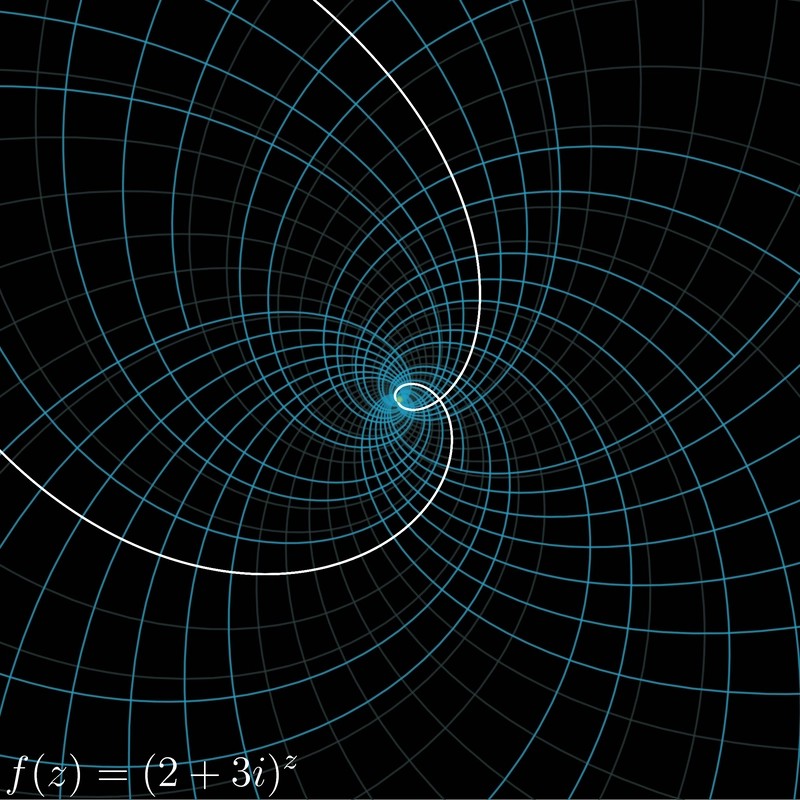
Visualizing Math for Enhanced Understanding
3Blue1Brown’s approach to visualizing linear algebra and calculus provides an intuitive grasp of complex mathematical principles, making them accessible and easier to apply in machine learning contexts. This visual understanding is invaluable for anyone looking to deepen their expertise in the field.
At LEARNS.EDU.VN, we understand the challenges and rewards of learning math for machine learning. We provide comprehensive resources, step-by-step guides, and expert support to help you build a solid foundation and achieve your goals.
Ready to take your machine learning skills to the next level? Visit learns.edu.vn today and explore our courses and resources. Whether you’re a beginner or an experienced practitioner, we have something for you. Contact us at 123 Education Way, Learnville, CA 90210, United States, or WhatsApp: +1 555-555-1212. Let’s embark on this exciting journey together!
