At LEARNS.EDU.VN, we understand that understanding how loss is calculated in machine learning is fundamental to building effective models. This comprehensive guide provides a deep dive into loss functions, also known as cost functions or error functions, and their crucial role in optimizing machine learning algorithms. We’ll explore various types of loss metrics, including those used in regression and classification tasks, and how they drive the learning process.
1. Understanding Loss Functions in Machine Learning
Loss functions are at the heart of machine learning, serving as the compass that guides algorithms toward optimal performance. They quantify the discrepancy between a model’s predictions and the actual, desired outcomes. In essence, a loss function measures how “wrong” a model is on a given dataset.
Think of it this way: imagine you’re teaching a dog to fetch. Each time the dog brings back the wrong object, you give a signal – a verbal correction or a slight tug on the leash. The loss function is like that signal, providing feedback to the algorithm about its mistakes. The goal of the algorithm is to minimize this “loss” over time, learning to make more accurate predictions. This optimization process is crucial for achieving high accuracy and reliability in machine learning models. Loss functions drive this optimization, allowing algorithms to learn from errors and improve their predictive capabilities. At LEARNS.EDU.VN, we empower you with a deep understanding of these concepts, helping you build robust and reliable machine learning models.
2. The Role of Loss Functions in Deep Learning
Deep learning models, with their intricate neural networks, rely heavily on loss functions to learn complex patterns in data. The loss function guides the adjustment of weights and biases within the network, iteratively refining the model’s ability to map inputs to desired outputs. Without a well-defined loss function, the learning process would be aimless, and the model would fail to converge on a useful solution.
In deep learning, the choice of loss function is a critical design decision that directly impacts the model’s performance. Whether it’s regression, classification, or a more specialized task, selecting the right loss function ensures that the model learns the appropriate features and relationships within the data. It also helps to prevent issues like overfitting or underfitting. This underscores the importance of carefully considering the nature of the problem and the characteristics of the data when selecting or designing a loss function.
3. Cost Functions in Machine Learning: An Overview
While the terms “loss function” and “cost function” are often used interchangeably, there’s a subtle distinction. A loss function typically refers to the error for a single data point, while a cost function represents the average loss over the entire training dataset. In other words, the cost function is the aggregate measure of how well the model is performing across all the data it has seen.
Cost functions provide a global view of the model’s performance and are used to guide the optimization process. Algorithms like gradient descent use the cost function to determine the direction in which to adjust the model’s parameters to reduce the overall error. By minimizing the cost function, the model learns to generalize well to unseen data, making accurate predictions on new inputs. Understanding the difference between loss and cost functions is important for comprehending how machine learning algorithms learn and optimize their performance.
4. Key Differences: Loss Functions vs. Cost Functions
To solidify the understanding of these two terms, let’s highlight the key differences in a clear table:
| Feature | Loss Function | Cost Function |
|---|---|---|
| Scope | Error for a single data point | Average error over the entire training dataset |
| Purpose | Measure error for individual predictions | Guide optimization and evaluate overall performance |
| Calculation | Direct calculation based on prediction & target | Aggregate of loss function values |
| Example | Squared error for one instance | Mean Squared Error (MSE) for all instances |
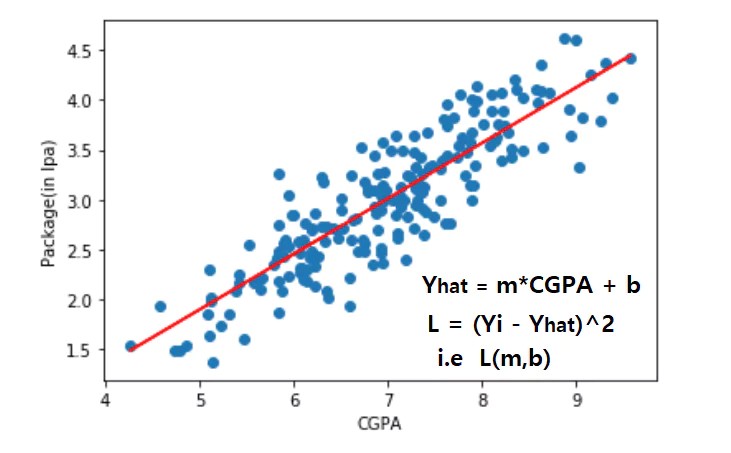
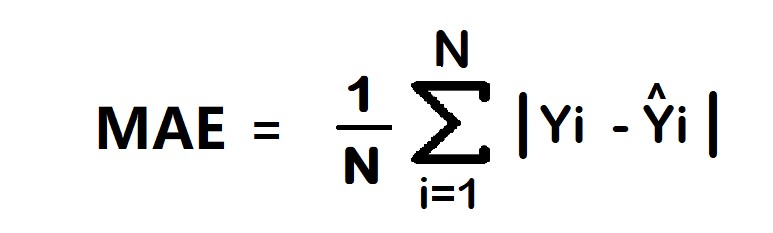
5. The Pivotal Role of Loss Functions in Machine Learning Algorithms
Loss functions are not merely passive observers; they actively shape the learning process in machine learning algorithms. They act as the objective function that algorithms strive to minimize. By quantifying the error between predictions and actual values, loss functions provide a clear signal to the algorithm about how to adjust its parameters to improve accuracy.
Consider the analogy of a sculptor shaping a statue. The loss function is like the sculptor’s eye, constantly evaluating the form and guiding the movements of the chisel. Each adjustment is made with the goal of minimizing imperfections and bringing the statue closer to the desired form. Similarly, machine learning algorithms use the loss function to iteratively refine their models, adjusting parameters to reduce the error and improve predictive performance. This iterative optimization process is at the core of machine learning, and the loss function plays a vital role in guiding the algorithm towards the best possible solution.
6. Regression Loss Functions: Predicting Continuous Values
In regression tasks, where the goal is to predict continuous values, several loss functions are commonly used. Let’s explore some of the most popular options:
6.1. Mean Squared Error (MSE)
MSE, also known as L2 loss, is one of the most widely used regression loss functions. It calculates the average of the squared differences between the predicted and actual values.
Formula:
MSE = (1/n) * Σ(yi – ŷi)^2
Where:
- n = number of data points
- yi = actual value
- ŷi = predicted value
Advantages:
- Easy to understand and implement
- Differentiable, which is important for gradient-based optimization algorithms
- Penalizes large errors more heavily than smaller errors
Disadvantages:
- Sensitive to outliers, as the squared error magnifies the impact of large deviations
- The error unit is in squared form, which might not be intuitively interpretable
6.2. Mean Absolute Error (MAE)
MAE, also known as L1 loss, calculates the average of the absolute differences between the predicted and actual values.
Formula:
MAE = (1/n) * Σ|yi – ŷi|
Where:
- n = number of data points
- yi = actual value
- ŷi = predicted value
Advantages:
- Intuitive and easy to understand
- Less sensitive to outliers compared to MSE
- The error unit matches the output column
Disadvantages:
- Not differentiable at zero, which can cause issues for gradient-based optimization
- Doesn’t penalize large errors as heavily as MSE
6.3. Huber Loss
Huber loss is a robust loss function that combines the best aspects of MSE and MAE. It is less sensitive to outliers than MSE while still being differentiable.
Formula:
Huber Loss = {
0.5 (yi – ŷi)^2 for |yi – ŷi| <= δ
δ |yi – ŷi| – 0.5 * δ^2 for |yi – ŷi| > δ
}
Where:
- n = number of data points
- yi = actual value
- ŷi = predicted value
- δ = a threshold parameter that defines the point where the loss transitions from quadratic to linear
Advantages:
- Robust to outliers
- Balances MAE and MSE
Disadvantages:
- Requires tuning the hyperparameter δ, which can increase training complexity
Table: Comparison of Regression Loss Functions
| Loss Function | Formula | Advantages | Disadvantages |
|---|---|---|---|
| MSE | (1/n) * Σ(yi – ŷi)^2 | Easy to understand, differentiable, penalizes large errors heavily | Sensitive to outliers, error unit in squared form |
| MAE | (1/n) * Σ | yi – ŷi | |
| Huber Loss | Piecewise function based on threshold δ | Robust to outliers, balances MAE and MSE | Requires tuning hyperparameter δ, increased training complexity |
7. Classification Loss Functions: Predicting Categories
In classification tasks, where the goal is to predict the category or class to which a data point belongs, different loss functions are used. Let’s examine some of the most common choices:
7.1. Binary Cross-Entropy
Binary cross-entropy is used in binary classification problems, where there are only two possible classes (e.g., yes/no, spam/not spam).
Formula:
Binary Cross-Entropy = – (yi log(ŷi) + (1 – yi) log(1 – ŷi))
Where:
- yi = actual value (0 or 1)
- ŷi = predicted probability (between 0 and 1)
Advantages:
- Differentiable
- Well-suited for binary classification problems
Disadvantages:
- Can suffer from multiple local minima
- Not as intuitive as other loss functions
7.2. Categorical Cross-Entropy
Categorical cross-entropy is used in multi-class classification problems, where there are more than two possible classes (e.g., classifying images into different categories).
Formula:
Categorical Cross-Entropy = – Σ (yi,c * log(ŷi,c))
Where:
- yi,c = actual value (0 or 1) for class c
- ŷi,c = predicted probability for class c
- The sum is taken over all classes
Advantages:
- Well-suited for multi-class classification problems
- Differentiable
Disadvantages:
- Requires one-hot encoding of the target variable
- Can be computationally expensive for a large number of classes
7.3. Sparse Categorical Cross-Entropy
Sparse categorical cross-entropy is similar to categorical cross-entropy but is used when the target variable is represented as integers rather than one-hot encoded vectors.
Advantages:
- More memory-efficient than categorical cross-entropy when dealing with a large number of classes
- Faster than categorical cross-entropy
Disadvantages:
- Requires the target variable to be represented as integers
- Slightly less flexible than categorical cross-entropy
Table: Comparison of Classification Loss Functions
| Loss Function | Use Case | Advantages | Disadvantages |
|---|---|---|---|
| Binary Cross-Entropy | Binary classification | Differentiable, well-suited for binary problems | Can suffer from multiple local minima, not as intuitive |
| Categorical Cross-Entropy | Multi-class classification | Well-suited for multi-class problems, differentiable | Requires one-hot encoding, computationally expensive for many classes |
| Sparse Categorical CE | Multi-class classification (integer labels) | Memory-efficient, faster than categorical CE | Requires integer labels, slightly less flexible |
8. When to Use Categorical Cross-Entropy and Sparse Categorical Cross-Entropy?
Choosing between categorical and sparse categorical cross-entropy depends on how your target variable is encoded:
- Categorical Cross-Entropy: Use this when your target variable is one-hot encoded. For example, if you have three classes, your labels might look like [1, 0, 0], [0, 1, 0], and [0, 0, 1].
- Sparse Categorical Cross-Entropy: Use this when your target variable is represented as integers. For example, if you have three classes, your labels might look like 0, 1, and 2.
Using sparse categorical cross-entropy can be more memory-efficient, especially when dealing with a large number of classes.
9. Optimizing Loss Functions: Gradient Descent and Beyond
Once a loss function is defined, the next step is to minimize it using optimization algorithms. Gradient descent is one of the most commonly used algorithms for this purpose.
Gradient descent works by iteratively adjusting the model’s parameters in the direction of the steepest descent of the loss function. The gradient of the loss function indicates the direction in which the loss is increasing, so by moving in the opposite direction, the algorithm can gradually reduce the loss and improve the model’s performance.
However, gradient descent can be slow and may get stuck in local minima. To overcome these limitations, more advanced optimization algorithms have been developed, such as:
- Stochastic Gradient Descent (SGD): Updates the parameters using the gradient of the loss function for a single data point or a small batch of data points.
- Adam: An adaptive optimization algorithm that combines the benefits of both AdaGrad and RMSProp.
- RMSProp: An adaptive learning rate optimization algorithm that adjusts the learning rate for each parameter based on the magnitude of its recent gradients.
10. The Impact of Data Distribution on Loss Function Selection
The distribution of your data can significantly impact the performance of different loss functions. For example, if your data contains outliers, MSE may be overly sensitive, while MAE or Huber loss might be more robust choices.
Similarly, if your data is imbalanced (i.e., one class has significantly more samples than the other), you may need to use a weighted loss function or other techniques to address the imbalance. Understanding the characteristics of your data is crucial for selecting the most appropriate loss function for your machine-learning task. At LEARNS.EDU.VN, we offer resources and guidance to help you analyze your data and make informed decisions about loss function selection.
11. Real-World Applications of Different Loss Functions
Let’s explore some real-world examples of how different loss functions are used in various applications:
Scenario 1: Predicting House Prices (Regression)
- Problem: Predict the price of a house based on features like size, location, and number of bedrooms.
- Loss Function: MSE is often used in this scenario, as it provides a good balance between accuracy and sensitivity to errors. However, if there are many outliers (e.g., extremely expensive or cheap houses), Huber loss might be a better choice.
Scenario 2: Image Classification (Multi-Class Classification)
- Problem: Classify images of animals into different categories (e.g., dog, cat, bird).
- Loss Function: Categorical cross-entropy is the standard choice for this type of problem, as it is well-suited for multi-class classification.
Scenario 3: Spam Detection (Binary Classification)
- Problem: Classify emails as either spam or not spam.
- Loss Function: Binary cross-entropy is the natural choice for this binary classification task.
Scenario 4: Object Detection (Regression and Classification)
- Problem: Identify and locate objects within an image.
- Loss Function: Object detection often involves a combination of regression (to predict the bounding box coordinates) and classification (to predict the object class). Therefore, it may use a combination of loss functions, such as MSE for the bounding box regression and categorical cross-entropy for the class prediction.
12. Custom Loss Functions: Tailoring to Specific Needs
While standard loss functions are often sufficient, there are cases where you may need to define a custom loss function to meet the specific needs of your application. This is particularly true when dealing with complex or unconventional problems.
When defining a custom loss function, it’s important to ensure that it is:
- Differentiable: For use with gradient-based optimization algorithms
- Meaningful: Reflects the true cost of making errors in your specific application
- Well-Behaved: Avoids issues like vanishing gradients or exploding gradients
Creating a custom loss function requires a deep understanding of your problem and the mathematical principles underlying machine learning.
13. Addressing Common Challenges in Loss Function Optimization
Optimizing loss functions can be challenging, and several common issues can arise:
- Local Minima: Gradient descent may get stuck in a local minimum, which is a point where the loss is lower than its neighbors but not the global minimum.
- Vanishing Gradients: In deep neural networks, gradients can become very small as they are backpropagated through the layers, making it difficult for the model to learn.
- Exploding Gradients: Conversely, gradients can become very large, causing the model to become unstable and diverge.
Techniques for addressing these challenges include:
- Using different optimization algorithms: Adam, RMSProp, and other adaptive algorithms can help to overcome the limitations of standard gradient descent.
- Using regularization techniques: L1 and L2 regularization can help to prevent overfitting and improve the generalization performance of the model.
- Using batch normalization: Batch normalization can help to stabilize the training process and prevent vanishing or exploding gradients.
- Careful initialization of weights: Initializing the weights of the neural network properly can help to avoid getting stuck in local minima or experiencing vanishing gradients.
14. Loss Functions and Model Evaluation Metrics
It’s important to distinguish between loss functions and model evaluation metrics. While loss functions are used to guide the training process, evaluation metrics are used to assess the model’s performance on a separate validation or test dataset.
Common evaluation metrics for regression tasks include:
- R-squared: Measures the proportion of variance in the dependent variable that is predictable from the independent variables.
- Root Mean Squared Error (RMSE): The square root of the MSE, providing an error measure in the same units as the target variable.
Common evaluation metrics for classification tasks include:
- Accuracy: The proportion of correctly classified instances.
- Precision: The proportion of true positives among the instances predicted as positive.
- Recall: The proportion of true positives that were correctly identified.
- F1-Score: The harmonic mean of precision and recall, providing a balanced measure of performance.
- AUC-ROC: The area under the receiver operating characteristic curve, measuring the model’s ability to discriminate between classes.
While a low loss value is desirable, it doesn’t necessarily guarantee good performance on the evaluation metrics. It’s important to monitor both the loss function and the evaluation metrics to ensure that the model is generalizing well to unseen data.
15. The Future of Loss Functions: Trends and Innovations
The field of loss functions is constantly evolving, with new research and innovations emerging all the time. Some of the current trends include:
- Adversarial Loss Functions: Used in generative adversarial networks (GANs) to train generators and discriminators.
- Contrastive Loss Functions: Used in self-supervised learning to learn representations that capture the similarity between data points.
- Focal Loss: Designed to address the issue of class imbalance in object detection.
- Loss functions incorporating domain knowledge: These loss functions are designed to incorporate specific constraints or knowledge about the problem domain.
As machine learning continues to advance, we can expect to see even more sophisticated and specialized loss functions being developed to address the challenges of new applications and datasets.
16. Resources for Further Learning at LEARNS.EDU.VN
At LEARNS.EDU.VN, we are committed to providing you with the knowledge and resources you need to master the concepts of machine learning and loss functions. We offer a range of courses, tutorials, and articles that delve deeper into these topics.
Specifically, we recommend the following resources:
- Machine Learning Fundamentals Course: A comprehensive introduction to the core concepts of machine learning, including loss functions, optimization algorithms, and model evaluation.
- Deep Learning Specialization: A series of courses that cover the fundamentals of deep learning, including neural networks, convolutional neural networks, and recurrent neural networks.
- Advanced Loss Functions Tutorial: A hands-on tutorial that explores the implementation and use of custom loss functions.
- Blog Articles on Machine Learning Best Practices: Stay up-to-date with the latest trends and techniques in machine learning, including best practices for selecting and optimizing loss functions.
17. FAQs about Loss Calculation in Machine Learning
Q1: What is a loss function?
A: A loss function quantifies the difference between predicted and actual values in machine learning. It helps algorithms learn by measuring errors and guiding parameter adjustments.
Q2: Is the loss function always between 0 and 1?
A: No, the range of a loss function varies depending on the specific function used. For example, Mean Squared Error can range from 0 to infinity, while Binary Cross-Entropy is typically between 0 and infinity as well but bounded depending on the output probabilities.
Q3: What is the loss function in macroeconomics?
A: In macroeconomics, a loss function counts deviations from production and inflation targets, where both negative and positive deviations are considered losses.
Q4: What are the benefits of using a loss function?
A: Loss functions are crucial for assessing model performance, guiding models during training, and determining the optimal parameter set to minimize errors.
Q5: How do loss functions help in model optimization?
A: Loss functions provide a measure of error that optimization algorithms, like gradient descent, use to adjust model parameters iteratively, leading to better predictions.
Q6: What’s the difference between MSE and MAE?
A: MSE (Mean Squared Error) calculates the average squared difference between predicted and actual values, penalizing larger errors more. MAE (Mean Absolute Error) calculates the average absolute difference, making it less sensitive to outliers.
Q7: When should I use categorical cross-entropy over binary cross-entropy?
A: Use categorical cross-entropy for multi-class classification problems (more than two classes) and binary cross-entropy for binary classification problems (two classes).
Q8: Why is data distribution important when choosing a loss function?
A: Data distribution affects the performance of different loss functions. For example, outliers can heavily influence MSE, making MAE or Huber loss better choices.
Q9: Can I create my own custom loss function?
A: Yes, you can define a custom loss function to meet specific application needs, ensuring it is differentiable, meaningful, and well-behaved.
Q10: What are some common challenges in loss function optimization?
A: Common challenges include local minima, vanishing gradients, and exploding gradients. These can be addressed using advanced optimization algorithms, regularization techniques, and batch normalization.
18. Conclusion: Mastering Loss Calculation for Machine Learning Success
Understanding how loss is calculated in machine learning is essential for building effective and reliable models. By carefully selecting and optimizing loss functions, you can guide your algorithms towards optimal performance and achieve your desired outcomes.
At LEARNS.EDU.VN, we are dedicated to empowering you with the knowledge and skills you need to succeed in the field of machine learning. Whether you’re a beginner or an experienced practitioner, we have the resources and expertise to help you master the concepts of loss functions and build cutting-edge machine learning solutions.
Ready to take your machine learning skills to the next level? Visit LEARNS.EDU.VN today to explore our comprehensive courses and resources. Learn from expert instructors, gain hands-on experience, and unlock your full potential in the exciting world of machine learning.
Contact Us:
Address: 123 Education Way, Learnville, CA 90210, United States
WhatsApp: +1 555-555-1212
Website: learns.edu.vn
We are excited to partner with you on your journey to machine learning mastery!