Statistics are fundamental to machine learning. Discover its applications, benefits, and more with insights from LEARNS.EDU.VN, guiding you to mastery. Unlock your potential today.
Machine learning thrives on statistics, shaping its core and foundational rules. Without proper statistical integration, machine learning wouldn’t exist. Explore how statistics are used in machine learning, statistical learning, statistical modeling and statistical analysis to elevate your expertise, enhance model performance, and ensure objective evaluation.
1. Introduction to the Role of Statistics in Machine Learning
Machine learning (ML) is revolutionizing numerous fields, with healthcare at the forefront, thanks to rapid advancements in computing technology and the exponential growth of available data. This data explosion necessitates sophisticated methods to extract meaningful insights, where machine learning algorithms play a crucial role.
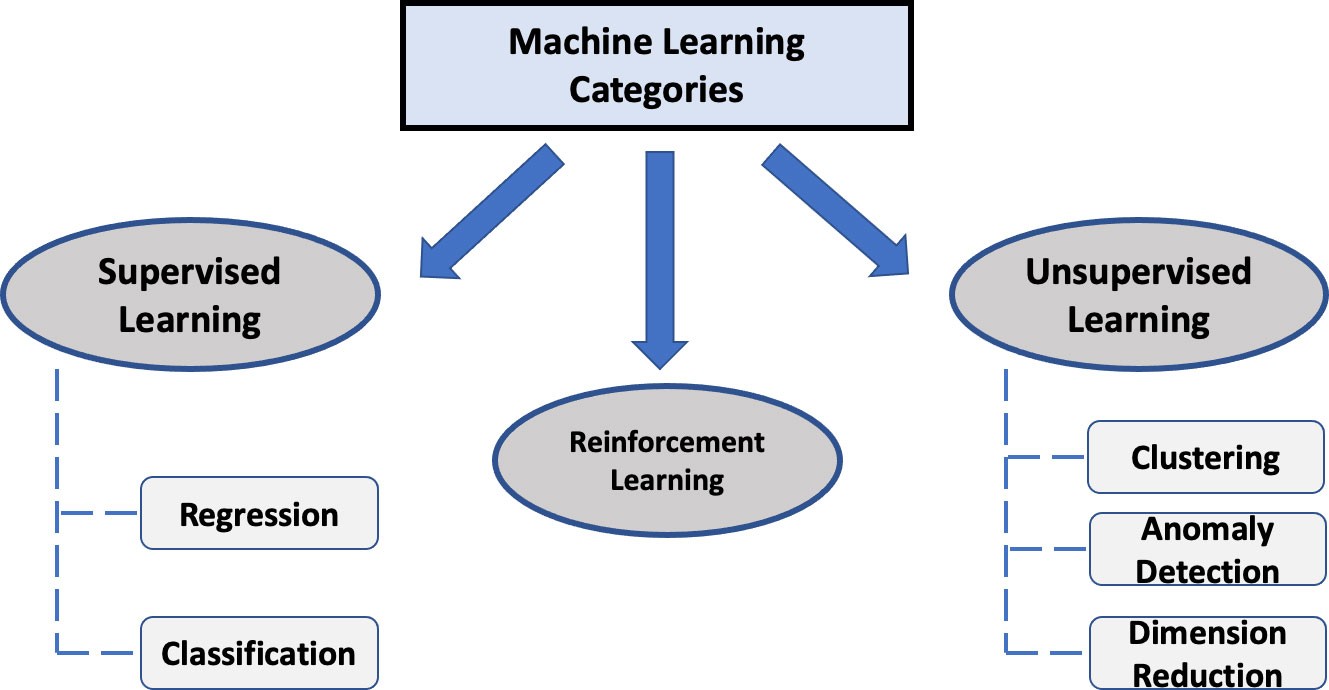
ML, a subset of artificial intelligence (AI), relies heavily on statistics and computer science. It identifies patterns and relationships in data through computationally enhanced algorithms. ML algorithms are broadly categorized into:
- Supervised learning
- Unsupervised learning
- Reinforcement learning
Figure 1: Common categories of machine learning algorithms, showcasing the diversity and applications within each type.
1.1 Supervised Learning
Supervised learning uses datasets with labeled outputs (target variables). A supervised ML model is developed to predict these outputs using the remaining variables (features) by uncovering or approximating relationships between them. In healthcare, supervised ML is used for:
- Disease diagnosis (e.g., cancer detection)
- Predicting treatment responses
- Forecasting patient outcomes
1.2 Unsupervised Learning
Unsupervised learning deals with unlabeled data, aiming to identify subgroups or clusters with similar patterns without human intervention. This approach, often called clustering analysis, uses methods like:
- K-means clustering
- Hierarchical clustering
- Principal component analysis (PCA)
- Anomaly detection
These methods can cluster data features or subjects. In healthcare, unsupervised learning can redefine diseases by clustering patients, supporting precision medicine initiatives. For deeper insights into unsupervised methods like PCA, learns.edu.vn offers comprehensive resources.
1.3 Reinforcement Learning
Reinforcement learning (RL) uses a sequential decision-making process, sharing features with both supervised and unsupervised learning. It teaches machines through trial and error, adapting actions based on past experiences to maximize rewards. Although not yet common in healthcare, RL is emerging in dynamic treatment regimens, aiming to identify optimal intervention sequences based on patient characteristics and medical histories.
This article focuses on the statistical concepts within supervised ML (regression and classification), their interdependencies, and limitations, providing a comprehensive overview of how statistics are used in machine learning.
2. Supervised Machine Learning: An Overview
Supervised ML models are primarily divided into regression and classification. Regression deals with continuous numerical outputs (e.g., blood pressure), while classification handles categorical outputs (e.g., cancer vs. normal tissue). In ML, “regression” differs slightly from statistics, where it can also refer to models for categorical outputs like logistic regression.
2.1 Core Concept
The primary goal of supervised learning is to model the statistical relationship between feature variables (independent variables) and the output (target or dependent variables). A supervised model can be formulated as:
Y = f(X) + e
Where:
- Y is the output.
- X = (x1,⋯,xp) is a p-dimensional vector of features.
- f represents the mathematical function mapping X to Y.
- e is the random error, independent of X.
The true function f is typically unknown and needs to be estimated or approximated. This formula applies to most data formats (numerical, text, images). For images or text, feature extraction methods are necessary to convert raw data into numerical tabular format. Regardless of the data type, features (X) are mapped to the target (Y) via a learned mathematical function (f).
2.2 Key Steps
The core step of supervised learning involves estimating or learning the function f based on independent samples of paired features and outputs. This data can be represented as (Xi, Yi), i=1,⋯, n, where n is the sample size, and Xi and Yi are the feature and output for the ith sample, respectively. Ideally, the function f should minimize the differences between observed outputs (yobs=Yi) and predicted outputs (ypred = f(Xi)) across all samples.
2.3 Loss Function
The difference between observed and predicted outputs is formally defined by a loss function. For regression models, the quadratic loss function is common:
∑ i=1n(yobs−ypred)2=∑ i=1n(Yi−f(Xi))2
This is proportional to the mean squared error (MSE):
MSE= 1n∑ i=1n(Yi−f(Xi))2
MSE is easily interpretable and provides a good balance between bias and variance when optimized.
For classification models, the cross-entropy loss is frequently used:
−∑ i=1n[yobs logypred+(1−yobs)log(1−ypred)]
This is also known as the negative log likelihood and is typically used with the softmax function, a common activation function in deep learning image classification tasks.
2.4 Model Evaluation
Once a loss function is chosen, it must be minimized with respect to f, resulting in the estimated or learned ML model (denoted as f^). To deploy the model for future predictions, its performance must be evaluated using appropriate statistical measures. These include the coefficient of determination (R2) for regression and the area under the curve (AUC) for classification models using a receiver operating characteristic (ROC) curve.
The choice of performance metrics depends on the specific problem and goals of the model. It’s crucial to understand the limitations of each measure, as no single measure should be used in isolation. Aligning the performance measure with the study goals ensures the most useful information about the model’s true capabilities is obtained.
2.5 Regression vs. Classification
A major difference between statistical performance measures in classification and regression models is the type of output each produces. A classification model predicts a categorical outcome (e.g., yes/no), while a regression model predicts a continuous numerical outcome. Consequently, the statistical metrics used to evaluate each model differ.
Classification models use a confusion matrix-based approach to calculate metrics like accuracy, precision, recall, and F1-score. Regression models use mean absolute error, mean squared error, and R2.
3. Statistics of Regression Models
3.1 Common Regression Algorithms
The simplest regression model is simple linear regression, which uses a single feature to predict the dependent variable using a linear function.
3.1.1 Simple Linear Regression
Figure 2A shows a simple linear regression example relating height (feature) to weight (dependent variable). While not commonly used in ML, simple linear regression helps understand statistical performance measures (R2, MSE, etc.) shared across many regression algorithms.
Core elements of this method help visualize and explain the relationships between output and feature variables. For example, examining the relationship between weight and height helps understand these core concepts and model performance measures like R2.
Figure 2A: Illustrates simple linear regression and the calculation of R2, showing how the model fits the data.
In this example, we assess how much weight variation can be explained by height. Can a fitted line correlating weight and height better represent this relationship than a line representing the mean weight? If the summative difference between individual weight and height values from the fitted line is lower than the collective difference of individual weight values from the weight mean, then the fitted line can use height values to explain some weight variations better than the weight mean alone.
Mathematically, this is shown by comparing the “sum of squares of residuals” (SSR) of the mean versus the SSR of the fitted line. If the SSR of the mean is greater than the SSR of the fitted line, height explains some weight variations. The concept of R2 then quantifies how much weight variation is explained by height.
3.1.2 Linear Regression
Linear regression assumes a parametric linear function for the model:
f(X)=β0+β1×1+⋯+βpxp
Where:
- β0 is the intercept.
- βj is the slope associated with feature xj, j = 1,⋯,p.
Estimating the function f involves estimating the unknown parameters β = (β0,⋯,βp). With a single feature (p=1), this reduces to simple linear regression. The most common method to estimate β is to minimize the sum of squared residuals (SSR) or the squared loss:
SSR(β)=∑i=1n(yi−f(Xi))2=∑i=1n(yi−XiTβ)2
The minimization problem has an explicit solution:
β^=(XTX)−1XTY
Where X is the feature matrix of all subjects, and *X**T is its transpose. β^ is called the least-square (LS) estimate. When the random error e* follows a Gaussian distribution N(0, σ2), the least-square estimate is equivalent to the maximum likelihood estimate.
3.1.3 k-Nearest Neighbors (kNN)
The kNN is a non-parametric algorithm that uses the data points closest to the query point to make a prediction. It’s a lazy learning algorithm that doesn’t build a complex model before making a prediction but stores the training data in memory.
When making a prediction for a new query point with feature z, it searches the training data for the k nearest neighbors around z, computes their average, and uses the average as the prediction. k should be a positive integer. Closeness is measured in the feature space excluding the output. Common distance measures include Euclidean Distance, Manhattan Distance, and Minkowski Distance.
For two data points with features x = (x1,⋯,xp) and z = (z1,⋯,zp), the Minkowski Distance is defined as:
(∑ j=1p|xj−zj|q)1q
Where q is the order parameter. q=1 is the Manhattan distance, and q=2 is the Euclidean distance. Once the k closest neighbors are found for z, its prediction is derived as the mean outputs of these neighbors:
f(z)=1k∑i∈Nzyi
Where Nz denotes the set of the k closest neighbors, and yi denotes the outputs of the ith subject in Nz.
The number of nearest neighbors (k) can be selected using cross-validation approaches. The kNN algorithm is appealing for its simplicity, but the fitted line can be jagged, especially when k is small.
3.1.4 Local Polynomial Regression
Local polynomial regression makes no global assumptions about the function f but assumes it is a polynomial function in moving local neighborhoods. It’s based on Taylor’s series expansion. For example, with a univariate feature (p=1), local polynomial regression of order m can be expressed as:
f(X)=∑j=0mαj(X−z)j
For any data X close to z, the query point of interest; α0 = f(z) and αj’s are the unknown coefficients for the other polynomial terms. Local polynomial regression can be estimated by generalizing the least-square estimate for linear regression to minimize the kernel-weighted local sum of squared residuals:
SSR(f, z)=∑i=1nK(Xi, z)(yi−f(Xi))2
Where K(·,·) is a kernel function that assigns weights to training data points. Data points closer to z receive greater weights than those further away. A commonly used kernel is the Gaussian kernel:
K(X, z)=12πσexp(−||X−z||22σ2)
If the function f is assumed constant (m=0) in the neighborhood, the resulting estimate becomes the Nadaraya-Watson estimate. The kNN algorithm can be viewed as a special Nadaraya-Watson estimate, where the kernel function equals 1 for the k nearest neighbors and 0 for other data points. Supplementary Figure 1 shows the fitted lines of the Nadaraya-Watson estimate and local polynomial regression with a degree of 3 (local cubic regression). This method is useful when the underlying data is nonlinear and no applicable parametric model exists. It can also identify local patterns in the data not evident in a global model.
3.1.5 Support Vector Regression (SVR)
Support vector regression (SVR) extends the Support Vector Machine (SVM) algorithm (used for classification problems) to enable regression tasks. SVR uses similar principles as SVM but is used for continuous outputs.
3.1.6 Neural Network Regression
Neural network regression uses a network of artificial neurons that may use techniques like back-propagation, dropout, and adaptive learning to adjust weights and thresholds to achieve desired accuracy. Weights and thresholds are adjusted using formulas like Gradient Descent, Adam Optimizer, and root mean squared error. These formulas calculate the error between predicted and actual values and update weights and thresholds accordingly. Neural network regression is effective for predicting continuous values with great accuracy.
3.2 Performance Metrics for Regression
Common statistical measures for evaluating regression performance include Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), R2, and adjusted R2.
3.2.1 Mean Absolute Error (MAE)
The Mean Absolute Error (MAE), related to the L1 loss, is the average absolute difference between predicted and observed (true) outputs. It’s calculated as:
MAE=1n∑ i=1n|yi−y^i|
Where yi and y^i=f^(Xi) represent the observed (true) and predicted outputs for the ith sample, respectively.
3.2.2 Mean Squared Error (MSE)
The Mean Squared Error (MSE), also known as the L2 loss, is calculated as the sum of the squared differences between predicted and observed outputs, divided by the number of samples:
MSE=1n∑ i=1n(yi−y^i)2
MSE is more sensitive to outliers than MAE because it penalizes large errors more heavily.
3.2.3 Root Mean Squared Error (RMSE)
Root Mean Squared Error (RMSE), also known as the root mean squared deviation, is the square root of the MSE. It is commonly used because it has the same units as the original data, making it easier to interpret.
MSE or RMSE can compare the performance of different regression models, with lower values indicating a better fit. However, they are sensitive to the scale of the target variable and are generally not applicable for comparing models with different target variables.
3.2.4 R2 (Coefficient of Determination)
R2 is the coefficient of determination, defined as:
R2=1−SSRSSmean=1− ∑i=1n(yi− y^i)2∑i=1n(yi−y¯)2
Where:
- y¯=1n∑ i=1nyi is the mean of all observed outputs.
- SSmean=∑ i=1n(yi−y¯)2 is the sum of squares of the mean (Figure 2A), equivalent to the sum of squared residuals from the sample mean.
Since SSmean is always greater than or equal to SSR, R2 has a value between 0 and 1. It can be interpreted as the proportion of the target variable’s variance that is explained by the features in the model.
Figure 2A: Shows linear regression and related statistics, emphasizing R2 calculation and its importance.
In the case of a single feature, R2 is the square of the Pearson correlation coefficient between the output and the feature. An R2 of 0 indicates that the model does not explain any of the variance in the output variable, and a value of 1 indicates that the model explains all of the variance.
R2 is useful for assessing the overall fit of a regression model, while MAE, MSE, and RMSE are more useful for assessing the performance of a model on a particular dataset. One limitation of R2 is that it increases when extra features are added to the model, making it less useful for comparing models with nested sets of features.
3.2.5 Adjusted R2
Adjusted R2 is a modification to account for the issue of R2 increasing with added features:
Radj2=1−SSRn−p−1SSmeann−1
Where n–p-1 and n-1 are the degrees of freedom for SSR and SSmean, respectively. Adjusted R2 penalizes models for adding features not related to the output variable, making it less biased than R2. The value of Radj2 is always less than or equal to R2.
3.3 Bias and Variance Trade-off and Regularization
The bias-variance trade-off is a central concept in supervised ML studies. It states that an algorithm’s ability to generalize to unseen data is a trade-off between its complexity (variance) and its bias.
Bias refers to the error introduced by simplifying the model, while variance refers to the error introduced by making the model too complex. An algorithm with low bias is generally more complex (increased variance) and more likely to overfit the training data. Conversely, an algorithm with high bias (low variance) may be too simple and more likely to underfit the training data.
Figure 2B: Depicts the bias and variance trade-off, illustrating how model complexity affects prediction accuracy.
Mathematically, for the query data point with feature z, the true and predicted outputs are f(z) and f^(z), respectively, and the total expected error can be expressed as:
E(f(z)−f^(z))2=E(f(z)−Ef^(z)+Ef^(z)−f^(z))2=(Ef^(z)−f(z))2+Var(f^(z))=bias2+variance
The first term represents the squared bias, and the second term represents the variance of the prediction itself. As the model becomes more complex, the bias is reduced, but the variance increases. Thus, the model deviates from the optimal spot with the lowest total prediction error.
One popular method to balance bias and variance is regularization. Regularization addresses the bias-variance trade-off by adding a penalty to the loss function of a model to reduce its variance at a sacrifice of a small amount of bias. Mathematically, regularization for regression can be formulated as minimizing the penalized sum of squared residuals:
∑i=1n(yi−f(xi))2+λR(β)
Where:
- λ is the tuning parameter.
- R(β) is a penalty term.
Three common penalty terms in practice:
- L2 norm of the parameters with R(β)=∑ j=1pβj2 for ridge regression
- L1 norm with R(β)=∑ j=1p|βj| for least absolute shrinkage and selection operator (LASSO)
- A combination of L1 and L2 norms as λ1∑ j=1p|βj|+λ2∑ j=1pβj2 for elastic net
Figure 2C: Shows the regularization concept, pre- and post-regularization of fitted lines, demonstrating improved generalization.
The lambda parameters can be selected with cross-validation. When LASSO or elastic net is used, some regression coefficients may be shrunken to zero, effectively serving as feature selection procedures.
Regularization can improve the generalization of a model, making it more resilient to overfitting. As shown in Figure 2C, a model without regularization fits the training data well but has large prediction errors when applied to testing data. After regularization, the model achieves more balanced performance, though the bias is larger for the training data.
Other methods for optimizing the bias-variance trade-off in supervised learning tasks include the use of ensemble techniques, early stopping, and feature selection. Additionally, hyperparameter tuning with cross-validation tasks can reduce overfitting and improve the generalization performance of an ML model.
4. Statistics of Classification
4.1 Common Classification Algorithms
4.1.1 Logistic Regression
Logistic regression is not typically used in image or text classification tasks but is one of the most popular methods for classification within the tabular data domain. It predicts the probability of the output (e.g., the probability that a patient has cancer based on features like age, blood pressure, and genomic mutations). The model estimates the probability using the logistic function:
P(X)=exp(β0+β1X1+⋯+βpXp)1+exp(β0+β1X1+⋯+βpXp)=11+exp(−XTβ)
Where:
- P(X) is the probability of the outcome occurring (e.g., cancer diagnosis).
- X = (X1,⋯,Xp) and β = (β1,⋯,βp) are the features and associated parameters, as in linear regression.
An equivalent transformation of the logistic model expresses it in terms of log-transformed odds:
logP(X)1−P(X)=β0+β1X1+⋯+βpXp
Where each β parameter can be interpreted as a log-odds ratio of the associated feature, a measurement widely used in medicine. If the output is a multi-class (more than two classes) variable, the logistic model has two common extensions: multinomial logistic regression and ordinal logistic regression. The latter is tailored to output variables whose classes have a natural order (e.g., mild, moderate, and severe conditions).
Figure 3A: Logistic Regression, demonstrating how the model estimates probabilities for binary outcomes.
4.1.2 k-Nearest-Neighbors (kNN)
The kNN algorithm can be used for both regression and classification tasks. This is a type of instance-based learning where the model is trained by storing the grouped training data and making predictions based on the k nearest neighbors. To make a prediction for a new sample, the algorithm calculates the distance between the new sample and each stored training sample based on their features and determines the k closest samples. The prediction is then based on the majority class of the k nearest neighbors.
Figure 3B: Shows how k-Nearest Neighbor Classification works with k=3, illustrating class prediction based on proximity.
4.1.3 Naïve Bayes
Naïve Bayes classifiers are a collection of classification algorithms that use Bayes’ theorem. Following Bayes’ theorem, the conditional probability of the output Y given the feature X = (X1,⋯,Xp) can be written as:
p(Y|X)=p(Y,X)p(X)=p(X|Y)p(Y)p(X)
The naïve Bayes methods assume that the features are independent of each other. Under this assumption, the expression can be further decomposed as:
p(Y|X)=p(X|Y)p(Y)p(X)=p(X1|Y)…p(Xp|Y)p(Y)p(X1)…p(XP)
Different naïve Bayes classifiers differ mainly in the distribution of the features given the output (i.e., p(Xj|Y), j = 1,⋯,p). Common classifiers include Gaussian naïve Bayes, multinomial naïve Bayes, and Bernoulli naïve Bayes classifiers. Despite the incorrect assumption of features being independent of each other, naïve Bayes classifiers can sometimes produce reasonable results, especially for simple tasks. However, their performance has been shown to be inferior to some other well-established algorithms for more complex tasks.
4.1.4 Decision Tree Based Methods
These methods can be used for both classification and regression tasks. A decision tree is a model that partitions the feature space into distinct regions hierarchically. A classification decision tree starts with a root node, which is divided into a left child and a right child. Each child node is further split to create successive partitions. A child node that cannot be subdivided is called a leaf node, where the final class label is assigned.
The construction of a tree requires determining the feature to split and the split cut-off value at each node, a termination rule, and how to label each terminal node. Impurity measures such as cross-entropy and the Gini index are common criteria for determining these elements. Once a tree is constructed, predictions can be made by following the set of split rules from the root to the leaves. The size of the tree (the number of nodes) represents the model’s complexity. A very large tree may overfit the data, requiring tree pruning.
Figure 3C: Illustrates Random Forest Classification, highlighting the ensemble approach and decision-making process.
A single classification tree is rarely used in practice because it can be highly variable. More advanced tree-based methods may overcome these limitations, including ensemble methods such as the bootstrap aggregating (bagging) approach, random forest (RF), and gradient boosting machine (GBM). Bagging constructs a large number of trees with bootstrapped samples from the data, and a classification is made by aggregating the results from individual trees based on a majority vote.
Random forest is very similar to bagging. RF grows trees by introducing randomness to the modeling process. Before each node is split, RF randomly selects a subset of features as candidates instead of searching all features. This introduces wider diversity, and the trees in RF become more independent than those in bagging.
Boosting is another powerful ensemble method. Unlike bagging and RF, which construct a larger number of trees in parallel, boosting (as seen in GBM) creates multiple trees sequentially. Each tree is grown based on the information from previously grown trees (weak learners) to reduce the errors from the previous trees, which can ultimately lead to a better-performing model (a boosted tree). Boosting sometimes yields reasonable models, especially for unbalanced data sets. However, their limited number of tuning parameters may sometimes make boosting more prone to overfitting compared to RF, which uses more parameters for tuning and model optimization.
4.1.5 Support Vector Machine (SVM)
The central idea of support vector machines is to identify a hyperplane as a boundary to separate the output classes as widely as possible. When there are only two features, the separating hyperplane reduces to a linear line.
Separation is maximized by increasing the margin on either side of the line. However, in many cases, it is impossible to find a linear hyperplane that perfectly separates the two output classes in the original feature space. A powerful highlight of SVM is projecting the data into a higher dimensional space using a nonlinear kernel (a mathematical “function”) and then searching for a separating hyperplane in the newly projected space. The resulting hyperplane will be nonlinear when transformed back to the original feature space. This classic use case of Kernels (e.g., the RBF kernel) enhances the algorithm’s capability of finding a linear decision boundary for tasks that would have otherwise not been separable in lower dimensions.
Figure 3D: Illustrates Support Vector Machine Classification, showing how hyperplanes separate classes with maximum margin.
The overall process may also help improve the final model’s performance through separability, dimensionality reduction, regularization, and computational efficiency.
Common choices of the kernel function in SVMs include:
- Polynomial kernel with order q: K(x, x′)=(1 + 〈x, x′〉)q
- Radial basis kernel: K(x, x′)=exp(−γ||x−x′||2)
- Neural network kernel: K(x, x′)=tanh(k1||x−x′||+k2)
SVM can yield highly accurate predictions using flexible kernel functions. By introducing a cost parameter to loosen the perfectness of separation, SVM is also relatively robust to outliers. However, training SVMs could be computationally expensive on large datasets. It can also be viewed as a black-box approach (especially incorporating certain kernels) since the separation of classes may not be intuitive.
4.1.6 Neural Network
Neural networks are increasingly used in both regression and classification tasks. These are inspired by the structure and interplays between human neurons and typically include an input layer (receiving raw input data), hidden layers, and an output layer (producing the final output of the model). Two major neural networks used regularly within medicine include the Multilayer Perceptron (MLP) and the Convolutional Neural Network (CNN). MLPs are typically used for tasks involving structured data (tabular numerical data), while CNNs are better suited for tasks involving unstructured data, such as images for classification or object detection tasks. These CNN deep neural network approaches are sometimes referred to as deep learning.
4.2 Convolutional Neural Networks and Object Detection
A CNN is a special neural network with different specific layers (input layer, convolutional layer, pooling layer, and fully connected layer).
Figure 4A: Demonstrates the Convolutional Neural Network Architecture Concept, highlighting layer functionalities.
The convolutional layer is the core building block of the CNN, and there could be a series of convolutional layers present. When stacked on top of each other, convolutional layers can detect a hierarchy of imaging features and patterns. These features are then pooled and fed into the fully connected layers of artificial neurons for various classification tasks.
Although these black-box neural network methods may be hard to understand, their inner workings are based on traditional statistical concepts. For example, in a CNN, the logit function (sigmoid function) is used to map the input values to a 0 to 1 range and typically serves as the last step before the final output of a CNN. This function is used to calculate the probability of each class and to assign the class (e.g., class 0 or class 1) with the highest probability to the final output. The logit function in a CNN and the logistic regression algorithm are related because both use the logistic function (sigmoid function), which enables both to acquire and assign the relationship between input variables and the output variable.
In recent years, with the development of deep learning, CNN-based models have made great breakthroughs and have become the gold standard for most image-based tasks. Image-based ML tasks can be categorized as image classification, image generation, object detection, and image segmentation.
4.2.1 Image Classification
Image classification involves training a neural network to assign an input image to a specific class or category based on the whole image. For example, an image classification model might be trained to recognize various types of cancer (colon, breast, and prostate cancer). The model would be trained on a large dataset of labeled images from colon, breast, and prostate cancer, allowing the CNN to learn and recognize patterns and features in the images that are characteristic of each assigned class (colon, breast, and prostate). The end result is a trained model that can classify new images based on their shared characteristics to the labeled target class.
4.2.2 Object Detection
Object detection is related to image classification, but its goal is to identify and locate objects within an image (rather than a global analysis or classification of the image). This involves identifying the location and bounding box of each object in the image, as well as classifying each object into a specific class. An example of an object detection model within medicine is one that can detect and identify various individual white blood cells (e.g., neutrophils, lymphocytes, monocytes, eosinophils, and basophils) in the peripheral blood.
Performance measures for object detection and image classification have some similarities but also have some key differences. Additionally, the type of image classification (binary versus multi-class) may also influence certain performance measures, which will need to be accounted for.
4.3 Performance Metrics for Binary Classification
Regardless of whether it’s an image or tabular data task, the performance of a classification model can be evaluated using numeric metrics (e.g., accuracy) along with graphical representations (e.g., the ROC curve).
The performance measures of a classification ML model are derived from a confusion matrix-based approach. A confusion matrix tabulates the predicted outputs as they relate to the observed (true class) outputs, yielding the numbers of true positive, true negative, false positive, and false negative predictions made by the model.
4.3.1 Confusion Matrix Elements
- True Positive (TP): The model correctly predicts that a given sample belongs to a positive class.
- True Negative (TN): The model correctly predicts that a given sample belongs to a negative class.
- False Positive (FP): The model incorrectly predicts that a given sample belongs to a positive class when it actually belongs to a negative class.
- False Negative (FN): The model incorrectly predicts that a given sample belongs to a negative class when it actually belongs to a positive class.
These numbers are then used to calculate statistical performance measures (accuracy, precision, sensitivity, specificity, F1, etc.) that display the model’s ability to distinguish between positive and negative cases.
4.3.2 Key Metrics
- Accuracy: The percentage of correct predictions (TP + TN) / (TP + TN + FP + FN). While accuracy is intuitive, it has a major drawback for imbalanced datasets, where one output class is much more common than the other. In this case, accuracy mainly depends on the performance for the biggest output class, and a naïve model that predicts all data into the dominant class could display high accuracy.
- Balanced Accuracy: A better alternative for imbalanced datasets, giving equal weights to the classes. It is defined as an average of the percentages of correct predictions in each class.
Table 1: Evaluation metrics for binary classification based on the confusion matrix, detailing calculations and interpretations.
Other metrics directly computed from the confusion matrix include sensitivity (positive recall or true positive rate), specificity (true negative rate), positive predictive value (PPV, precision), and negative predictive value (NPV), each measuring a particular aspect of the model’