How To Learn Division: A Comprehensive Guide For All

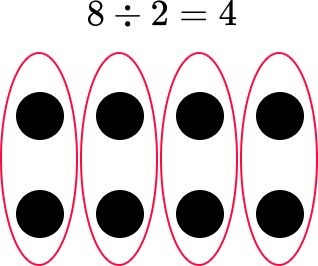
Learning how to learn division effectively is a fundamental skill in mathematics, essential for success in various academic and real-life scenarios. This guide, brought to you by LEARNS.EDU.VN, offers a detailed exploration of division, from basic concepts to advanced techniques, ensuring a solid understanding for learners of all ages. Discover effective division strategies and unlock your mathematical potential.

1. Understanding the Basics of Division

1.1 What is Division?

Division is a fundamental arithmetic operation that involves splitting a whole into equal parts or groups. It’s the inverse operation of multiplication, and it helps us determine how many times one number (the divisor) is contained within another number (the dividend). Mastering division unlocks doors to more complex mathematical concepts and practical problem-solving scenarios.

1.2 Key Terminology

Dividend: The number being divided.
Divisor: The number by which the dividend is divided.
Quotient: The result of the division.
Remainder: The amount left over when the dividend cannot be divided evenly by the divisor.

A helpful way to remember these terms is the formula: Dividend ÷ Divisor = Quotient + Remainder

Understanding these terms is essential for grasping the mechanics of division and applying them effectively.

1.3 Division Symbols and Notation

Division can be represented using several symbols:

÷ (division symbol)
/ (slash)
— (fraction bar)

For example, 10 ÷ 2 = 5, 10 / 2 = 5, and 10/2 = 5 all represent the same division operation. Familiarity with these symbols is crucial for interpreting and solving division problems.

1.4 The Relationship Between Division and Multiplication

Division and multiplication are inverse operations, meaning one undoes the other. This relationship is crucial for understanding and verifying division problems. For example:

If 6 x 4 = 24, then 24 ÷ 6 = 4 and 24 ÷ 4 = 6.

This inverse relationship allows us to check our division answers by multiplying the quotient by the divisor to see if it equals the dividend.

2. Foundational Skills for Learning Division

2.1 Number Sense

Number sense is an intuitive understanding of numbers and their relationships. It includes the ability to:

Estimate quantities
Compare numbers
Understand place value
Recognize number patterns

A strong number sense provides a solid foundation for understanding division. For instance, recognizing that 25 is a quarter of 100 can simplify division problems involving percentages.

2.2 Skip Counting

Skip counting involves counting by multiples of a number. It’s a valuable skill for understanding multiplication and division. For example:

Skip counting by 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…

This skill helps in division by allowing one to quickly determine how many times a divisor fits into a dividend.

2.3 Multiplication Facts

Mastery of multiplication facts is essential for efficient division. Knowing multiplication tables allows one to quickly recall the relationship between numbers, making division problems easier to solve. For example:

Knowing that 7 x 8 = 56 makes it easier to solve 56 ÷ 7 = 8.

Regular practice and memorization of multiplication facts significantly improve division skills.

2.4 Understanding Place Value

Place value is the understanding that the position of a digit in a number determines its value. This is particularly important when dealing with larger numbers in division. For example:

In the number 345, the 3 represents 300, the 4 represents 40, and the 5 represents 5.

Understanding place value allows you to break down larger numbers into smaller, manageable parts during division.

3. Basic Division Methods

3.1 Equal Sharing

Equal sharing is a simple and intuitive method for introducing division, especially for young learners. It involves distributing a set of objects equally among a certain number of groups. For example:

Sharing 12 cookies among 3 friends means each friend gets 4 cookies (12 ÷ 3 = 4).

This method helps children understand division as a fair distribution process.

3.2 Repeated Subtraction

Repeated subtraction involves subtracting the divisor from the dividend until you reach zero or a remainder. The number of times you subtract is the quotient. For example:

To solve 15 ÷ 3:
- 15 – 3 = 12
- 12 – 3 = 9
- 9 – 3 = 6
- 6 – 3 = 3
- 3 – 3 = 0
You subtracted 3 five times, so 15 ÷ 3 = 5.

This method reinforces the concept of division as repeated grouping.

3.3 Using Arrays

Arrays are visual representations of multiplication and division using rows and columns. In division, an array helps to visualize how many groups of a certain size can be made from a total quantity.

For example, to solve 20 ÷ 5 using an array:

Create an array with 20 objects arranged in rows of 5.
Count the number of rows to find the quotient (in this case, 4).

3.4 Area Models

Area models are rectangular diagrams that visually represent the division process. They are particularly useful for dividing larger numbers. The area model represents the total area that the shape takes up. When using this model for multiplication, you would multiply the length by the width to find the area. However, when using the area model for division, you are given the total area (dividend), and the width (divisor), and you will need to calculate the length (quotient).

4. Understanding Remainders

4.1 What is a Remainder?

A remainder is the amount left over when a dividend cannot be divided evenly by the divisor. It represents the portion that does not fit into a whole number of groups.

4.2 Interpreting Remainders

The interpretation of a remainder depends on the context of the problem. For example:

Sharing Situation: If you have 25 stickers to share among 6 friends, each friend gets 4 stickers, and there is 1 sticker left over.
Grouping Situation: If you need to pack 25 books into boxes that hold 6 books each, you can fill 4 boxes completely, and there will be 1 book left over.

4.3 Representing Remainders

Remainders can be represented in several ways:

As a whole number: 25 ÷ 6 = 4 R 1 (R stands for remainder)
As a fraction: 25 ÷ 6 = 4 1/6
As a decimal: 25 ÷ 6 ≈ 4.167

The choice of representation depends on the level of precision required.

5. Long Division: A Step-by-Step Guide

5.1 Introduction to Long Division

Long division is a method for dividing large numbers by breaking down the process into smaller, manageable steps. It’s particularly useful when dividing numbers with multiple digits. The standard algorithm, or long division, is a method that is used when dividing a large number (usually three digits or more) by a single- or multi-digit number.

5.2 Steps for Long Division

Here are the steps for performing long division:

Set up the problem: Write the dividend inside the division bracket and the divisor outside.
Divide: Determine how many times the divisor goes into the first digit (or first few digits) of the dividend.
Multiply: Multiply the quotient by the divisor.
Subtract: Subtract the product from the corresponding digits of the dividend.
Bring Down: Bring down the next digit of the dividend.
Repeat: Repeat steps 2-5 until all digits of the dividend have been used.
Remainder: If there is a remainder, write it as R followed by the remaining number.

5.3 Example of Long Division

Let’s divide 528 by 24 using long division:

      22
    ------
24 | 528
   - 48
   ------
     48
   - 48
   ------
     0

Divide: 24 goes into 52 two times.
Multiply: 2 x 24 = 48.
Subtract: 52 – 48 = 4.
Bring Down: Bring down the 8 to make 48.
Repeat: 24 goes into 48 two times.
Multiply: 2 x 24 = 48.
Subtract: 48 – 48 = 0.

Therefore, 528 ÷ 24 = 22.

5.4 Tips for Long Division

Estimate: Estimate the quotient before starting to ensure your answer is reasonable.
Neatness: Keep your work organized to avoid errors.
Check: Multiply the quotient by the divisor to verify your answer.

6. Dividing by Multi-Digit Divisors

6.1 Understanding Multi-Digit Divisors

Dividing by multi-digit divisors can seem daunting, but the same principles of long division apply. The key is to break down the problem into smaller steps and use estimation. The key when it comes to the standard algorithm for kids is to go slow and encourage them to present their work neatly so that they can spot mistakes easily and work to rectify them.

6.2 Steps for Dividing by Multi-Digit Divisors

Set up the problem: Write the dividend and divisor in the long division format.
Estimate: Estimate how many times the divisor goes into the first few digits of the dividend.
Multiply: Multiply the estimated quotient by the divisor.
Subtract: Subtract the product from the corresponding digits of the dividend.
Bring Down: Bring down the next digit of the dividend.
Repeat: Repeat steps 2-5 until all digits of the dividend have been used.
Remainder: Write the remainder as needed.

6.3 Example: Dividing by a Two-Digit Divisor

Here’s an example of dividing 1456 by 32:

       45 R 16
    ----------
32 | 1456
   - 128
   -------
     176
   - 160
   -------
      16

Estimate: 32 goes into 145 four times.
Multiply: 4 x 32 = 128.
Subtract: 145 – 128 = 17.
Bring Down: Bring down the 6 to make 176.
Repeat: 32 goes into 176 five times.
Multiply: 5 x 32 = 160.
Subtract: 176 – 160 = 16.
Remainder: The remainder is 16.

Therefore, 1456 ÷ 32 = 45 R 16.

7. Dividing with Decimals

7.1 Understanding Decimal Division

Dividing with decimals involves dividing a number by a decimal or dividing a number into a decimal. The standard algorithm will be used for numbers involving decimals for the first time in upper elementary. This means that it is a good time to revise place value so that your child understands how decimals work.

7.2 Dividing a Decimal by a Whole Number

To divide a decimal by a whole number, perform long division as usual, but bring the decimal point straight up from the dividend to the quotient.

7.3 Dividing by a Decimal

To divide by a decimal, you need to convert the divisor into a whole number by multiplying both the divisor and dividend by a power of 10. Then, perform long division as usual.

7.4 Example of Decimal Division

Let’s divide 4.25 by 5:

      0.85
    ------
5 | 4.25
   - 4.0
   ------
     0.25
   - 0.25
   ------
      0

Therefore, 4.25 ÷ 5 = 0.85.

8. Real-Life Applications of Division

8.1 Practical Examples

Division is used in many real-life situations, including:

Sharing costs: Dividing a restaurant bill among friends.
Calculating averages: Finding the average test score.
Converting units: Converting kilometers to miles.
Baking: Adjusting ingredient quantities in a recipe.
Finance: Calculating monthly payments on a loan.

8.2 Word Problems

Word problems help to apply division skills in context. For example:

“A baker makes 144 cookies and wants to pack them into boxes of 12. How many boxes does she need?” (144 ÷ 12 = 12 boxes)
“A school has 350 students, and each classroom can hold 25 students. How many classrooms are needed?” (350 ÷ 25 = 14 classrooms)

Solving word problems enhances problem-solving skills and demonstrates the practical relevance of division.

9. Common Mistakes and How to Avoid Them

9.1 Misunderstanding Place Value

A common mistake is misaligning digits during long division, leading to incorrect calculations. To avoid this, ensure that digits are lined up correctly according to their place value.

9.2 Forgetting to Bring Down

Skipping the “bring down” step can lead to incomplete division. Always remember to bring down the next digit of the dividend after each subtraction.

9.3 Incorrect Multiplication Facts

Errors in multiplication facts can significantly impact division results. Regularly review and practice multiplication tables to minimize these errors.

9.4 Not Checking the Answer

Failing to check the answer can result in undetected mistakes. Always multiply the quotient by the divisor to verify that it equals the dividend (plus the remainder, if any).

10. Advanced Division Techniques

10.1 Dividing by Powers of 10

Dividing by powers of 10 (10, 100, 1000, etc.) is simplified by moving the decimal point to the left. The number of places you move the decimal point is equal to the number of zeros in the power of 10. For example:

450 ÷ 10 = 45 (move the decimal point one place to the left)
450 ÷ 100 = 4.5 (move the decimal point two places to the left)

10.2 Estimation and Approximation

Estimation and approximation are useful for quickly determining an approximate answer. Round the dividend and divisor to the nearest whole number or convenient value, and then perform the division. This provides a rough estimate that can be refined as needed.

10.3 Mental Division Strategies

Mental division involves performing division calculations in your head without the aid of paper or a calculator. This requires strong number sense, quick recall of multiplication facts, and the ability to break down numbers into manageable parts.

11. Resources for Learning Division

11.1 Online Tools and Websites

Numerous online resources can aid in learning division:

Khan Academy: Offers free video lessons and practice exercises on division and other math topics.
Math Playground: Provides interactive math games and activities that make learning division fun.
LEARNS.EDU.VN: Offers comprehensive educational resources and personalized learning paths for mastering division.

11.2 Workbooks and Textbooks

Workbooks and textbooks provide structured lessons and practice problems. Look for resources that offer step-by-step explanations and a variety of exercises to reinforce learning.

11.3 Apps

Educational apps can make learning division engaging and accessible:

Prodigy Math: A game-based learning platform that adapts to the student’s skill level.
SplashLearn: Offers interactive math games and activities aligned with curriculum standards.
Math Workout: Provides targeted practice on various math skills, including division.

12. Making Division Fun and Engaging

12.1 Games

Turn division practice into a game with activities like:

Division Bingo: Create bingo cards with division problems and call out the answers.
Division Flashcards: Use flashcards to quiz division facts and make it a timed competition.
Online Division Games: Explore interactive division games on websites like Math Playground and Coolmath Games.

12.2 Real-World Activities

Engage in real-world activities that involve division, such as:

Baking: Measure ingredients and divide them equally among portions.
Sharing: Divide snacks or toys among friends or family members.
Planning: Calculate the cost per person for a group outing.

12.3 Visual Aids

Use visual aids to illustrate division concepts:

Arrays: Arrange objects in rows and columns to visualize division problems.
Area Models: Draw rectangular diagrams to represent division.
Number Lines: Use number lines to demonstrate repeated subtraction.

13. Division for Different Learning Styles

13.1 Visual Learners

Visual learners benefit from visual aids such as arrays, area models, and diagrams. Encourage them to draw pictures and use color-coding to organize their work.

13.2 Auditory Learners

Auditory learners learn best through listening. Encourage them to verbalize division problems and solutions, listen to instructional videos, and participate in discussions.

13.3 Kinesthetic Learners

Kinesthetic learners learn through hands-on activities. Provide them with manipulatives such as counters, blocks, and base-ten blocks to physically represent division problems.

14. How LEARNS.EDU.VN Can Help You Master Division

LEARNS.EDU.VN is dedicated to providing comprehensive and accessible educational resources to help learners of all ages master division. Our platform offers:

Detailed lessons: Step-by-step explanations of division concepts and techniques.
Practice exercises: A wide range of practice problems to reinforce learning.
Personalized learning paths: Customized learning plans tailored to individual needs and goals.
Expert support: Access to experienced educators who can provide guidance and answer questions.

15. Encouraging a Growth Mindset

15.1 Emphasize Effort Over Ability

Encourage learners to focus on effort and persistence rather than innate ability. Emphasize that division is a skill that can be developed through practice and hard work.

15.2 Embrace Mistakes as Learning Opportunities

Frame mistakes as valuable learning opportunities. Encourage learners to analyze their errors, identify areas for improvement, and try again.

15.3 Celebrate Progress

Acknowledge and celebrate progress, no matter how small. Recognize effort, persistence, and improvement to foster a positive attitude towards learning division.

By following this comprehensive guide and utilizing the resources available at LEARNS.EDU.VN, you can master division and build a solid foundation for future mathematical success.

16. Division and Its Role in Higher Mathematics

16.1 Algebra

Division is fundamental in algebra, especially when solving equations. Algebraic equations often require isolating a variable, which frequently involves division. For instance, in the equation 3x = 15, you divide both sides by 3 to find x = 5. Understanding division is essential for manipulating equations and solving for unknowns.

16.2 Calculus

In calculus, division is used extensively in evaluating limits, finding derivatives, and integrating functions. For example, the quotient rule is a key concept for differentiating a function that is the ratio of two other functions. Division is also crucial in understanding rates of change and optimization problems.

16.3 Geometry

Division is used in geometry to calculate ratios, proportions, and scaling factors. For example, when determining the similarity of triangles, you often need to divide corresponding sides to check if they are in proportion. Division is also used in calculating areas and volumes of various geometric shapes.

16.4 Statistics

In statistics, division is used to calculate averages, probabilities, and other key metrics. For example, the mean (average) of a set of numbers is calculated by dividing the sum of the numbers by the count of the numbers. Understanding division is crucial for interpreting and analyzing statistical data.

17. The Cultural and Historical Significance of Division

17.1 Ancient Civilizations

Division has been used since ancient times for various practical purposes. Ancient civilizations like the Egyptians and Babylonians used division for land surveying, taxation, and trade. The Rhind Papyrus, an ancient Egyptian mathematical document, contains several problems involving division.

17.2 Development of Algorithms

The development of efficient division algorithms has been a significant milestone in the history of mathematics. The long division algorithm, as we know it today, evolved over centuries and was refined by mathematicians from different cultures.

17.3 Modern Computing

Division is a fundamental operation in modern computing. Computer processors perform division using complex algorithms to ensure accuracy and efficiency. Division is used in a wide range of applications, from scientific simulations to financial calculations.

18. The Future of Division Education

18.1 Technology Integration

The future of division education will likely involve increased integration of technology. Interactive simulations, adaptive learning platforms, and educational apps can provide personalized learning experiences and make division more engaging for students.

18.2 Personalized Learning

Personalized learning approaches will become more prevalent, allowing students to learn at their own pace and focus on areas where they need the most support. Adaptive learning platforms can track student progress and adjust the difficulty of problems accordingly.

18.3 Real-World Applications

Future division education will emphasize real-world applications to make the subject more relevant and meaningful. Students will engage in problem-solving activities that require them to apply division skills to solve practical problems.

19. Addressing Math Anxiety Related to Division

19.1 Understanding Math Anxiety

Math anxiety is a feeling of tension, apprehension, or fear that interferes with math performance. It can affect students of all ages and can hinder their ability to learn and apply mathematical concepts, including division.

19.2 Strategies to Reduce Math Anxiety

Create a Positive Learning Environment: Foster a supportive and encouraging learning environment where students feel comfortable asking questions and making mistakes.
Start with Concrete Examples: Begin with concrete examples and hands-on activities to build a solid understanding of division concepts before moving to more abstract problems.
Break Down Complex Problems: Break down complex division problems into smaller, more manageable steps to reduce feelings of overwhelm.
Use Visual Aids: Use visual aids such as arrays, area models, and diagrams to help students visualize division problems and make them more concrete.
Practice Relaxation Techniques: Teach students relaxation techniques such as deep breathing and visualization to help them manage anxiety during math tasks.
Encourage Positive Self-Talk: Encourage students to use positive self-talk to challenge negative thoughts and build confidence in their math abilities.

19.3 Seeking Professional Help

If math anxiety is severe or persistent, it may be helpful to seek professional help from a therapist or counselor who specializes in anxiety disorders.

20. Frequently Asked Questions (FAQs) About Learning Division

Q1: What is the best age to start learning division?

A: Children typically begin learning the basics of division in the 3rd grade (around age 8), but foundational skills can be introduced earlier.

Q2: What are some common difficulties students face when learning division?

A: Common difficulties include misunderstanding place value, forgetting multiplication facts, and difficulty with long division steps.

Q3: How can I help my child with division homework?

A: Provide a quiet study environment, review the steps for division, offer encouragement, and break down problems into smaller steps.

Q4: Are there any online resources that can help with learning division?

A: Yes, Khan Academy, Math Playground, and LEARNS.EDU.VN are excellent online resources.

Q5: How can I make division more fun for my child?

A: Use games, real-world activities, and visual aids to make division more engaging and enjoyable.

Q6: What is the difference between short division and long division?

A: Short division is a simplified method for dividing smaller numbers, while long division is used for larger numbers with multiple digits.

Q7: How do I divide a number by a decimal?

A: Convert the divisor into a whole number by multiplying both the divisor and dividend by a power of 10, then perform long division.

Q8: What is a remainder in division?

A: A remainder is the amount left over when the dividend cannot be divided evenly by the divisor.

Q9: How do I check my answer in a division problem?

A: Multiply the quotient by the divisor and add the remainder (if any). The result should equal the dividend.

Q10: How can LEARNS.EDU.VN help me improve my division skills?

A: LEARNS.EDU.VN offers detailed lessons, practice exercises, personalized learning paths, and expert support to help you master division.

Learning division is a journey that requires patience, practice, and the right resources. With the comprehensive guidance and support offered by LEARNS.EDU.VN, you can unlock your mathematical potential and achieve success in division and beyond. Remember to embrace challenges, celebrate progress, and never stop learning.

Ready to take your division skills to the next level? Visit LEARNS.EDU.VN today for more detailed lessons, practice exercises, and personalized support! Contact us at 123 Education Way, Learnville, CA 90210, United States. Whatsapp: +1 555-555-1212. Website: learns.edu.vn.