How Long to Learn Trigonometry: A Comprehensive Guide

Trigonometry, a branch of mathematics dealing with relationships between the sides and angles of triangles, is essential for various fields. Wondering How Long To Learn Trigonometry? This article from LEARNS.EDU.VN breaks down the learning timeline, effective strategies, and resources to help you master trigonometry efficiently, covering everything from basic concepts to advanced problem-solving techniques. Discover time-saving tips and effective learning methods to optimize your trigonometric journey, ultimately enhancing your mathematical proficiency.

1. Understanding the Foundations of Trigonometry

Trigonometry, at its core, is the study of the relationships between angles and sides of triangles. It builds upon fundamental concepts like geometry and algebra, requiring a solid understanding of these prerequisites to grasp trigonometric principles effectively.

1.1 Essential Prerequisites: Algebra and Geometry

Before diving into trigonometry, ensure you have a firm grasp of basic algebra and geometry concepts. These include:

Algebra: Solving equations, understanding variables, working with functions, and graphing linear equations are crucial.
Geometry: Familiarity with shapes, angles, and especially triangles (right triangles, acute triangles, obtuse triangles) is vital. Understanding the Pythagorean theorem is also fundamental.

Having these basics in place will significantly ease your transition into trigonometry, making the learning process smoother and more efficient. If you’re looking to brush up on these skills, resources like Khan Academy and the math sections on LEARNS.EDU.VN can provide targeted support.

1.2 Core Trigonometric Concepts: Sine, Cosine, and Tangent

The foundational elements of trigonometry revolve around three primary trigonometric functions: sine (sin), cosine (cos), and tangent (tan). These functions relate the angles of a right triangle to the ratios of its sides.

Sine (sin): The ratio of the length of the opposite side to the length of the hypotenuse.
Cosine (cos): The ratio of the length of the adjacent side to the length of the hypotenuse.
Tangent (tan): The ratio of the length of the opposite side to the length of the adjacent side.

These functions are often remembered using the mnemonic SOH CAH TOA:

SOH: Sine = Opposite / Hypotenuse
CAH: Cosine = Adjacent / Hypotenuse
TOA: Tangent = Opposite / Adjacent

Understanding these ratios is essential for solving basic trigonometric problems. To enhance your understanding, LEARNS.EDU.VN provides detailed explanations and practice problems tailored to these core concepts.

1.3 The Unit Circle: A Visual Tool for Trigonometry

The unit circle is a circle with a radius of one, centered at the origin of a coordinate plane. It’s an invaluable tool for visualizing and understanding trigonometric functions beyond acute angles (0 to 90 degrees).

Understanding Angles: Angles are measured counterclockwise from the positive x-axis.
Coordinates and Functions: The x-coordinate of a point on the unit circle corresponds to the cosine of the angle, and the y-coordinate corresponds to the sine of the angle.
Extending Trigonometric Functions: The unit circle allows you to extend the definitions of sine and cosine to all real numbers, not just angles in a right triangle.

By using the unit circle, you can easily determine the sine, cosine, and tangent values for various angles, including those greater than 90 degrees and negative angles. This visual aid is crucial for mastering trigonometry and is thoroughly explained with interactive tools on LEARNS.EDU.VN.

2. Estimating Your Learning Timeline

The duration required to learn trigonometry can vary widely based on several factors. Understanding these factors can help you create a realistic study plan tailored to your individual needs and circumstances.

2.1 Factors Influencing Learning Speed

Several factors influence how quickly you can learn trigonometry:

Prior Math Knowledge: A strong foundation in algebra and geometry significantly reduces learning time.
Learning Style: Visual learners may benefit from diagrams and interactive tools, while auditory learners might prefer lectures and discussions.
Time Commitment: Consistent study habits and dedicated practice sessions accelerate learning.
Resources and Guidance: Access to quality learning materials and expert guidance can streamline the learning process.
Personal Aptitude: Natural aptitude for math can influence how quickly you grasp new concepts.

By recognizing these factors, you can tailor your learning approach to maximize efficiency. LEARNS.EDU.VN offers resources that cater to various learning styles, helping you optimize your study time.

2.2 Time Estimates for Different Levels of Proficiency

Here’s a general timeline for learning trigonometry at different proficiency levels:

Proficiency Level	Description	Estimated Time (Hours)	Activities
Beginner	Understanding basic trigonometric functions (sine, cosine, tangent), solving simple right triangle problems.	20-40	Studying definitions, practicing basic problems, using mnemonic devices, watching introductory videos.
Intermediate	Working with the unit circle, understanding trigonometric identities, solving more complex problems involving angles of elevation and depression.	40-80	Practicing with the unit circle, memorizing identities, solving word problems, working through practice exams.
Advanced	Applying trigonometry to advanced problems, including complex numbers, vectors, and calculus-based applications.	80-150+	Working on challenging problems, exploring advanced topics, applying trigonometry to other fields like physics or engineering, tutoring others.

These estimates are approximate and can vary based on the factors mentioned earlier. Regularly assessing your progress and adjusting your study plan accordingly is crucial. LEARNS.EDU.VN provides tools to track your progress and adapt your learning strategy.

2.3 Creating a Realistic Study Schedule

Developing a structured study schedule is essential for efficient learning. Here are some tips:

Set Specific Goals: Define what you want to achieve in each study session.
Allocate Dedicated Time: Schedule regular study times, even if it’s just for 30 minutes a day.
Break Down Topics: Divide the material into manageable chunks to avoid feeling overwhelmed.
Use a Variety of Resources: Mix textbooks, online tutorials, and practice problems to keep things engaging.
Incorporate Breaks: Short breaks can improve focus and retention.
Review Regularly: Review previously learned material to reinforce your understanding.
Seek Help When Needed: Don’t hesitate to ask questions or seek assistance from teachers, tutors, or online forums.

LEARNS.EDU.VN offers resources to help you create and manage your study schedule effectively, ensuring you stay on track and achieve your learning goals.

3. Effective Learning Strategies for Trigonometry

To master trigonometry, it’s crucial to employ effective learning strategies that cater to your individual needs and learning style. A combination of active learning, consistent practice, and the right resources can significantly enhance your understanding and retention.

3.1 Active Learning Techniques

Active learning involves engaging with the material in a meaningful way, rather than passively reading or listening. Some effective active learning techniques for trigonometry include:

Problem Solving: Work through a variety of problems, starting with basic exercises and gradually progressing to more complex ones.
Teaching Others: Explaining concepts to someone else forces you to solidify your understanding.
Creating Flashcards: Use flashcards to memorize trigonometric identities, formulas, and definitions.
Concept Mapping: Create visual diagrams that illustrate the relationships between different concepts.
Self-Testing: Regularly test yourself to identify areas where you need more practice.
Interactive Simulations: Utilize online simulations to visualize trigonometric functions and their applications.

LEARNS.EDU.VN offers interactive simulations and practice problems designed to promote active learning and deepen your understanding of trigonometry.

3.2 Utilizing Online Resources and Tools

The internet offers a wealth of resources for learning trigonometry. Some valuable online tools and resources include:

Khan Academy: Offers free video lessons and practice exercises covering a wide range of math topics, including trigonometry.
LEARNS.EDU.VN: Provides comprehensive articles, tutorials, and practice problems tailored to different skill levels.
Wolfram Alpha: A computational knowledge engine that can solve trigonometric equations and provide step-by-step solutions.
GeoGebra: A dynamic mathematics software for visualizing geometric constructions and trigonometric functions.
YouTube: Many channels offer trigonometry tutorials and explanations.

These resources can supplement your learning and provide additional support when you encounter challenging concepts. LEARNS.EDU.VN curates a selection of the best online resources to help you succeed in your trigonometry journey.

3.3 Memorization Techniques for Trigonometric Identities

Trigonometric identities are equations that are true for all values of the variables. Memorizing these identities is crucial for solving trigonometric problems efficiently. Some effective memorization techniques include:

Repetition: Repeatedly writing out the identities can help reinforce them in your memory.
Mnemonics: Create memorable phrases or acronyms to help you recall the identities.
Flashcards: Use flashcards to quiz yourself on the identities regularly.
Derivation: Understand how the identities are derived, which can make them easier to remember.
Application: Apply the identities in problem-solving to reinforce your understanding and memory.

LEARNS.EDU.VN provides a comprehensive list of trigonometric identities and offers strategies to help you memorize and apply them effectively.

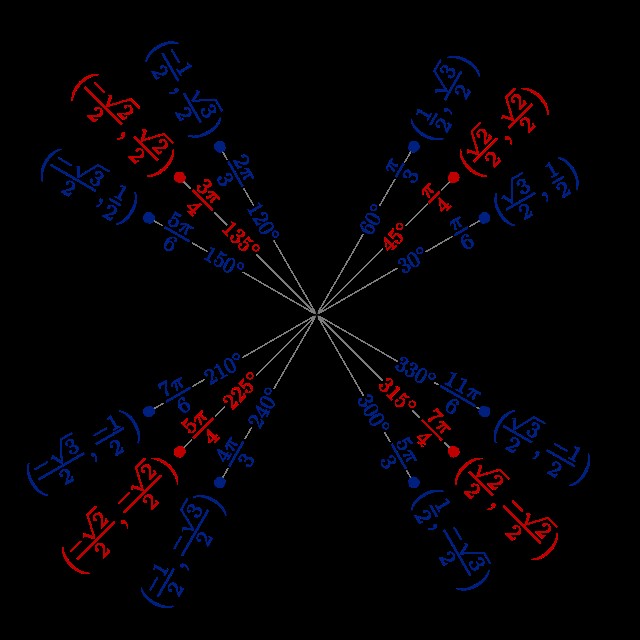Trigonometric Functions on the Unit Circle

3.4 Practice Problems and Their Importance

Consistent practice is essential for mastering trigonometry. Working through a variety of problems helps you apply what you’ve learned and solidify your understanding.

Start with Basic Problems: Begin with simple exercises to build confidence and reinforce fundamental concepts.
Progress to More Complex Problems: Gradually tackle more challenging problems that require you to apply multiple concepts and identities.
Solve Word Problems: Word problems help you apply trigonometry to real-world scenarios.
Review Your Work: Carefully review your solutions to identify areas where you made mistakes and learn from them.
Seek Feedback: Ask teachers, tutors, or classmates to review your work and provide feedback.

LEARNS.EDU.VN offers a wide range of practice problems, from basic exercises to advanced challenges, along with detailed solutions to help you learn effectively.

4. Overcoming Common Challenges in Learning Trigonometry

Learning trigonometry can present several challenges, especially for those who are new to the subject or have gaps in their math foundation. Recognizing these challenges and developing strategies to overcome them is essential for success.

4.1 Dealing with Math Anxiety

Math anxiety is a common issue that can hinder learning. It’s characterized by feelings of stress, fear, or discomfort when faced with mathematical tasks. Here are some strategies to cope with math anxiety:

Identify the Source: Determine what triggers your anxiety and address those specific issues.
Build Confidence: Start with easier problems and gradually work your way up to more challenging ones.
Practice Regularly: Consistent practice can help reduce anxiety by building familiarity and competence.
Seek Support: Talk to teachers, tutors, or classmates about your anxieties.
Use Relaxation Techniques: Practice deep breathing, meditation, or other relaxation techniques to calm your nerves.
Reframe Negative Thoughts: Challenge negative thoughts and replace them with positive affirmations.

LEARNS.EDU.VN offers resources and support to help you overcome math anxiety and build confidence in your abilities.

4.2 Understanding Abstract Concepts

Trigonometry involves several abstract concepts that can be difficult to grasp. Here are some strategies to enhance your understanding:

Visualize Concepts: Use diagrams, graphs, and interactive simulations to visualize abstract concepts.
Relate to Real-World Examples: Connect trigonometric concepts to real-world applications, such as navigation, surveying, and engineering.
Break Down Complex Concepts: Divide complex concepts into smaller, more manageable parts.
Seek Clarification: Don’t hesitate to ask questions and seek clarification from teachers, tutors, or online forums.
Use Analogies and Metaphors: Use analogies and metaphors to relate abstract concepts to more familiar ideas.

LEARNS.EDU.VN provides clear explanations and visual aids to help you understand abstract trigonometric concepts more easily.

4.3 Time Management and Avoiding Procrastination

Effective time management is crucial for learning trigonometry efficiently. Procrastination can lead to stress and hinder your progress. Here are some tips for managing your time and avoiding procrastination:

Create a Study Schedule: Develop a detailed study schedule and stick to it as closely as possible.
Set Realistic Goals: Set achievable goals for each study session to avoid feeling overwhelmed.
Break Down Tasks: Divide large tasks into smaller, more manageable steps.
Prioritize Tasks: Focus on the most important tasks first.
Eliminate Distractions: Create a quiet study environment free from distractions.
Reward Yourself: Reward yourself for completing tasks to stay motivated.

LEARNS.EDU.VN offers tools and resources to help you manage your time effectively and stay on track with your trigonometry studies.

4.4 Knowing When to Seek Help

It’s important to recognize when you need help and to seek assistance from teachers, tutors, or online resources. Don’t struggle in silence if you’re feeling overwhelmed or confused.

Ask Questions: Don’t hesitate to ask questions in class or during tutoring sessions.
Seek Tutoring: Consider hiring a tutor who can provide personalized instruction and support.
Join Study Groups: Collaborate with classmates to review material and solve problems together.
Use Online Forums: Participate in online forums to ask questions and get help from other students and experts.
Consult Textbooks and Resources: Refer to textbooks and online resources for additional explanations and examples.

LEARNS.EDU.VN provides access to expert guidance and support to help you overcome challenges and succeed in your trigonometry journey.

5. Advanced Topics in Trigonometry

Once you’ve mastered the fundamentals of trigonometry, you can explore more advanced topics that build upon these foundational concepts. These topics are essential for further studies in mathematics, physics, engineering, and other fields.

5.1 Trigonometric Equations and Inequalities

Trigonometric equations involve finding the values of angles that satisfy a given equation. Trigonometric inequalities involve finding the range of angles that satisfy a given inequality.

Solving Trigonometric Equations: Use trigonometric identities, algebraic techniques, and inverse trigonometric functions to solve equations.
Solving Trigonometric Inequalities: Use the unit circle and the properties of trigonometric functions to solve inequalities.
General Solutions: Find all possible solutions to trigonometric equations and inequalities.

LEARNS.EDU.VN provides detailed explanations and practice problems to help you master trigonometric equations and inequalities.

5.2 Inverse Trigonometric Functions

Inverse trigonometric functions, also known as arc functions, are the inverse functions of the trigonometric functions. They are used to find the angle that corresponds to a given trigonometric ratio.

Definitions: Understand the definitions of the inverse sine (arcsin), inverse cosine (arccos), and inverse tangent (arctan) functions.
Domain and Range: Know the domain and range of each inverse trigonometric function.
Applications: Apply inverse trigonometric functions to solve problems involving angles and triangles.

LEARNS.EDU.VN offers comprehensive tutorials and examples to help you understand and apply inverse trigonometric functions.

5.3 Applications of Trigonometry in Real-World Scenarios

Trigonometry has numerous applications in various fields, including:

Navigation: Used to determine position and direction.
Surveying: Used to measure distances and angles.
Engineering: Used in structural design, electrical engineering, and mechanical engineering.
Physics: Used to analyze motion, waves, and optics.
Astronomy: Used to measure distances to stars and planets.

LEARNS.EDU.VN provides real-world examples and case studies to illustrate the applications of trigonometry in different fields.

5.4 Trigonometry and Complex Numbers

Trigonometry is closely related to complex numbers. Complex numbers can be represented in polar form using trigonometric functions.

Polar Form of Complex Numbers: Understand how to represent complex numbers in polar form using magnitude and angle.
De Moivre’s Theorem: Apply De Moivre’s theorem to raise complex numbers to powers.
Euler’s Formula: Use Euler’s formula to relate complex exponentials to trigonometric functions.

LEARNS.EDU.VN offers detailed explanations and examples to help you understand the relationship between trigonometry and complex numbers.

6. Resources for Continued Learning and Practice

To continue your trigonometry journey and deepen your understanding, it’s essential to utilize a variety of resources for ongoing learning and practice. These resources can help you stay up-to-date with the latest developments in the field and hone your problem-solving skills.

6.1 Recommended Textbooks and Study Guides

“Trigonometry” by Ted Sundstrom and Steven Schlicker: A comprehensive textbook covering all aspects of trigonometry, from basic concepts to advanced applications.
“Schaum’s Outline of Trigonometry” by Robert E. Moyer and Frank Ayres: A study guide that provides numerous solved problems and practice exercises.
“Trigonometry For Dummies” by Mary Jane Sterling: A user-friendly guide that explains trigonometric concepts in a clear and accessible manner.

6.2 Online Courses and Tutorials

Khan Academy: Offers free video lessons and practice exercises covering a wide range of math topics, including trigonometry.
Coursera and edX: Offer online courses taught by university professors, covering advanced topics in trigonometry and related fields.
LEARNS.EDU.VN: Provides comprehensive articles, tutorials, and practice problems tailored to different skill levels.

6.3 Practice Websites and Mobile Apps

Mathway: A website and mobile app that provides step-by-step solutions to math problems, including trigonometric equations and identities.
Symbolab: A website that offers a variety of math tools, including a trigonometry calculator and a problem solver.
Photomath: A mobile app that allows you to scan math problems and get step-by-step solutions instantly.

6.4 Joining Math Communities and Forums

Math Stack Exchange: A question-and-answer website for math enthusiasts and professionals.
Reddit Math Communities: Subreddits like r/math and r/learnmath offer a platform for discussing math topics and getting help from other users.
Online Math Forums: Websites like Art of Problem Solving offer forums for discussing math problems and sharing solutions.

LEARNS.EDU.VN encourages you to explore these resources and engage with the math community to enhance your learning and stay motivated.

7. Tailoring Your Learning to Specific Goals

The amount of time and effort you dedicate to learning trigonometry may depend on your specific goals and how you plan to use trigonometry in your future endeavors.

7.1 Trigonometry for High School Students

If you’re a high school student, you’ll likely need to learn trigonometry as part of your math curriculum. In this case, you’ll need to:

Focus on Core Concepts: Master the basic trigonometric functions, identities, and equations.
Prepare for Exams: Practice solving problems that are similar to those on your exams.
Seek Help When Needed: Don’t hesitate to ask your teacher or a tutor for help if you’re struggling with the material.
Utilize Online Resources: Use online resources like Khan Academy and LEARNS.EDU.VN to supplement your learning.

7.2 Trigonometry for College Students

If you’re a college student, you may need to learn trigonometry as a prerequisite for calculus, physics, or engineering courses. In this case, you’ll need to:

Master Advanced Topics: Learn about inverse trigonometric functions, complex numbers, and applications of trigonometry in calculus.
Apply Trigonometry to Other Fields: Understand how trigonometry is used in physics, engineering, and other fields.
Practice Problem Solving: Work through a variety of challenging problems to develop your problem-solving skills.
Seek Help from Professors and TAs: Attend office hours and ask questions to clarify any concepts you’re struggling with.

7.3 Trigonometry for Professionals

If you’re a professional in a field that uses trigonometry, you’ll need to:

Focus on Relevant Applications: Learn about the specific applications of trigonometry in your field.
Stay Up-to-Date: Keep up with the latest developments in trigonometry and related fields.
Attend Conferences and Workshops: Attend conferences and workshops to learn from experts and network with other professionals.
Utilize Online Resources: Use online resources like LEARNS.EDU.VN to refresh your knowledge and learn new skills.

8. The Role of Technology in Learning Trigonometry

Technology plays a significant role in modern education, and trigonometry is no exception. Various digital tools and platforms can enhance the learning experience and make complex concepts more accessible.

8.1 Interactive Software and Simulations

Interactive software and simulations can help you visualize trigonometric functions and their properties. These tools allow you to:

Manipulate Angles and Sides: Change the values of angles and sides in a triangle and see how the trigonometric ratios change.
Explore the Unit Circle: Visualize the unit circle and see how the sine, cosine, and tangent functions vary as you move around the circle.
Graph Trigonometric Functions: Graph trigonometric functions and explore their properties, such as amplitude, period, and phase shift.

8.2 Mobile Apps for On-the-Go Learning

Mobile apps can provide convenient access to trigonometric lessons, practice problems, and reference materials. These apps allow you to:

Learn Anytime, Anywhere: Study trigonometry on your smartphone or tablet, whether you’re at home, on the go, or waiting in line.
Practice Problem Solving: Work through a variety of practice problems and get instant feedback.
Access Reference Materials: Look up trigonometric identities, formulas, and definitions quickly and easily.

8.3 Online Calculators and Problem Solvers

Online calculators and problem solvers can help you solve trigonometric equations and simplify expressions. These tools can:

Solve Complex Problems: Solve complex trigonometric problems that would be difficult or time-consuming to solve by hand.
Check Your Work: Check your work and make sure you’re on the right track.
Explore Different Solutions: Explore different approaches to solving trigonometric problems.

LEARNS.EDU.VN provides links to a variety of online tools and resources to help you learn trigonometry more effectively.

9. Maintaining Motivation and Staying Consistent

Learning trigonometry can be challenging, and it’s important to maintain motivation and stay consistent with your studies.

9.1 Setting Achievable Goals

Set achievable goals for each study session to avoid feeling overwhelmed. Break down large tasks into smaller, more manageable steps.

9.2 Tracking Progress and Celebrating Successes

Track your progress and celebrate your successes to stay motivated. Use a study journal or a mobile app to record your accomplishments and identify areas where you need more practice.

9.3 Finding a Study Buddy or Joining a Study Group

Find a study buddy or join a study group to stay accountable and get support from other learners. Working with others can make learning more enjoyable and help you stay motivated.

9.4 Rewarding Yourself for Milestones

Reward yourself for reaching milestones to stay motivated. Treat yourself to something you enjoy after completing a challenging chapter or acing an exam.

LEARNS.EDU.VN encourages you to stay positive, persistent, and focused on your goals throughout your trigonometry journey.

10. Frequently Asked Questions (FAQs) About Learning Trigonometry

Here are some frequently asked questions about learning trigonometry:

How long does it take to learn basic trigonometry?
- Learning basic trigonometry typically takes between 20 to 40 hours of study and practice.
Is trigonometry difficult to learn?
- Trigonometry can be challenging, especially if you have gaps in your math foundation. However, with consistent effort and the right resources, it’s definitely achievable.
What are the prerequisites for learning trigonometry?
- The prerequisites for learning trigonometry include a solid understanding of algebra and geometry.
What are the best resources for learning trigonometry online?
- Some of the best online resources for learning trigonometry include Khan Academy, LEARNS.EDU.VN, and Wolfram Alpha.
How can I memorize trigonometric identities?
- You can memorize trigonometric identities by using repetition, mnemonics, flashcards, and derivation.
How can I overcome math anxiety?
- You can overcome math anxiety by identifying the source, building confidence, practicing regularly, and seeking support.
What are some real-world applications of trigonometry?
- Trigonometry has numerous applications in navigation, surveying, engineering, physics, and astronomy.
How can I use technology to learn trigonometry?
- You can use technology to learn trigonometry by utilizing interactive software, mobile apps, and online calculators.
How can I stay motivated while learning trigonometry?
- You can stay motivated while learning trigonometry by setting achievable goals, tracking progress, finding a study buddy, and rewarding yourself for milestones.
Where can I find expert guidance and support for learning trigonometry?
- You can find expert guidance and support for learning trigonometry at LEARNS.EDU.VN, which offers comprehensive articles, tutorials, and access to knowledgeable educators.

By understanding the fundamentals, utilizing effective learning strategies, and maintaining a positive attitude, you can successfully master trigonometry and unlock its many applications. Remember, the journey of learning is a marathon, not a sprint. Consistency, patience, and the right resources are your best allies. And for comprehensive support and expert guidance, visit LEARNS.EDU.VN today.

Are you struggling with trigonometry and looking for more in-depth explanations, practice problems, and personalized guidance? Visit learns.edu.vn today to discover a wealth of resources designed to help you master trigonometry and excel in your studies. Contact us at 123 Education Way, Learnville, CA 90210, United States or Whatsapp: +1 555-555-1212. Let us help you unlock your full potential.