Learning how to calculate square roots can seem daunting, but it’s a fundamental skill with applications across various fields. At LEARNS.EDU.VN, we believe everyone can master this concept with the right guidance. This comprehensive guide will break down the process of How To Learn Square Root, exploring various methods, providing clear examples, and equipping you with the knowledge to confidently tackle square root problems. Discover effective techniques for calculating square roots, understand the square root definition, and master root extraction with ease.
Here’s what we’ll cover:
- Understanding the square root concept.
- Different methods to calculate square roots.
- Simplifying square roots.
- Applications of square roots.
- And much more!
1. Understanding Square Roots: The Basics
The square root of a number ‘x’ is a value ‘y’ that, when multiplied by itself, equals ‘x’. In mathematical terms, if y y = x, then ‘y’ is the square root of ‘x’. This concept is fundamental in algebra, geometry, and various scientific calculations. According to a study by the National Mathematics Advisory Panel, understanding square roots is crucial for students to progress in advanced mathematics (Source: Foundations for Success: The Final Report of the National Mathematics Advisory Panel*, 2008).
1.1. Definition of Square Root
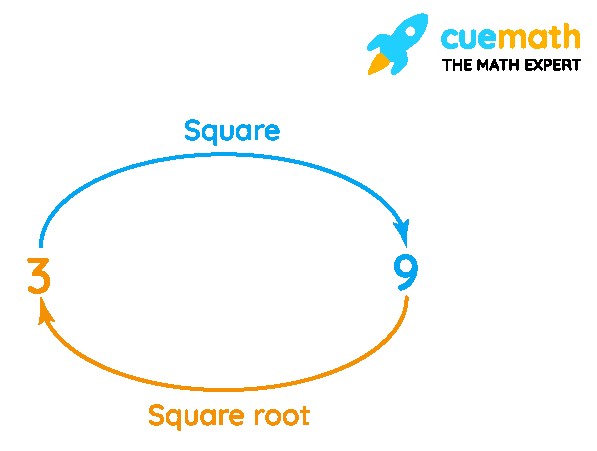
The square root definition is simple: it’s a number that, when squared (multiplied by itself), gives you the original number. For example, the square root of 9 is 3 because 3 * 3 = 9. We can also say that root extraction is the process of finding the square root of a number.
1.2. Symbol and Notation
The symbol used to denote the square root is √, also known as the radical symbol. The number under the radical symbol is called the radicand. For instance, in √25, the symbol √ represents the square root operation, and 25 is the radicand. The expression √25 asks, “What number, when multiplied by itself, equals 25?” The answer, of course, is 5.
1.3. Perfect Squares vs. Non-Perfect Squares
- Perfect Squares: These are numbers that are the result of squaring an integer (a whole number). Examples include 4 (2 2), 9 (3 3), 16 (4 4), 25 (5 5), and so on.
- Non-Perfect Squares: These are numbers whose square roots are not integers. For instance, the square root of 2 is approximately 1.414, which is not an integer. Similarly, the square root of 7 is approximately 2.646, which is also not an integer.
Recognizing perfect squares can greatly simplify the process of calculating square roots, as their square roots are whole numbers.
1.4. Why Learn About Square Roots?
Understanding square roots is essential for several reasons:
- Algebra: Square roots are fundamental in solving algebraic equations and simplifying expressions.
- Geometry: They are used to find lengths and distances in geometric problems, such as calculating the length of a diagonal in a square.
- Science and Engineering: Square roots are used in various scientific and engineering calculations, including physics, chemistry, and computer science.
- Everyday Life: They can be applied in practical situations like calculating areas and volumes, understanding financial rates, and more.
2. Different Methods to Learn How To Calculate Square Root
There are several methods to learn how to calculate square root, each with its own advantages and suitability for different situations. Let’s explore some of the most common methods:
2.1. Prime Factorization Method
The prime factorization method involves breaking down a number into its prime factors and then pairing those factors to find the square root. This method is particularly effective for perfect squares.
Steps:
- Prime Factorization: Break down the number into its prime factors.
- Pairing Factors: Group the prime factors into pairs of identical factors.
- Extracting Pairs: Take one factor from each pair.
- Multiplying Factors: Multiply the extracted factors together to get the square root.
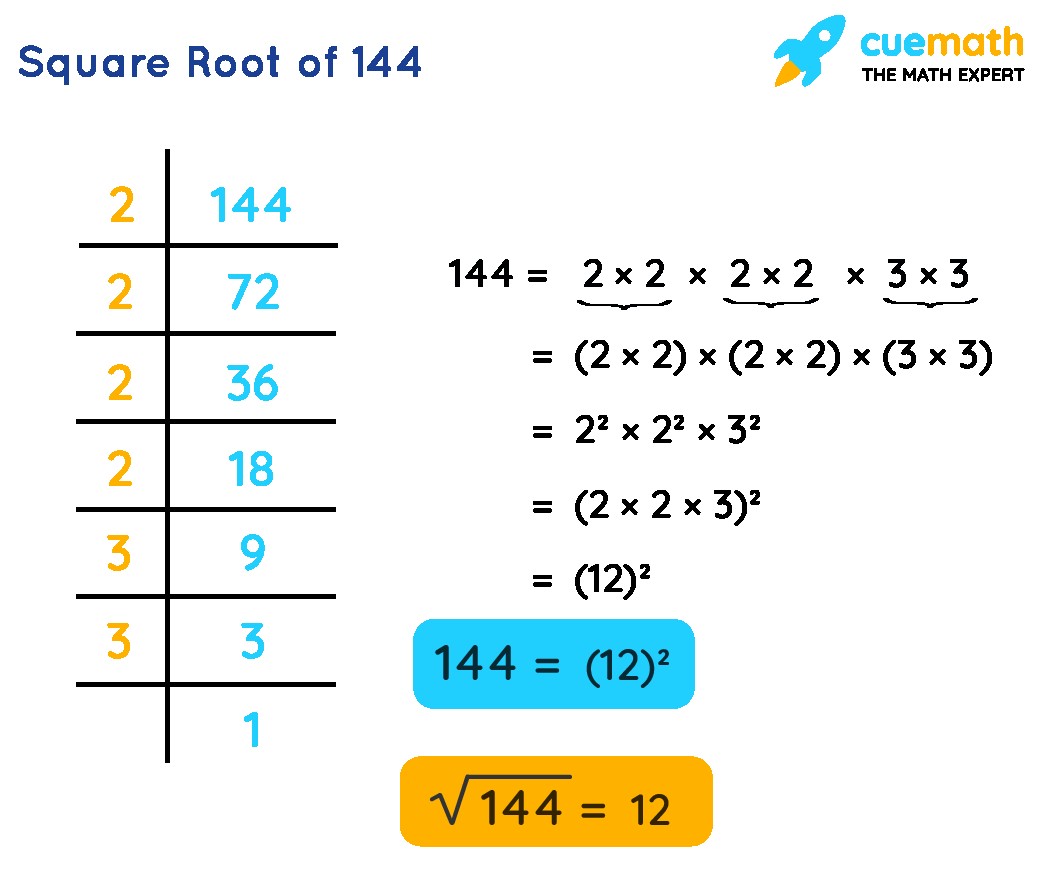
Example: Find the square root of 144.
- Prime Factorization: 144 = 2 x 2 x 2 x 2 x 3 x 3
- Pairing Factors: (2 x 2) x (2 x 2) x (3 x 3)
- Extracting Pairs: 2 x 2 x 3
- Multiplying Factors: 2 x 2 x 3 = 12
Therefore, the square root of 144 is 12.
2.2. Estimation Method
The estimation method is useful for approximating the square root of a number when you don’t need an exact answer. It involves finding the nearest perfect squares and narrowing down the estimate.
Steps:
- Identify Nearest Perfect Squares: Find the perfect squares that are closest to the given number.
- Determine Range: The square root of the given number will lie between the square roots of the nearest perfect squares.
- Estimate: Make an educated guess based on how close the number is to each perfect square.
- Refine: Refine your estimate by squaring it and adjusting as necessary.
Example: Estimate the square root of 28.
- Identify Nearest Perfect Squares: 25 and 36 are the nearest perfect squares to 28.
- Determine Range: √25 = 5 and √36 = 6, so √28 lies between 5 and 6.
- Estimate: Since 28 is closer to 25 than 36, estimate √28 to be around 5.3.
- Refine: 5.3 * 5.3 = 28.09, which is close to 28.
Therefore, the square root of 28 is approximately 5.3.
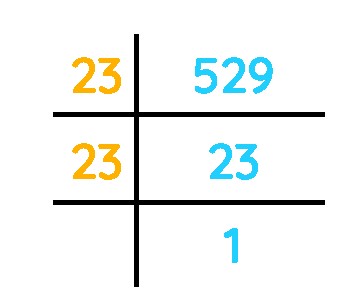
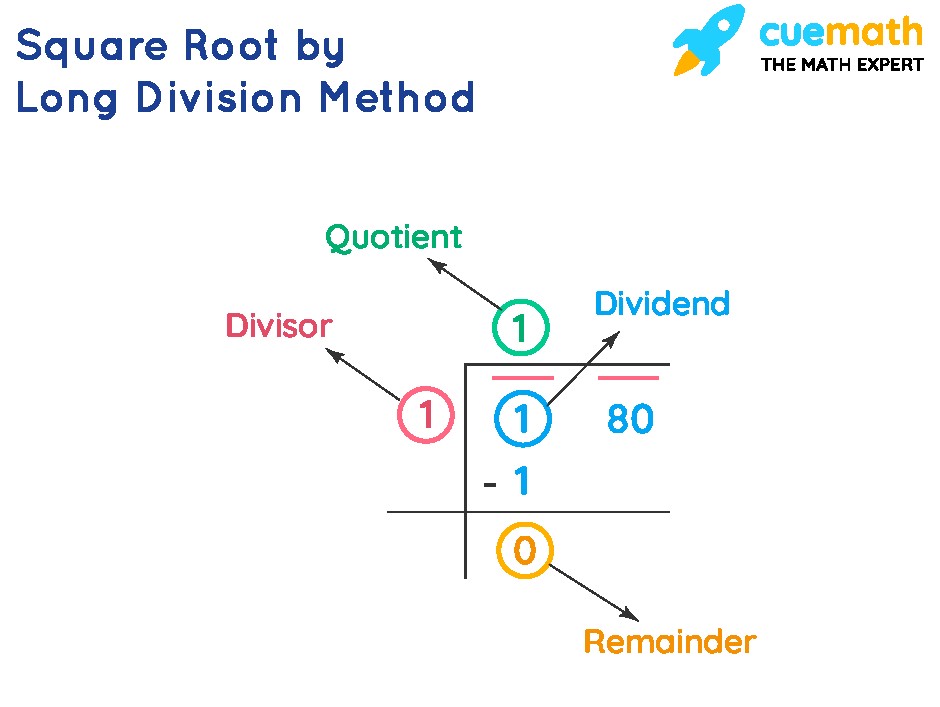
2.3. Long Division Method
The long division method is a systematic way to find the square root of any number, whether it is a perfect square or not. This method is particularly useful when dealing with larger numbers or non-perfect squares.
Steps:
- Grouping Digits: Start by grouping the digits of the number in pairs, starting from the right.
- Finding the Largest Divisor: Find the largest integer whose square is less than or equal to the leftmost group.
- Divisor and Quotient: Use this integer as both the divisor and the quotient for the first step.
- Subtract and Bring Down: Subtract the square of the divisor from the first group and bring down the next pair of digits.
- New Divisor: Form a new divisor by doubling the quotient and appending a digit such that the new divisor multiplied by this digit is less than or equal to the new dividend.
- Repeat: Repeat steps 4 and 5 until you reach the desired level of accuracy.
Example: Find the square root of 54756.
- Grouping Digits: 5 47 56 (grouping pairs from right to left)
- Finding the Largest Divisor: The largest integer whose square is less than or equal to 5 is 2.
- Divisor and Quotient: Divisor = 2, Quotient = 2
- Subtract and Bring Down: 5 – (2 * 2) = 1, Bring down 47 to get 147
- New Divisor: Double the quotient (2 2 = 4) and find a digit to append such that 4x x <= 147. The digit is 3, so the new divisor is 43.
- Repeat: 147 – (43 3) = 18, Bring down 56 to get 1856. Double the current quotient (23 2 = 46) and find a digit to append such that 46x x <= 1856. The digit is 4, so the new divisor is 464. 1856 – (464 4) = 0.
Therefore, the square root of 54756 is 234.
2.4. Repeated Subtraction Method
The repeated subtraction method is a simple way to find the square root of perfect squares. This method involves repeatedly subtracting consecutive odd numbers from the original number until you reach zero. The number of subtractions needed is the square root of the original number.
Steps:
- Start Subtracting: Begin by subtracting the first odd number (1) from the given number.
- Continue Subtracting: Continue subtracting consecutive odd numbers (3, 5, 7, etc.) from the result of each previous subtraction.
- Reach Zero: Repeat the process until you reach zero.
- Count Subtractions: Count the number of subtractions performed. This number is the square root of the original number.
Example: Find the square root of 16 using the repeated subtraction method.
- 16 – 1 = 15
- 15 – 3 = 12
- 12 – 5 = 7
- 7 – 7 = 0
Since it took 4 subtractions to reach zero, the square root of 16 is 4.
2.5. Newton-Raphson Method
The Newton-Raphson method is an iterative method used to find successively better approximations to the roots (or zeroes) of a real-valued function. In the context of finding square roots, it involves iteratively refining an initial guess until it converges to the actual square root.
Steps:
- Make an Initial Guess: Start with an initial guess for the square root of the number.
- Iterate: Use the formula: nextGuess = 0.5 (previousGuess + (number / previousGuess*)).
- Refine: Repeat step 2 until the nextGuess is sufficiently close to the previousGuess.
Example: Find the square root of 25 using the Newton-Raphson method.
- Make an Initial Guess: Let’s start with an initial guess of 4.
- Iterate:
- nextGuess = 0.5 (4 + (25 / 4)) = 0.5 (4 + 6.25) = 5.125
- nextGuess = 0.5 (5.125 + (25 / 5.125)) = 0.5 (5.125 + 4.878) = 5.0015
- nextGuess = 0.5 (5.0015 + (25 / 5.0015)) = 0.5 (5.0015 + 4.9985) = 5.0000
- Refine: After a few iterations, the guess converges to 5.
Therefore, the square root of 25 is 5.
3. Simplifying Square Roots: A Step-by-Step Guide
Simplifying square roots involves reducing them to their simplest form. This is particularly useful when dealing with non-perfect squares, as it allows you to express them as a product of an integer and a simplified radical. This skill is essential for learning how to calculate square root efficiently.
3.1. Identifying Perfect Square Factors
The first step in simplifying square roots is to identify any perfect square factors of the radicand (the number under the square root symbol).
Steps:
- List Factors: List the factors of the radicand.
- Identify Perfect Squares: Identify any factors that are perfect squares (1, 4, 9, 16, 25, etc.).
- Choose Largest Perfect Square: Choose the largest perfect square factor.
Example: Simplify √72.
- List Factors: The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
- Identify Perfect Squares: The perfect square factors are 1, 4, 9, and 36.
- Choose Largest Perfect Square: The largest perfect square factor is 36.
3.2. Factoring Out Perfect Squares
Once you’ve identified the largest perfect square factor, you can factor it out of the radicand.
Steps:
- Rewrite Radicand: Rewrite the radicand as the product of the perfect square factor and the remaining factor.
- Separate Radicals: Use the property √(a b) = √a √b to separate the radicals.
- Simplify Perfect Square: Simplify the square root of the perfect square factor.
Example: Simplify √72.
- Rewrite Radicand: √72 = √(36 * 2)
- Separate Radicals: √(36 2) = √36 √2
- Simplify Perfect Square: √36 * √2 = 6√2
Therefore, √72 simplified is 6√2.
3.3. Examples of Simplifying Square Roots
Let’s go through a few more examples to illustrate the process of simplifying square roots.
-
Example 1: Simplify √48.
- Largest perfect square factor: 16
- Rewrite: √48 = √(16 * 3)
- Separate: √16 * √3
- Simplify: 4√3
-
Example 2: Simplify √125.
- Largest perfect square factor: 25
- Rewrite: √125 = √(25 * 5)
- Separate: √25 * √5
- Simplify: 5√5
-
Example 3: Simplify √98.
- Largest perfect square factor: 49
- Rewrite: √98 = √(49 * 2)
- Separate: √49 * √2
- Simplify: 7√2
3.4. Simplifying Square Roots with Variables
The same principles apply when simplifying square roots that contain variables. The key is to look for even exponents, as they indicate perfect squares.
Example: Simplify √(x^3).
- Rewrite: √(x^3) = √(x^2 * x)
- Separate: √(x^2 x) = √(x^2) √x
- Simplify: x√x
Example: Simplify √(16y^5).
- Rewrite: √(16y^5) = √(16 y^4 y)
- Separate: √(16 y^4 y) = √16 √(y^4) √y
- Simplify: 4y^2√y
3.5. Additional Tips for Simplifying Square Roots
- Always look for the largest perfect square factor to simplify in one step.
- If you’re unsure, start by factoring the number into its prime factors.
- Remember, you can only simplify square roots of positive numbers.
4. Real-World Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous practical applications in various fields. Understanding these applications can help you appreciate the importance of learning how to calculate square root.
4.1. Geometry
In geometry, square roots are commonly used to calculate lengths, distances, and areas.
- Pythagorean Theorem: The Pythagorean theorem, a^2 + b^2 = c^2, involves finding the square root of the sum of the squares of two sides of a right triangle to find the length of the hypotenuse.
- Area of a Circle: The area of a circle is given by A = πr^2, where ‘r’ is the radius. To find the radius if you know the area, you would use the square root: r = √(A/π).
- Distance Formula: The distance between two points (x1, y1) and (x2, y2) in a coordinate plane is given by d = √((x2 – x1)^2 + (y2 – y1)^2).
4.2. Physics
Square roots appear frequently in physics equations and calculations.
- Kinetic Energy: The kinetic energy (KE) of an object is given by KE = 0.5 m v^2, where ‘m’ is the mass and ‘v’ is the velocity. To find the velocity if you know the kinetic energy, you would use the square root: v = √(2 * KE / m).
- Period of a Pendulum: The period (T) of a simple pendulum is given by T = 2π√(L/g), where ‘L’ is the length of the pendulum and ‘g’ is the acceleration due to gravity.
- Root Mean Square (RMS) Velocity: In thermodynamics, the RMS velocity of gas molecules is calculated using square roots.
4.3. Engineering
Engineers use square roots in various calculations, from structural design to signal processing.
- Structural Design: Square roots are used to calculate stress, strain, and other parameters in structural analysis.
- Electrical Engineering: In electrical engineering, square roots are used to calculate RMS values of alternating current (AC) and voltage.
- Signal Processing: Square roots are used in signal processing algorithms, such as calculating the magnitude of a complex signal.
4.4. Computer Science
Square roots are used in computer graphics, game development, and various algorithms.
- 3D Graphics: In 3D graphics, square roots are used to calculate distances, normalize vectors, and perform other geometric calculations.
- Game Development: Square roots are used in game physics, collision detection, and other game-related calculations.
- Cryptography: Square roots are used in some cryptographic algorithms.
4.5. Finance
In finance, square roots are used to calculate standard deviations and other statistical measures.
- Standard Deviation: The standard deviation (σ) of a dataset is a measure of the amount of variation or dispersion of a set of values. It involves calculating the square root of the variance.
- Portfolio Management: Square roots are used in portfolio management to calculate risk metrics and optimize investment strategies.
4.6. Surveying
Surveyors use square roots to calculate distances, areas, and elevations.
- Area Calculation: Square roots are used to calculate the area of land parcels and other geometric shapes.
- Elevation Calculation: Square roots are used in leveling and other surveying techniques.
5. Advanced Topics: Square Roots of Negative Numbers and Complex Numbers
While we typically deal with square roots of positive numbers, it’s important to understand what happens when we encounter square roots of negative numbers. This leads us to the realm of complex numbers.
5.1. Imaginary Unit “i”
The imaginary unit, denoted by “i,” is defined as the square root of -1. That is, i = √(-1). This concept is fundamental to understanding square roots of negative numbers.
5.2. Square Roots of Negative Numbers
To find the square root of a negative number, we express it as a product of i and the square root of the corresponding positive number.
Example: Find the square root of -25.
- Rewrite: √(-25) = √(25 * -1)
- Separate: √(25 -1) = √25 √(-1)
- Simplify: √25 * √(-1) = 5i
Therefore, the square root of -25 is 5i.
5.3. Complex Numbers
A complex number is a number that can be expressed in the form a + bi, where “a” and “b” are real numbers, and “i” is the imaginary unit. In this form, “a” is the real part, and “bi” is the imaginary part.
Example: 3 + 4i is a complex number, where 3 is the real part, and 4i is the imaginary part.
5.4. Operations with Complex Numbers
Complex numbers can be added, subtracted, multiplied, and divided using specific rules.
- Addition: (a + bi) + (c + di) = (a + c) + (b + d)i
- Subtraction: (a + bi) – (c + di) = (a – c) + (b – d)i
- Multiplication: (a + bi) * (c + di) = (ac – bd) + (ad + bc)i
- Division: Division is more complex and involves multiplying the numerator and denominator by the conjugate of the denominator.
5.5. Applications of Complex Numbers
Complex numbers have numerous applications in various fields.
- Electrical Engineering: Complex numbers are used to analyze alternating current (AC) circuits.
- Quantum Mechanics: Complex numbers are used in quantum mechanics to describe wave functions.
- Fluid Dynamics: Complex numbers are used to analyze fluid flow.
6. Tips and Tricks for Mastering Square Roots
Mastering square roots requires practice and a solid understanding of the underlying concepts. Here are some tips and tricks to help you improve your skills:
6.1. Memorize Perfect Squares
Memorizing the squares of numbers from 1 to 20 can greatly speed up your calculations and estimations.
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
| 20 | 400 |
6.2. Practice Regularly
Regular practice is key to mastering any mathematical concept. Set aside some time each day to work on square root problems.
6.3. Use Flashcards
Create flashcards with square root problems on one side and the answers on the other. This can help you memorize perfect squares and practice your skills.
6.4. Utilize Online Resources
There are many online resources available to help you learn and practice square roots. Websites like Khan Academy, Cuemath, and others offer lessons, practice problems, and quizzes.
6.5. Break Down Complex Problems
When faced with a complex square root problem, break it down into smaller, more manageable steps.
6.6. Understand the Concepts
Focus on understanding the underlying concepts rather than just memorizing formulas and procedures. This will help you apply your knowledge to a wider range of problems.
6.7. Seek Help When Needed
Don’t be afraid to ask for help from teachers, tutors, or classmates if you’re struggling with square roots.
7. Common Mistakes to Avoid When Calculating Square Roots
Calculating square roots can be tricky, and it’s easy to make mistakes if you’re not careful. Here are some common mistakes to avoid:
7.1. Forgetting the Plus/Minus Sign
Remember that every positive number has two square roots: one positive and one negative. For example, the square root of 9 is both 3 and -3.
7.2. Incorrectly Simplifying Square Roots
Make sure to identify the largest perfect square factor when simplifying square roots. Otherwise, you may not simplify the radical completely.
7.3. Confusing Square Roots with Squares
Don’t confuse the square root of a number with the square of a number. The square root of 9 is 3, while the square of 3 is 9.
7.4. Making Arithmetic Errors
Arithmetic errors can easily occur when performing long division or other calculations. Double-check your work to avoid mistakes.
7.5. Ignoring the Order of Operations
Follow the order of operations (PEMDAS/BODMAS) when calculating square roots in complex expressions.
7.6. Assuming All Numbers Have Integer Square Roots
Not all numbers have integer square roots. Many numbers have square roots that are irrational numbers.
8. Frequently Asked Questions (FAQs) About Square Roots
1. What is a square root?
A square root of a number ‘x’ is a value ‘y’ that, when multiplied by itself, equals ‘x’. In other words, if y * y = x, then ‘y’ is the square root of ‘x’.
2. How do I calculate the square root of a number?
There are several methods for calculating square roots, including the prime factorization method, estimation method, long division method, and Newton-Raphson method.
3. Can a square root be negative?
Yes, every positive number has two square roots: one positive and one negative. For example, the square root of 9 is both 3 and -3.
4. What is the square root of a negative number?
The square root of a negative number is an imaginary number. It is expressed as a multiple of the imaginary unit “i,” where i = √(-1).
5. How do I simplify a square root?
To simplify a square root, find the largest perfect square factor of the radicand and factor it out of the radical. For example, √72 = √(36 2) = √36 √2 = 6√2.
6. What are the real-world applications of square roots?
Square roots have numerous practical applications in various fields, including geometry, physics, engineering, computer science, and finance.
7. How do I find the square root of a decimal number?
You can find the square root of a decimal number using the long division method or a calculator.
8. What is the difference between a square root and a square?
The square root of a number is a value that, when multiplied by itself, equals the original number. The square of a number is the result of multiplying the number by itself. For example, the square root of 9 is 3, while the square of 3 is 9.
9. How do I use a calculator to find the square root of a number?
To find the square root of a number using a calculator, simply enter the number and press the square root button (√).
10. What is the formula for calculating the square root of a number?
The square root of a number ‘x’ can be expressed as x^(1/2) or √x.
9. Level Up Your Learning with LEARNS.EDU.VN
At LEARNS.EDU.VN, we understand that learning new concepts can sometimes be challenging. That’s why we’re committed to providing you with the resources and support you need to succeed. Whether you’re struggling with root extraction, need help calculating square roots, or simply want to deepen your understanding of the square root definition, we’ve got you covered.
9.1. Comprehensive Learning Materials
Our website offers a wide range of learning materials, including articles, tutorials, videos, and practice problems. These resources are designed to help you learn at your own pace and master the skills you need to succeed.
9.2. Expert Instructors
Our team of expert instructors is dedicated to providing you with the highest quality education. They are passionate about teaching and committed to helping you achieve your goals.
9.3. Personalized Learning
We understand that everyone learns differently. That’s why we offer personalized learning experiences tailored to your individual needs and learning style.
9.4. Interactive Learning Tools
Our interactive learning tools make learning fun and engaging. These tools include quizzes, games, and simulations that help you practice your skills and reinforce your understanding.
9.5. Community Support
Join our community of learners to connect with other students, share your knowledge, and get support from your peers.
9.6. Track Your Progress
Monitor your progress and see how you’re improving over time. Our tracking tools allow you to see your strengths and weaknesses so you can focus your efforts on the areas where you need the most help.
9.7. Learn Anytime, Anywhere
With LEARNS.EDU.VN, you can learn anytime, anywhere. Our website is accessible on any device, so you can study whenever and wherever it’s convenient for you.
Conclusion
Learning how to calculate square roots is a valuable skill that can be applied in many areas of life. By understanding the basic concepts, mastering the different methods, and practicing regularly, you can become proficient in calculating square roots and unlock new opportunities in your academic and professional pursuits. Remember, LEARNS.EDU.VN is here to support you every step of the way.
Ready to take your learning to the next level? Visit LEARNS.EDU.VN today to discover a world of knowledge and unlock your full potential. Whether you’re looking for in-depth articles, engaging video tutorials, or personalized learning support, we have everything you need to succeed. Don’t wait, start your journey to success with LEARNS.EDU.VN now!
Contact us:
- Address: 123 Education Way, Learnville, CA 90210, United States
- WhatsApp: +1 555-555-1212
- Website: learns.edu.vn