Are you looking to understand How To Learn Square Roots effectively? At LEARNS.EDU.VN, we provide a comprehensive guide that simplifies the concept of square roots, making it accessible for learners of all ages and backgrounds. Whether you are a student aiming to ace your exams, a professional looking to brush up on your math skills, or simply someone curious about mathematics, our step-by-step instructions and practical examples will help you master the art of finding square roots. Discover the joy of problem-solving and enhance your mathematical prowess with our expert-curated content. Explore techniques like prime factorization, long division, and estimation to confidently solve square root problems.
1. Understanding the Essence of Square Roots
The square root of a number is a value that, when multiplied by itself, equals the original number. Essentially, it’s the inverse operation of squaring a number. Imagine you have a square, and you know its area. The square root helps you find the length of one of its sides.
1.1. Defining the Square Root
Formally, if ‘a’ is the square root of ‘b’, then a × a = b. Every positive number has two square roots: a positive value and a negative value. For instance, both 3 and -3 are square roots of 9 because 33 = 9 and (-3)(-3) = 9. However, the principal square root is usually the positive value.
1.2. The Significance of Square Roots in Mathematics
Square roots are fundamental in various mathematical fields:
- Geometry: Calculating lengths and distances.
- Algebra: Solving equations.
- Calculus: Analyzing functions and their properties.
- Physics: Determining physical quantities like velocity and acceleration.
- Computer Science: Implementing algorithms for graphics and data analysis.
Understanding square roots opens doors to advanced mathematical concepts and practical applications.
2. Practical Methods on How to Find Square Roots
There are several methods to find square roots, each with its own advantages. Here’s a detailed look at some of the most common techniques.
2.1. Prime Factorization Method
Prime factorization involves breaking down a number into its prime factors. This method is particularly useful for perfect squares.
Steps:
- Find the Prime Factors: Break down the number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11).
- Pair the Factors: Group the prime factors into pairs of identical factors.
- Extract One from Each Pair: Take one factor from each pair.
- Multiply the Extracted Factors: Multiply the extracted factors to get the square root.
Example:
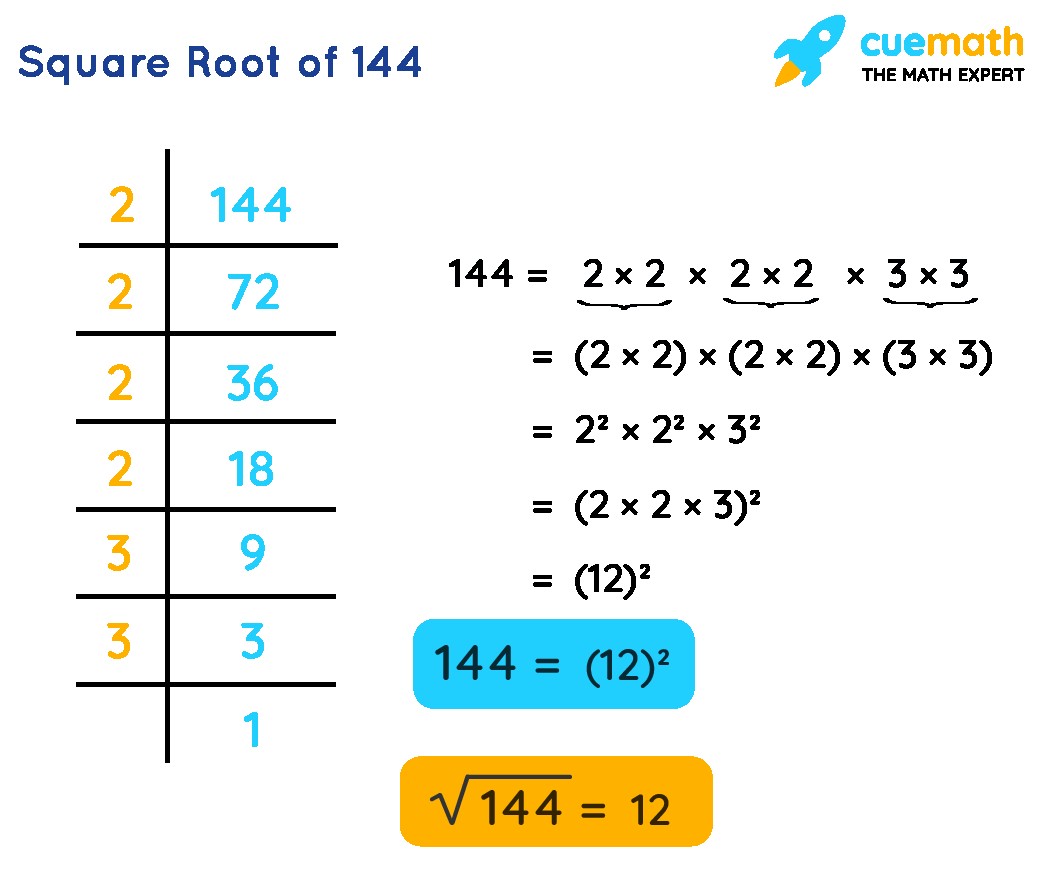
Find the square root of 144.
- Prime factors of 144: 2 × 2 × 2 × 2 × 3 × 3
- Pairing: (2 × 2) × (2 × 2) × (3 × 3)
- Extract: 2 × 2 × 3
- Multiply: 2 × 2 × 3 = 12
Therefore, √144 = 12.
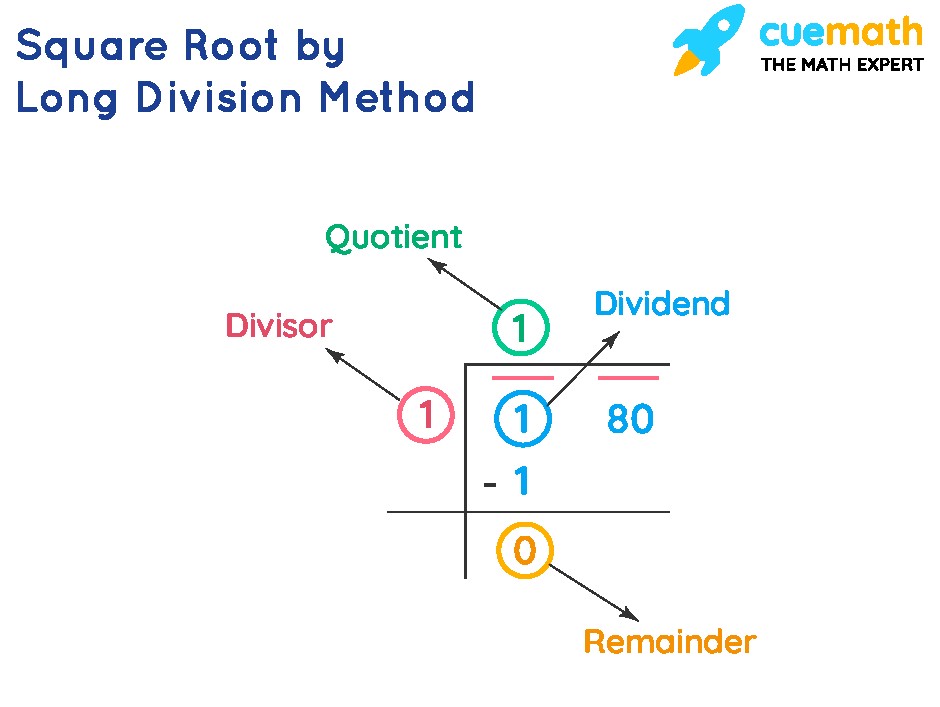
2.2. Long Division Method
The long division method is a versatile technique that works for both perfect and non-perfect squares. It involves a step-by-step division process to approximate the square root.
Steps:
- Group the Digits: Start from the right, group the digits of the number into pairs. If there’s an odd number of digits, the leftmost single digit is also a group.
- Find the Largest Square: Find the largest number whose square is less than or equal to the leftmost group.
- Divide and Subtract: Use this number as the divisor and the quotient for the first division. Subtract the square of the quotient from the leftmost group.
- Bring Down the Next Pair: Bring down the next pair of digits to the right of the remainder.
- Create the New Divisor: Double the current quotient and write it to the left of the new dividend (the remainder combined with the next pair of digits).
- Find the Next Digit: Find a digit to place next to the doubled quotient so that the new number, when multiplied by this digit, is less than or equal to the new dividend.
- Repeat: Repeat steps 4-6 until you reach the desired level of accuracy or have processed all pairs of digits.
Example:
Find the square root of 625.
- Grouping: 6 25
- Largest Square: The largest square less than or equal to 6 is 4 (2*2). So, the first digit of the square root is 2.
- Divide and Subtract:
- Divisor = 2, Quotient = 2
- 6 – (2*2) = 2
- Bring Down: Bring down 25. The new dividend is 225.
- New Divisor: Double the quotient (2*2 = 4). Write 4 to the left of 225.
- Find Next Digit: Find a digit to place next to 4 (let’s call it x) such that (4x)x is less than or equal to 225. Try 5: (45)5 = 225.
- Repeat: Since (45)*5 = 225 exactly, the remainder is 0, and the square root is 25.
Therefore, √625 = 25.
2.3. Estimation Method
The estimation method is useful for quickly approximating the square root of a number without precise calculations.
Steps:
- Identify Nearest Perfect Squares: Find the nearest perfect square numbers above and below the given number.
- Determine the Range: The square root of the given number will lie between the square roots of these two perfect squares.
- Estimate: Based on the proximity to the perfect squares, estimate where the square root lies within the range.
- Refine: Refine your estimate by testing numbers within the range until you get a satisfactory approximation.
Example:
Estimate the square root of 75.
- Nearest Perfect Squares: 64 (√64 = 8) and 81 (√81 = 9)
- Determine the Range: √75 lies between 8 and 9.
- Estimate: 75 is closer to 81 than 64, so √75 will be closer to 9.
- Refine:
- Try 8.5: 8.5 * 8.5 = 72.25 (Too low)
- Try 8.6: 8.6 * 8.6 = 73.96 (Closer)
- Try 8.7: 8.7 * 8.7 = 75.69 (Slightly high)
Therefore, √75 ≈ 8.66.
2.4. Repeated Subtraction Method
This method involves subtracting consecutive odd numbers from the given number until you reach zero. The number of steps it takes to reach zero is the square root.
Steps:
- Subtract Consecutive Odd Numbers: Start subtracting consecutive odd numbers (1, 3, 5, 7, …) from the number.
- Count the Steps: The number of subtractions needed to reach zero is the square root of the number.
Example:
Find the square root of 16 using the repeated subtraction method.
- 16 – 1 = 15
- 15 – 3 = 12
- 12 – 5 = 7
- 7 – 7 = 0
It took 4 steps to reach zero, so √16 = 4.
This method is best suited for perfect squares and smaller numbers.
3. The Square Root Table: A Quick Reference
A square root table provides a quick reference for the square roots of various numbers. It’s a handy tool for students and professionals alike.
3.1. Constructing a Square Root Table
You can create a square root table by listing numbers and their corresponding square roots. Here’s a small example:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
3.2. Using the Square Root Table
To use the table, simply find the number in the first column, and the corresponding value in the second column is its square root. For example, to find the square root of 5, look up 5 in the table, and you’ll find that √5 ≈ 2.236.
4. Formulas and Properties of Square Roots
Understanding the formulas and properties of square roots can simplify complex calculations and problem-solving.
4.1. Basic Square Root Formula
The fundamental formula for a square root is:
√x = x1/2
This means the square root of x is equivalent to x raised to the power of 1/2.
4.2. Properties of Square Roots
- Product Property: √(a b) = √a √b
- Quotient Property: √(a / b) = √a / √b
- Square Root of a Square: √(a2) = |a| (absolute value of a)
4.3. Examples Using Formulas and Properties
- Product Property:
- √(4 9) = √4 √9
- √36 = 2 * 3
- 6 = 6
- Quotient Property:
- √(16 / 4) = √16 / √4
- √4 = 4 / 2
- 2 = 2
- Square Root of a Square:
- √(52) = |5|
- √25 = 5
5. Simplifying Square Roots
Simplifying square roots involves expressing them in their simplest form. This often means removing perfect square factors from under the radical.
5.1. Steps to Simplify Square Roots
- Find Prime Factors: Determine the prime factors of the number under the square root.
- Identify Pairs: Look for pairs of identical prime factors.
- Extract Pairs: For each pair, take one factor out of the square root.
- Multiply: Multiply the factors extracted from the square root and leave any unpaired factors under the square root.
5.2. Examples of Simplifying Square Roots
- Simplify √50:
- Prime factors of 50: 2 × 5 × 5
- Pair: (5 × 5)
- Extract: 5
- Simplified form: 5√2
- Simplify √72:
- Prime factors of 72: 2 × 2 × 2 × 3 × 3
- Pairs: (2 × 2) × (3 × 3)
- Extract: 2 × 3
- Simplified form: 6√2
6. Dealing with Square Roots of Negative Numbers
The square root of a negative number is not a real number but an imaginary number. This concept is crucial in complex number theory.
6.1. Introduction to Imaginary Numbers
An imaginary number is a multiple of the imaginary unit “i”, where i is defined as √(-1).
6.2. Expressing Square Roots of Negative Numbers
To express the square root of a negative number, use the formula:
√(-x) = i√x
Where x is a positive number and i is the imaginary unit.
6.3. Examples with Negative Numbers
- √(-16) = i√16 = 4i
- √(-25) = i√25 = 5i
- √(-7) = i√7
7. Squaring Numbers: The Reverse Operation
Squaring a number is the inverse operation of finding its square root. It involves multiplying a number by itself.
7.1. Definition of Squaring a Number
The square of a number ‘y’ is y * y, often written as y².
7.2. Examples of Squaring Numbers
- 5² = 5 * 5 = 25
- 10² = 10 * 10 = 100
- (3.2)² = 3.2 * 3.2 = 10.24
- (-4)² = -4 * -4 = 16
7.3. Relationship Between Squaring and Square Roots
If x² = y, then √y = x. Squaring and finding the square root are inverse operations. This relationship is fundamental in solving algebraic equations and understanding mathematical concepts.
8. Squares and Square Roots: A Comparative Analysis
Squares and square roots are closely related yet distinct concepts. Understanding their differences is essential for mathematical proficiency.
8.1. Key Differences
| Feature | Square | Square Root |
|---|---|---|
| Definition | Number multiplied by itself | Number that produces the given number when multiplied by itself |
| Operation | Multiplication | Inverse operation of squaring |
| Result | Always non-negative for real numbers | Can be positive or negative (principal root is positive) |
| Representation | x² | √x |
8.2. Practical Implications
- Algebraic Equations: Squares and square roots are used to solve equations, with one undoing the effect of the other.
- Geometry: Squares relate to area calculations, while square roots determine lengths from areas.
- Real-World Problems: These concepts appear in various fields, from finance to engineering.
9. Advanced Applications and Examples
Square roots have advanced applications in various mathematical contexts and real-world scenarios.
9.1. Examples in Geometry
- Finding the Diagonal of a Square: If a square has a side length of ‘a’, the diagonal ‘d’ can be found using the formula d = a√2.
- Calculating the Radius of a Circle: If the area of a circle is known (A), the radius ‘r’ can be calculated using the formula r = √(A/π).
- Pythagorean Theorem: In a right triangle, the length of the hypotenuse ‘c’ is given by c = √(a² + b²), where ‘a’ and ‘b’ are the lengths of the other two sides.
9.2. Examples in Physics
- Calculating Velocity: The velocity ‘v’ of an object can be found using the formula v = √(2KE/m), where KE is the kinetic energy and ‘m’ is the mass.
- Determining Time Period of a Pendulum: The time period ‘T’ of a simple pendulum is given by T = 2π√(L/g), where ‘L’ is the length of the pendulum and ‘g’ is the acceleration due to gravity.
9.3. Examples in Computer Science
- Graphics Algorithms: Square roots are used in algorithms for rendering 3D graphics, calculating lighting and shadows, and determining distances.
- Data Analysis: Square roots are employed in statistical analysis, such as calculating standard deviations and variances.
10. Common Mistakes and How to Avoid Them
Learning about square roots can be challenging, and it’s common to make mistakes along the way. Here are some frequent errors and tips on how to avoid them.
10.1. Common Mistakes
- Forgetting Negative Roots: When solving equations, remember that every positive number has two square roots: one positive and one negative.
- Misunderstanding Imaginary Numbers: Incorrectly applying the imaginary unit ‘i’ when dealing with the square roots of negative numbers.
- Simplifying Incorrectly: Making errors in the prime factorization process, leading to incorrect simplification.
- Applying Formulas Incorrectly: Misusing or misunderstanding the properties of square roots.
10.2. How to Avoid Mistakes
- Practice Regularly: Consistent practice helps reinforce the correct methods and formulas.
- Double-Check Calculations: Always double-check your calculations to catch errors in prime factorization and simplification.
- Understand the Theory: A solid understanding of the theoretical concepts behind square roots and imaginary numbers is crucial.
- Seek Help When Needed: Don’t hesitate to ask for help from teachers, tutors, or online resources when you encounter difficulties.
FAQ: Frequently Asked Questions About Square Roots
To further clarify any lingering questions, here’s a comprehensive FAQ section covering common inquiries about square roots.
1. What is a square root in math?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 * 3 = 9.
2. How do I calculate the square root of a number?
You can calculate the square root of a number using several methods:
- Prime Factorization: Break the number into prime factors, pair identical factors, and multiply one factor from each pair.
- Long Division: Use the long division method for a step-by-step calculation.
- Estimation: Estimate the square root by finding the nearest perfect squares.
- Calculator: Use a calculator with a square root function.
3. Can a square root be negative?
Yes, a number can have both a positive and a negative square root. For example, both 3 and -3 are square roots of 9. However, the principal square root is usually the positive value.
4. How do I find the square root of a decimal number?
You can find the square root of a decimal number using the long division method or a calculator.
5. What is the symbol for square root?
The symbol for square root is √.
6. How do I multiply two square root values together?
To multiply two square root values (√a and √b), you can use the property: √a √b = √(a b). Then, simplify the resulting square root if possible.
7. What is the formula for calculating the square root of a number?
The formula for calculating the square root of a number ‘y’ is √y = y½.
8. What is the square and square root of a number?
The square of a number is the result of multiplying the number by itself (e.g., 5² = 25). The square root of a number is the value that, when multiplied by itself, gives the original number (e.g., √25 = 5).
9. What method is used to find the square root of non-perfect square numbers?
The long division method is commonly used to find the square root of non-perfect square numbers.
10. How do I find a square root on a calculator?
To find a square root on a calculator, enter the number and press the square root button (√).
11. What are the applications of the square root formula?
Square root formulas are used in various applications, including:
- Geometry: Calculating lengths, distances, and areas.
- Algebra: Solving equations and simplifying expressions.
- Physics: Determining physical quantities like velocity and energy.
- Computer Science: Implementing algorithms for graphics and data analysis.
12. What does the square of a number mean?
The square of a number means multiplying the number by itself. For example, the square of 5 is 5 * 5 = 25.
13. How do I calculate the square root of a negative number?
The square root of a negative number is an imaginary number. To calculate it, use the formula √(-x) = i√x, where ‘i’ is the imaginary unit (√-1).
14. Why is the square of a negative number positive?
The square of a negative number is positive because when you multiply two negative numbers, the result is always positive. For example, (-3) * (-3) = 9.
Unlock Your Mathematical Potential with LEARNS.EDU.VN
At LEARNS.EDU.VN, we are committed to providing comprehensive and accessible educational resources. Our guides on how to learn square roots are designed to empower learners of all levels, from beginners to advanced students. Whether you are aiming to excel in your studies, enhance your professional skills, or simply explore the wonders of mathematics, LEARNS.EDU.VN is here to support you every step of the way.
Ready to take your learning journey to the next level?
- Explore More Articles: Visit our website to discover a wealth of educational content on various subjects.
- Enroll in Courses: Check out our courses for structured learning experiences with expert instructors.
- Join Our Community: Connect with fellow learners and share your knowledge and insights.
Visit LEARNS.EDU.VN today and unlock your full potential.
Contact Us:
Address: 123 Education Way, Learnville, CA 90210, United States
WhatsApp: +1 555-555-1212
Website: LEARNS.EDU.VN
Embrace the power of knowledge with learns.edu.vn and transform your learning experience today!
