Abstract
As RNA sequencing becomes increasingly accessible and affordable, it has emerged as a powerful tool for cancer prognosis. However, building robust predictive models remains a significant challenge, particularly in biomedical contexts where sample sizes are often limited, and feature dimensions are high. To overcome these limitations, we introduce a meta-learning framework grounded in neural networks for survival analysis, evaluating its efficacy within a genomic cancer research setting. Our findings demonstrate that meta-learning surpasses traditional transfer learning in leveraging high-dimensional, relevant data to address specific problems. Meta-learning excels by constructing a model from abundant data across related tasks, enabling efficient learning on new tasks even with limited samples. In the application of cancer survival outcome prediction, we show that our meta-learning framework, even with few samples, achieves performance levels comparable to models trained from scratch with substantially larger datasets. Furthermore, we reveal that meta-learning models inherently prioritize genes based on their importance for survival prediction, offering insights into crucial cancer pathways.
Subject terms: Cancer genomics, Computational models, Machine learning, Meta-learning, C-index, Hyperparameter Optimization, Survival Analysis
RNA-sequencing data derived from tumors offers a valuable resource for predicting patient prognosis. This study highlights the effectiveness of a neural network meta-learning approach in enhancing prognostic predictions, especially when dealing with small sample sizes, emphasizing the importance of Improving C-index In Meta Learning Model Hyperparameters.
Introduction
Cancer remains a leading cause of mortality worldwide. Accurate prediction of cancer survival outcomes is a critical and complex challenge in ongoing cancer research. Over the decades, various quantitative methods have been developed to model the relationship between multiple variables and survival outcomes, including fully parametric models1,2 and semi-parametric models, most notably the Cox proportional hazards model3. The Cox model, while assuming a parametric relationship between predictors and the hazard function, notably avoids assumptions about the baseline hazard function itself4. In real-world scenarios, the true hazard function’s form is often unknown or excessively complex, making the Cox model the most widely used method in survival analysis5.
Historically, clinical survival analysis has relied on low-dimensional patient characteristics such as age, sex, clinical features, and histopathological evaluations like stage and grade6. Advances in high-throughput sequencing technologies have broadened the availability of high-dimensional genomic data, enabling the discovery of molecular biomarkers to refine survival predictions and improve treatment strategies. The decreasing cost of RNA sequencing, dropping from an average of $100M per genome in 2001 to approximately $1k per genome in 20157, is making its application in prognosis increasingly feasible. However, genomic data often includes tens of thousands of variables, necessitating the development of algorithms capable of effectively handling high dimensionality.
To address these challenges, several regularized Cox models have been proposed8–10. Regularization adds a penalty for model complexity to the Cox partial likelihood, reducing the risk of overfitting. More recently, the enhanced modeling capabilities of deep learning networks have facilitated the creation of survival analysis platforms suitable for high-dimensional feature spaces. For example, autoencoder architectures have been used to extract relevant features from genomic data for liver cancer prognosis prediction11. The Cox model has also been integrated into neural network frameworks to increase modeling flexibility12–15.
A critical question in studying survival outcomes for rare cancers is whether we can effectively utilize the abundant data from more common, related cancers to improve prediction accuracy. Transfer learning16 is a common approach, where a model trained on one or more abundant cancers is fine-tuned for a related target task (a rare cancer). Transfer learning has shown significant improvements in survival prediction performance17. Deep neural networks applied to biomedical imaging data also benefit from transferring information across datasets. For instance, studies have shown that convolutional neural networks pre-trained on ImageNet data can build effective survival models using histology images18,19.
Meta-learning, a rapidly growing area in deep learning research, directly tackles the challenge of “learning to learn”20,21. Meta-learning models are designed to quickly and efficiently adapt to new tasks, typically with limited exposure to the new task environment. This framework holds the potential for superior adaptation compared to traditional transfer learning, which lacks explicit adaptation mechanisms in its pre-training algorithm. This scenario of limited exposure to new tasks is also known as few-shot learning: generalizing effectively from very few examples (shots) from a new task17. Recent advancements in meta-learning have demonstrated its greater effectiveness over transfer learning in few-shot classification22,[23](#CR23], regression[20](#CR20], and reinforcement learning24,20. In this study, we propose a neural network-based meta-learning framework for survival analysis in cancer research. Specifically, in predicting survival outcomes, we demonstrate that our method is preferable to regular transfer learning and other competitive methods across three cancer datasets when training samples for the target cancer are scarce. Finally, we show that the meta-learning model implicitly prioritizes genes based on their contribution to survival prediction, enabling the identification of biological pathways associated with cancer survival outcomes, and highlighting the importance of improving c-index in meta learning model hyperparameters.
Methods
Datasets
We utilized RNA-sequencing data from The Cancer Genome Atlas (TCGA) pan-cancer datasets25. Genes with NA values were removed, and the data was normalized using log transformation and z-score transformation. The resulting dataset comprised 17,176 genes across 9707 samples from 33 cancer types. The outcome variable was survival time in months, with 78% of patients censored.
Survival Prediction Model
Several approaches are commonly used to describe the effect of variables on survival time13. The Cox-PH model3 is the most popular, a semi-parametric proportional hazards model where patient hazards are linearly dependent on patient features, and relative risks are expressed as hazard ratios. Survival trees and random survival forests offer a non-parametric alternative to Cox models26, extending classification and regression trees and random forests for time-to-event data. Artificial neural networks (ANNs) have also been used for survival prediction, often converting survival time into binary or discrete variables and framing prediction as a classification problem27,28. To address potential accuracy loss, ANNs based on proportional hazards have been recently developed. These have demonstrated superior performance with high-dimensional RNA-seq data compared to Cox-PH models (including Ridge and LASSO regularization), random survival trees, and other ANN-based models13. Their direct integration of meta-learning optimization algorithms makes them the most suitable model structure for our framework, especially when improving c-index in meta learning model hyperparameters is a primary goal.
Meta-Learning
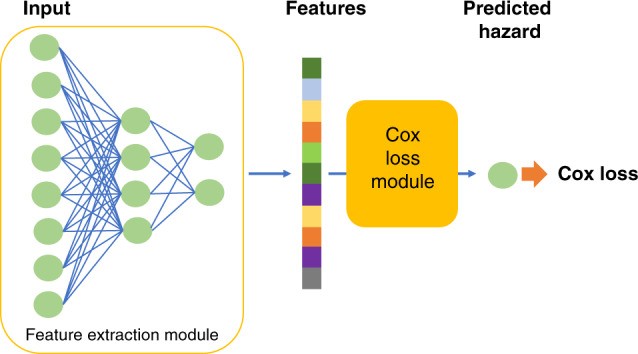
Our proposed survival prediction framework uses a neural network extension of the Cox regression model, relying on semi-parametric modeling with a Cox loss13. The model consists of a feature extraction network and a Cox loss module (Fig. 1). We employ a two-hidden-layer neural network to extract features from RNA sequencing data, yielding a lower-dimensional feature vector for each patient. These features are then input into the Cox loss module, which performs survival prediction using Cox regression with features as linear predictors of hazard3. The Cox loss module parameters β are optimized by minimizing the negative partial log-likelihood:
| L(β)=−∑yi=uncensoredziβ−log∑yj≥yiezjβ, | 1 |
|---|

where *yi is survival length for patient i*, *zi contains extracted features for patient i*, and β is the coefficient weight vector. As **z**i is the output of the feature extraction module:
| zi=fφxi, | 2 |
|---|
where x*i is the input predictor for patient i, f is the nonlinear mapping learned by the neural network, and φ* represents model parameters (weights and biases). The feature extraction module parameters φ and Cox loss module parameters β are jointly trained, denoted as combined parameters θ.
Fig. 1. Survival Prediction Model Architecture.
The model comprises a feature extraction module and a Cox loss module, essential for improving c-index in meta learning model hyperparameters.
Parameter optimization (θ) occurs in two stages: meta-learning and final learning. Meta-learning is crucial, aiming to learn suitable parameter initialization for the final stage, enabling efficient adaptation to new, unseen tasks with few training samples29. A first-order gradient-based meta-learning algorithm trains the network during meta-learning20,29.
Initially, the model is randomly initialized with parameter θ. Training samples for meta-learning include n tasks *Tτ, τ = 1, 2…n. A task is a common learning theme within a sample subgroup. The algorithm samples a task Tτ and updates the inner-learner using its samples. The inner-learner learns T*τ via k steps of stochastic gradient descent (SGD), updating parameters to θτk:
| θτ0=θθτ1←θτ0−αLτ,0′θτ0θτ2←θτ1−αLτ.1′θτ1…θτk←θτk−1−αLτ,k−1′θτk−1, | 3 |
|---|
where θτk is the parameter at step k for task τ, Lτ,k−1 is the loss on the kth minibatch from task τ, and α is the inner learner step size. This learning is separate for all tasks, starting from the same θ.
After m (<n) tasks are independently learned via k-step SGD, yielding θτk, τ = 1, 2, … m, a meta-learner update across these m tasks improves initialization θ:
| θ←θ+γ1m∑τ=1m(θτk−θ), | 4 |
|---|
where γ is the meta-learner’s learning step. The term 1m∑τ=1m(θτk−θ) is a gradient, allowing optimization algorithms like Adam30 to adjust learning rates. Inner-learner and meta-learner updates repeat until a maximum number of meta-learning epochs is reached. This algorithm encourages gradient alignment from different minibatches of a task, improving generalization and efficient learning29, crucial for improving c-index in meta learning model hyperparameters.
In the final learning stage, the model receives a few-sample dataset for a new task. Initialized with meta-learnt parameters θ, it is fine-tuned with new task training data to θτk′. The fine-tuned model is then evaluated using testing data from the new task. Final learning training uses regular mini-batch stochastic gradient descent, similar to the inner-learning loop in Eq. (3) for a single task without an outer loop.
Algorithm 1 summarizes the complete procedure for meta-learning for few-shot survival prediction, ultimately improving c-index in meta learning model hyperparameters.
Algorithm 1: Meta-learning for Few-Shot Survival Prediction
| Initialize randomly θ = {ϕ, β}, feature extractor and Cox model parameters. |
|---|
| Define survival loss function as in Eq. (1): L=−∑yi=uncensoredfφ(xi)β−log∑yj≥yiefφ(xj)β |
| for i ← 0 to n do |
| for m randomly sampled tasks *T*τ do |
| Compute θτk, with k update steps using L, as in Eq. (3) |
| end |
| Update θ←θ+γ1m∑τ=1m(θτk−θ) |
| i ← i + m |
| end |
| Return θ |
Experimental Setup
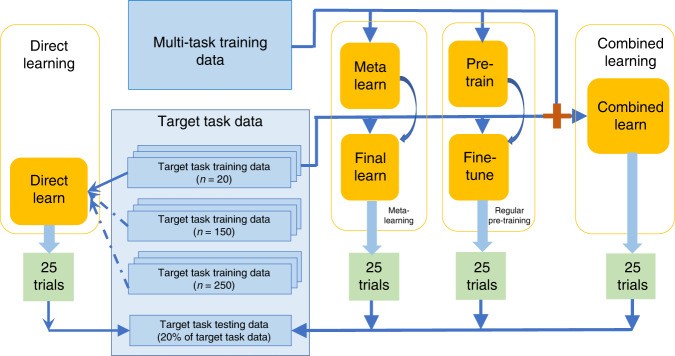
To evaluate meta-learning performance, we compared it with regular pre-training, combined learning, and direct learning, all using the same neural network architecture. Meta-learning learns general knowledge from relevant but not directly related tasks (“multi-task training data”) before learning task-specific knowledge from a small target task dataset (“target task training data”). Regular pre-training also uses a two-stage process on the same datasets but lacks explicit focus on adaptation. Combined learning uses a single-stage process, leveraging knowledge by combining both datasets. Direct learning uses only the target task training samples. To illustrate effectiveness with few samples, we considered direct learning with large, medium, and small sample sizes, the latter matching the “target task training data” size for other methods (Fig. 2).
Fig. 2. Data Flow Schematic.
Data flow for different learning frameworks, crucial for understanding the context of improving c-index in meta learning model hyperparameters. 25 trials were conducted for each framework.
“Multi-task training data” was pan-cancer RNA sequencing data excluding samples from the target cancer site. Target cancer data was “target task data,” split into training and testing sets, stratified by disease sub-type and censoring status. For meta-learning, pre-training, and combined learning, only 20 samples from the target task training dataset were used as “target task training data” to assess performance with limited samples, a realistic scenario for rare diseases31 or new technologies with small sample capacities. For direct learning, we used small (20), medium (150), and large (250) sample sizes. All methods were evaluated on the same target task testing data.
A linear Cox regression model, trained on the combined learning training sample, served as a linear baseline. We conducted 25 trials for each method, each with a randomly drawn “target task training dataset.”
Evaluation
Survival prediction model performance was evaluated using the concordance index (C-index)4 and the integrated Brier score (IBS)32. The C-index measures predictive ability by assessing correctly ordered pairs of subjects, with 1.0 indicating perfect prediction and 0.5 random prediction. IBS evaluates prediction error as the mean squared difference between observed and predicted survival probabilities, with 0 indicating perfect prediction and 1 inaccurate prediction. These metrics are essential for quantifying the success of improving c-index in meta learning model hyperparameters.
Target cancer sites were selected from TCGA based on: (1) minimum 450 samples and (2) minimum 30% non-censoring samples. This included glioma (GBM and LGG), non-small cell lung cancer (LUAD and LUSC), and head-neck squamous cell carcinoma (HNSC). Mesothelioma (MESO), a rare cancer cohort with <90 samples, was used for small sample validation, comparing only to small sample direct learning.
An independent non-small cell lung cancer cohort from Stanford University School of Medicine and Palo Alto Veterans Affairs Healthcare System37 (NCBI GEO38) was used for independent validation. Meta-learning, pre-training, and combined learning models trained with TCGA data were tested on this cohort.
For large target cancer cohorts, 20% of target data was used for testing across 25 trials. For small cancer and independent cohorts, 50% was used for testing across 10 trials due to limited training samples.
Hyperparameter Selection
To prevent overfitting, hyperparameters were selected using 5-fold cross-validation on the largest cancer cohort, glioma, and applied across all experiments. For each hyperparameter set, results from five validation sets (20% of training data each) were averaged. Hyperparameters were shared across methods where applicable due to algorithm similarities. This rigorous selection process is vital for improving c-index in meta learning model hyperparameters.
All methods used a neural network with two hidden fully connected layers (sizes 6000 and 2000) and a 200-size output feature layer, each using ReLU activation39. Initial experiments tested 1 or 2 hidden layers with feature sizes of 200 or 50. The chosen architecture was used for all subsequent methods.
For regular pre-training, hyperparameters for pre-training and fine-tuning stages were searched separately, testing mini-batch gradient descent and Adam optimizers, learning rates (grids of [0.1, 0.05, 0.01, 0.005, 0.001] for SGD and [0.001, 0.0005, 0.0001, 0.00005, 0.00001] for Adam), and batch sizes (50, 100, 200, 800) for pre-training. Selected parameters for pre-training: SGD optimizer, 0.001 learning rate, 0.1 L2 regularization, 800 batch size. Fine-tuning: SGD optimizer, 0.001 learning rate, 0.1 L2 regularization, 20 batch size. Combined and direct learning used pre-training parameters, with batch sizes for direct learning being half the training data size.
For meta-learning, hyperparameter search focused on the meta-learning stage. Final learning used the same hyperparameters as regular pre-training’s fine-tuning stage. Meta-learning stage optimizers included SGD and Adam. Grid search for learning rates ([0.1, 0.05, 0.01, 0.005, 0.001] for SGD and [0.001, 0.0005, 0.0001, 0.00005, 0.00001] for Adam), batch sizes ([50, 100, 200, 800]), tasks for meta-learner update averaging ([5, 10, 20]), and inner-learner gradient descent steps ([3, 5, 10, 20]) were conducted. Selected meta-learning stage parameters are in Table 1.
Table 1. Selected Hyperparameters for Meta-Learning Stage.
| Hyper-parameter | Value |
|---|---|
| Task-level optimizer | SGD |
| Task-level learning rate | 0.01 |
| Task-level gradient steps | 5 |
| Task-level Batch size | 100 |
| Meta-level optimizer | ADAM |
| Meta-level learning rate | 0.0001 |
| Meta-level tasks batch size | 10 |
| L2 regularization scale | 0.1 |
To assess hyperparameter fluctuation effects, tests on validation data varied five unique meta-learning hyperparameters, tuning each up and down by one grid, yielding 10 varied sets. 5-fold cross-validation for each set and 50 random experiments using selected hyperparameters were conducted. A two-sample t-test showed no significant difference between varied and selected hyperparameter results (mean C-index difference 0.005, p = 0.50), indicating result robustness and validating our approach to improving c-index in meta learning model hyperparameters without excessive tuning.
Gene Prioritization Interpretation
Risk score backpropagation15 was applied to meta-learned models to investigate gene feature importance for each cancer site. For each sample, input features were assigned risk scores (partial derivatives of risk). Positive high-value risk scores indicated importance in poor prediction (high risk), negative high-value scores in good prediction (low risk). Features were ranked by average risk score across samples.
Two approaches annotated ranked risk score genes. First, top 10% high-risk (positive scores) and low-risk (negative scores) genes per cancer type underwent gene set over-representation analysis, comparing against gene sets with defined functions using hypergeometric distribution and Fisher’s exact test. Second, gene set enrichment analysis with the fgsea R package40 incorporated all genes and ranked risk scores, calculating a cumulative enrichment statistic for each gene set. Gene set databases included KEGG41, Reactome[42](#CR42], and WikiPathways43. This analysis is crucial for understanding the biological relevance of improving c-index in meta learning model hyperparameters.
Results
Meta-Learning Outperforms Pre-training and Combined Learning
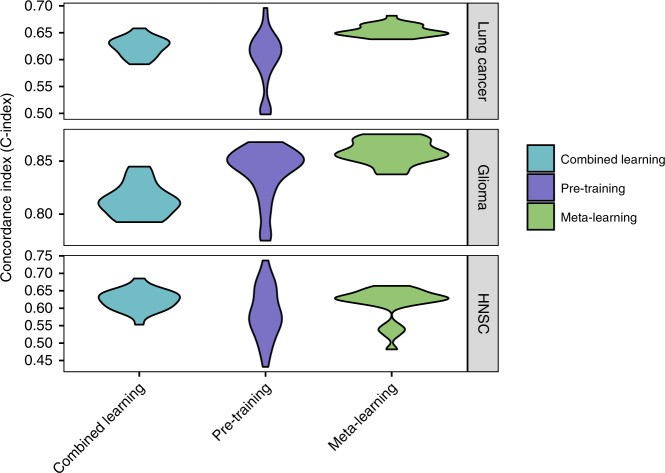
Meta-learning achieved similar or superior performance compared to regular pre-training and combined learning across all large target cancer sites (Fig. 3; Table 2), demonstrably improving c-index in meta learning model hyperparameters. For glioma, meta-learning had a mean C-index of 0.86 (95% CI 0.85–0.86), compared to 0.84 (95% CI 0.83–0.85) for pre-training and 0.81 (95% CI 0.81–0.82) for combined training. For lung cancer, mean C-indices were 0.65 (95% CI 0.65–0.66) for meta-learning, 0.60 (95% CI 0.58–0.61) for pre-training, and 0.62 (95% CI 0.62–0.63) for combined training. For HNSC, results were 0.61 (95% CI 0.59–0.63) for meta-learning, 0.59 (95% CI 0.57–0.61) for pre-training, and 0.62 (95% CI 0.61–0.64) for combined training. Meta-learning results also showed the smallest variance across 25 trials, especially for lung cancer and glioma. All multi-layer neural networks outperformed the linear baseline model, which achieved C-indices of 0.61 for lung cancer (95% CI 0.60–0.62), 0.77 for glioma (95% CI 0.74–0.80), and 0.59 for HNSC (95% CI 0.58–0.62).
Fig. 3. C-Index Comparison for Survival Prediction.
C-Index results for lung cancer, glioma, and head and neck cancer, comparing combined learning, regular pre-training, and meta-learning. The consistent high performance of meta-learning highlights the effectiveness of improving c-index in meta learning model hyperparameters.
Table 2. Integrated Brier Scores (IBS) for Target Cancer Survival Prediction.
| Method | Glioma | Lung cancer | HNSC |
|---|---|---|---|
| Direct (250 samples) | 0.24 ± 0.02 | 0.19 ± 0.01 | 0.20 ± 0.01 |
| Direct (150 samples) | 0.25 ± 0.01 | 0.19 ± 0.01 | 0.21 ± 0.01 |
| Direct | 0.30 ± 0.02 | 0.24 ± 0.02 | 0.30 ± 0.02 |
| Combined | 0.29 ± 0.02 | 0.21 ± 0.02 | 0.26 ± 0.02 |
| Pre-training | 0.31 ± 0.02 | 0.23 ± 0.02 | 0.26 ± 0.02 |
| Meta-learning | 0.28 ± 0.01 | 0.16 ± 0.01 | 0.16 ± 0.00 |
IBS with 95% confidence intervals (n = 25 trials), lower value is better. Best performing method in bold. Meta-learning shows superior IBS, further demonstrating the benefits of improving c-index in meta learning model hyperparameters.
Meta-Learning Achieves Competitive Predictive Performance
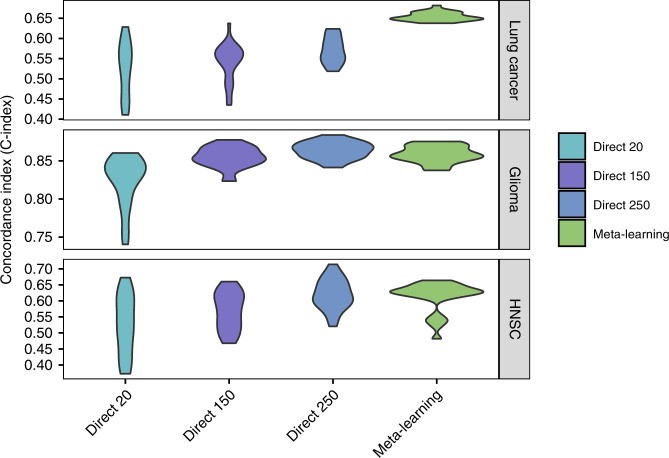
Meta-learning achieved similar or better prediction performance compared to large-sample direct training in lung cancer and HNSC, and comparable performance to medium-sample direct training in glioma (Fig. 4; Table 2). Direct learning performance significantly decreased with fewer training samples. Meta-learning and pre-training compensated for this information loss via knowledge transfer. For lung cancer, mean C-indices were 0.57 (95% CI 0.56–0.58) for large sample direct learning, 0.54 (95% CI 0.52–0.56) for medium sample, 0.53 (95% CI 0.50–0.55) for small sample, and 0.65 (95% CI 0.65–0.66) for meta-learning. For glioma, C-indices were 0.86 (95% CI 0.86–0.87), 0.85 (95% CI 0.85–0.86), and 0.82 (95% CI 0.81–0.84) for large, medium, and small sample direct learning, respectively, and 0.86 (95% CI 0.85–0.86) for meta-learning. For HNSC, C-indices were 0.62 (95% CI 0.60–0.64), 0.57 (95% CI 0.54–0.59), and 0.53 (95% CI 0.49–0.56) for large, medium, and small sample direct learning, and 0.61 (95% CI 0.59–0.63) for meta-learning. Meta-learning consistently reached competitive performance levels, underscoring the efficacy of improving c-index in meta learning model hyperparameters.
Fig. 4. C-Index Comparison with Direct Learning.
C-Index for survival prediction, comparing direct learning with large, medium, and small sample sizes against meta-learning for lung cancer, glioma, and head and neck cancer. Meta-learning’s competitive performance even with small samples highlights the success of improving c-index in meta learning model hyperparameters.
Risk Score Genes Enriched in Key Cancer Pathways
Gene set enrichment analysis of risk-ranked genes revealed significant associations with key cancer pathways (Fig. 5, Supplementary Tables 1–6). In gliomas, high-risk genes were linked to viral carcinogenesis (p = 0.002), Herpes simplex infection (p = 0.007), cell cycle (p = 0.03), apoptosis (p = 0.03), and DNA damage response (p = 0.04), also enriched in gene set enrichment analysis. Low-risk genes were associated with HSF1 activation (p = 0.02) and tryptophan metabolism (p = 0.04), the latter also enriched in gene set enrichment analysis with negative scores.
Fig. 5. Gene Set Enrichment Analysis.
Gene set enrichment analysis in Glioma, Head and neck cancer, and Lung cancer. Enriched pathways with p value below 0.05 or 0.01 are displayed. These insights into gene pathways further validate the effectiveness of improving c-index in meta learning model hyperparameters.
In head and neck cancer, high-risk genes were associated with PTK6 signaling (p = 0.01) and inflammatory response (p = 0.009). Low-risk genes were linked to autophagy (p = 0.02), also enriched in gene set enrichment analysis, along with B cell receptor signaling, cell cycle, and interleukin 1 signaling.
In lung cancer, high-risk genes were associated with “non-small cell lung cancer” pathway (p = 0.01), tuberculosis (p = 0.008), Hepatitis B and C virus infection (p = 0.03), and other cancer-related pathways, all enriched in gene set enrichment analysis. Low-risk genes were associated with energy metabolism (p = 0.03), ferroptosis (p = 0.037), and AMPK signaling (p = 0.046), also enriched in gene set enrichment analysis, along with Notch signaling, interleukin signaling, ErbB signaling, and stem cell pluripotency pathways.
Validation on Rare Cancer Cohort
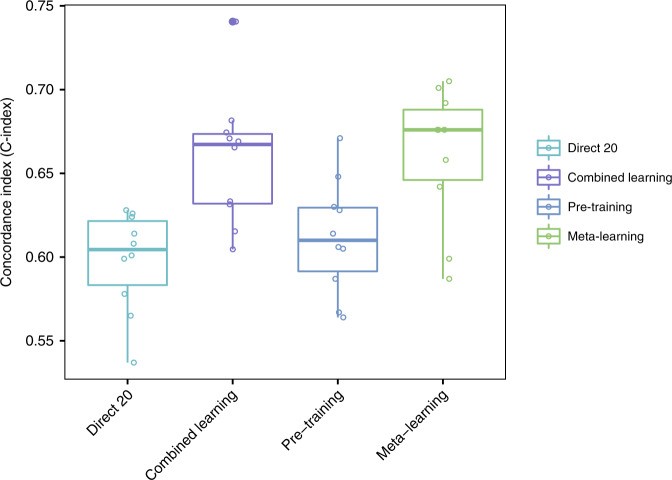
Meta-learning performed similarly or better than pre-training, combined learning, and small sample direct learning on the rare mesothelioma cohort (Fig. 6). Meta-learning’s mean C-index was 0.66 (95% CI 0.63–0.69), compared to 0.62 (95% CI 0.59–0.64) for pre-training, 0.65 (95% CI 0.63–0.67) for combined training, and 0.60 (95% CI 0.59–0.62) for small sample direct learning.
Fig. 6. C-Index on Mesothelioma Cohort.
C-Index for survival prediction on the mesothelioma cohort, comparing different learning methods. Meta-learning’s robust performance in rare cancer prediction further illustrates the advantage of improving c-index in meta learning model hyperparameters.
Validation on Independent Lung Cancer Cohort
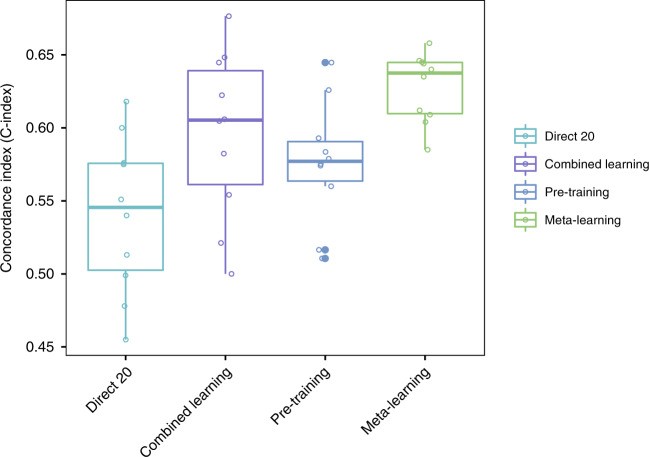
On the independent lung cancer cohort, meta-learning outperformed pre-training, combined learning, and small sample direct learning (Fig. 7). Meta-learning’s mean C-index was 0.63 (95% CI 0.61–0.65), compared to 0.58 (95% CI 0.55–0.61) for pre-training, 0.59 (95% CI 0.55–0.64) for combined training, and 0.54 (95% CI 0.50–0.58) for small sample direct learning.
Fig. 7. C-Index on Independent Lung Cancer Cohort.
C-Index for survival prediction on an independent lung cancer cohort. Meta-learning’s superior performance on independent data validates the generalization and effectiveness of improving c-index in meta learning model hyperparameters.
Discussion
Deep learning survival models have shown comparable or superior performance to other methods in high-dimensional genomic data analysis49. However, their performance is often limited by small datasets15. This study explored deep learning paradigms to improve performance, especially with small training datasets, focusing on improving c-index in meta learning model hyperparameters.
Direct training with large samples is a baseline, but its performance declines with smaller sample sizes. Combined learning, pre-training, and meta-learning leverage external data, improving performance with small samples. Meta-learning outperformed combined and pre-training, indicating better adaptation due to its optimization algorithm.
While Bayesian meta-learning is an option for small meta-training sample sizes50,51, its high-dimensional improvements are marginal51. Combined learning, pre-training, and meta-learning use the same information but differ algorithmically. Meta-learning’s superior performance indicates more effective adaptation in few-sample environments, directly linked to improving c-index in meta learning model hyperparameters.
Performance differences between methods using only target task data and those using additional data vary across cancer sites. Glioma favored direct learning; lung cancer benefited from other methods. This reflects varying information content in target vs. related data. Meta-learning performed comparably to medium-size direct training and outperformed large-size direct training in some cases. However, meta-learning advantages may not generalize to all cancers due to unique cancer characteristics limiting information transfer. For kidney cancer (KIRC and KIRP), meta-learning and pre-training performed poorly, visualized in Supplementary Fig. 1 showing affinity between cancers via t-SNE. Effective meta-learning requires transferable information from related tasks, and the focus on improving c-index in meta learning model hyperparameters becomes crucial in such scenarios.
Meta-learning’s performance is attributed to its learned learning algorithm. Sampling approaches within tasks influence performance; mixing samples from multiple cancer types improved results. Gradient analysis suggests the algorithm encourages gradient alignment, benefiting generalization when minibatches contain diverse cancer types.
Cancer type interdependencies exist. Multi-task training data includes interdependent cancer sites. While we focused on information transfer, handling cross-task relations in meta-learning could further improve generalization. Recent methods addressing task relations53 warrant future investigation, especially in the context of improving c-index in meta learning model hyperparameters.
Gene set enrichment analysis validated gene prioritization. Enriched pathways in investigated cancers included cell cycle regulation, DNA damage response, cell death, and signaling pathways.
Besides known cancer pathways, our results suggest potential roles for viruses in glioma and lung cancer, with high-risk genes enriched in viral carcinogenesis pathways. Glioma high-risk pathways included Epstein-Barr virus and herpes simplex infection. Lung cancer high-risk pathways included hepatitis B and C virus infection. Metabolic pathways, particularly lipid metabolism, were favorable for survival in all three cancers. Glioma survival-favorable pathways included adipogenesis regulation. Head and neck cancer included adipocyte differentiation and fatty acid biosynthesis. Lung cancer included ferroptosis and AMPK signaling.
In conclusion, meta-learning effectively addresses the issue of limited training samples in survival analysis, achieving similar performance to larger datasets through efficient knowledge transfer. It surpasses pre-training and combined learning in predictive performance with limited samples and offers interpretable models for investigating cancer survival biology, particularly when improving c-index in meta learning model hyperparameters is prioritized.
Small data sizes limit many biomedical analyses. Meta-learning shows promise for biomedical applications in alleviating data limitations. Future work will extend this approach to medical imaging data for multi-modal predictive models with limited patient sets.
Reporting summary
Further research design information is available in the Nature Research Reporting Summary.
Supplementary Information
Supplementary Information (2.3MB, pdf)
Reporting Summary (314.5KB, pdf)
Acknowledgements
A.D. acknowledges funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 754354.
Author contributions
Y.L.Q., A.D., and O.G. conceived of the presented idea and designed the computational framework. Y.L.Q. performed the analytic experiments. H.Z. carried out genetic analysis. H.S. contributed to the preparation of data. All authors discussed the results and contributed to the final manuscript.
Data availability
All data used are publicly available. TCGA Gene expression data is version 2, adjusted pan-cancer gene expression data from Synapse: https://www.synapse.org/#!Synapse:syn4976369.2. Independent lung cancer data from: https://wiki.cancerimagingarchive.net/display/Public/NSCLC+Radiogenomics. Gene set enrichment analysis databases: KEGG (https://www.genome.jp/kegg/), Reactome (https://reactome.org/download-data), and WikiPathways (https://www.wikipathways.org/index.php/Download_Pathways). Remaining data within the Article, Supplementary Information, or from authors upon request.
Code availability
Code is in the GitHub repository: https://github.com/gevaertlab/metalearning_survival62.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review information Nature Communications thanks Dipak Dey and the other, anonymous, reviewer(s) for their contribution.
Publisher’s note Springer Nature remains neutral to jurisdictional claims.
Supplementary information
Supplementary information is available at 10.1038/s41467-020-20167-3.
References
[References]
Associated Data
Supplementary Materials
Supplementary Information (2.3MB, pdf)
Reporting Summary (314.5KB, pdf)
Data Availability Statement
All data used are publicly available. TCGA Gene expression data is version 2, adjusted pan-cancer gene expression data from Synapse: https://www.synapse.org/#!Synapse:syn4976369.2. Independent lung cancer data from: https://wiki.cancerimagingarchive.net/display/Public/NSCLC+Radiogenomics. Gene set enrichment analysis databases: KEGG (https://www.genome.jp/kegg/), Reactome (https://reactome.org/download-data), and WikiPathways (https://www.wikipathways.org/index.php/Download_Pathways). Remaining data within the Article, Supplementary Information, or from authors upon request.
Code is in the GitHub repository: https://github.com/gevaertlab/metalearning_survival62.