Do You Need To Know Linear Algebra For Machine Learning?

Do You Need To Know Linear Algebra For Machine Learning? Absolutely, grasping linear algebra is crucial for anyone serious about machine learning, and LEARNS.EDU.VN can help you master these essential concepts. This article will provide you with a detailed overview of linear algebra, focusing on its practical applications in machine learning, equipping you with the knowledge and skills to excel in this dynamic field with comprehensive resources, tutorials, and expert guidance. Explore key concepts, applications, and resources to excel in machine learning with linear algebra.

1. Introduction to Linear Algebra in Machine Learning

Linear algebra is a cornerstone of mathematics, providing the framework to model and solve complex problems across science, engineering, and, crucially, machine learning. Its strength lies in its ability to efficiently handle and manipulate large datasets, a common requirement in machine learning.

1.1. What is Linear Algebra?

Linear algebra deals with linear equations and their representations through matrices and vectors. It’s not just about abstract math; it’s a practical toolkit for solving real-world problems.

1.2. Why is Linear Algebra Important for Machine Learning?

Understanding linear algebra is vital for several reasons:

• Algorithm Understanding: It provides insights into how machine learning algorithms function internally.
• Data Handling: It helps in representing and manipulating data efficiently.
• Problem Solving: It enables the optimization and tuning of machine learning models.
• Foundation for Advanced Topics: Crucial for grasping deep learning, neural networks, and more.

1.3. The Role of Linear Algebra in Machine Learning

Linear algebra is the backbone of many machine learning algorithms. It is used in data preprocessing, dimensionality reduction, model training, and evaluation. Understanding linear algebra allows you to make informed decisions about algorithm selection and parameter tuning.

Examples of Linear Algebra in Machine Learning

Application	Description	Linear Algebra Concepts Involved
Data Representation	Representing datasets as matrices where rows are samples and columns are features.	Matrices, Vectors
Dimensionality Reduction	Techniques like Principal Component Analysis (PCA) use eigenvalue decomposition to reduce data dimensions.	Eigenvalues, Eigenvectors, Decomposition
Model Training	Solving systems of linear equations to find the optimal parameters for linear regression models.	Matrix Inversion, System of Equations
Image Processing	Representing images as matrices and applying transformations using matrix operations.	Matrix Operations, Transformations

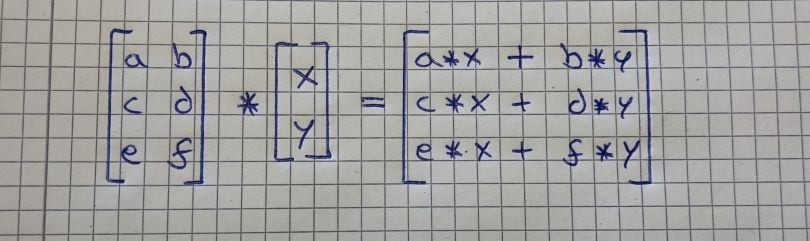
2. Fundamental Concepts of Linear Algebra

To understand its application in machine learning, let’s first look at the basic building blocks of linear algebra.

2.1. Scalars

A scalar is a single number. It’s the simplest element in linear algebra. For example, 5, -3, 2.7, and π are all scalars.

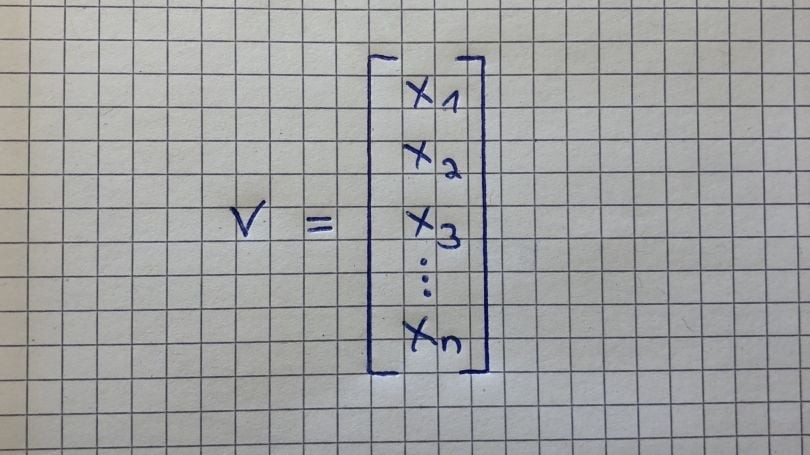
2.2. Vectors

A vector is an ordered array of numbers. It can be represented as a row vector or a column vector. Each number in a vector is called a component or element.

Vector Example:

[1, 2, 3] (row vector)

[
 4
 5
 6
] (column vector)

Vectors are used to represent data points in machine learning. For instance, a vector could represent the features of a single data point, such as the height, weight, and age of a person.

2.3. Matrices

A matrix is a two-dimensional array of numbers. It has rows and columns. The dimensions of a matrix are given as (number of rows) x (number of columns).

Matrix Example:

[
 [1, 2, 3],
 [4, 5, 6],
 [7, 8, 9]
]

This is a 3×3 matrix. Matrices are used to represent datasets, transformations, and relationships between data points.

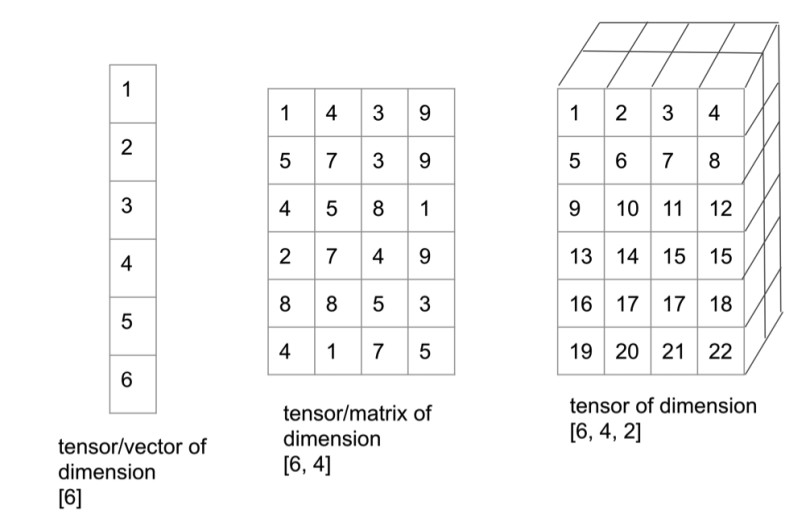
2.4. Tensors

A tensor is a generalization of vectors and matrices to higher dimensions. It is an array of numbers arranged on a regular grid with a variable number of axes.

• A 0th-order tensor is a scalar.
• A 1st-order tensor is a vector.
• A 2nd-order tensor is a matrix.
• Tensors of order 3 and higher are called higher-order tensors.

Tensor Example:

A 3D tensor can be thought of as a cube of numbers. It has rows, columns, and depth. Tensors are used in deep learning to represent images, videos, and other complex data.

2.5. Scalars, Vectors, Matrices, and Tensors: A Hierarchy

To put it simply:

• A Scalar is a single number.
• A Vector is a 1D array of numbers.
• A Matrix is a 2D array of numbers.
• A Tensor is an n-dimensional array of numbers.

Tensors are the most general form, encompassing scalars, vectors, and matrices as special cases.

3. Essential Operations in Linear Algebra

Understanding the operations that can be performed on these mathematical objects is crucial. These operations form the basis for many machine learning algorithms.

3.1. Matrix-Scalar Operations

When you perform an operation between a matrix and a scalar (addition, subtraction, multiplication, or division), the operation is applied to each element of the matrix.

Example:

Scalar: 2
Matrix:
[
 [1, 2],
 [3, 4]
]

Multiplication:
[
 [2*1, 2*2],
 [2*3, 2*4]
]
=
[
 [2, 4],
 [6, 8]
]

3.2. Matrix-Vector Multiplication

Multiplying a matrix by a vector can be thought of as multiplying each row of the matrix by the column of the vector. The result is a vector with the same number of rows as the matrix.

Example:

Matrix:
[
 [1, 2],
 [3, 4]
]
Vector:
[
 5
 6
]

Result:
[
 [1*5 + 2*6],
 [3*5 + 4*6]
]
=
[
 17
 39
]

3.3. Matrix-Matrix Addition and Subtraction

Matrix addition and subtraction are straightforward. The matrices must have the same dimensions, and the operation is performed element-wise.

Example:

Matrix A:
[
 [1, 2],
 [3, 4]
]
Matrix B:
[
 [5, 6],
 [7, 8]
]

Addition:
[
 [1+5, 2+6],
 [3+7, 4+8]
]
=
[
 [6, 8],
 [10, 12]
]

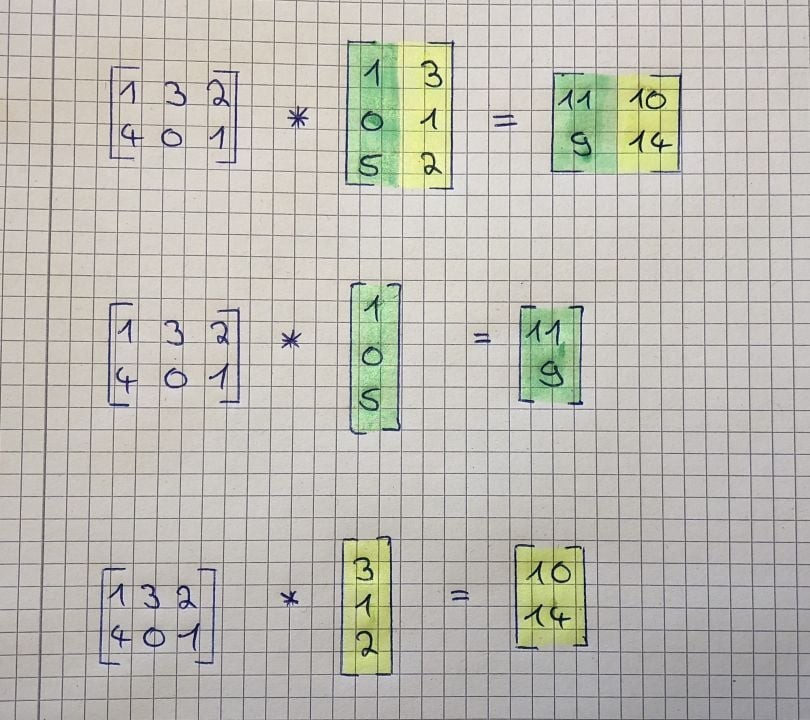
3.4. Matrix-Matrix Multiplication

Matrix multiplication is more complex than addition or subtraction. To multiply two matrices, the number of columns in the first matrix must equal the number of rows in the second matrix.

Example:

Matrix A (2x2):
[
 [1, 2],
 [3, 4]
]
Matrix B (2x2):
[
 [5, 6],
 [7, 8]
]

Result (2x2):
[
 [1*5 + 2*7, 1*6 + 2*8],
 [3*5 + 4*7, 3*6 + 4*8]
]
=
[
 [19, 22],
 [43, 50]
]

4. Key Properties of Matrix Multiplication

Matrix multiplication has several important properties that are used extensively in machine learning.

4.1. Non-Commutativity

Unlike scalar multiplication, matrix multiplication is not commutative. This means that A * B is generally not equal to B * A. The order of multiplication matters.

4.2. Associativity

Matrix multiplication is associative, meaning that A * (B * C) = (A * B) * C. This property allows us to group matrix multiplications in different ways without changing the result.

4.3. Distributivity

Matrix multiplication is distributive over addition, meaning that A * (B + C) = A * B + A * C. This property allows us to distribute a matrix multiplication over a sum of matrices.

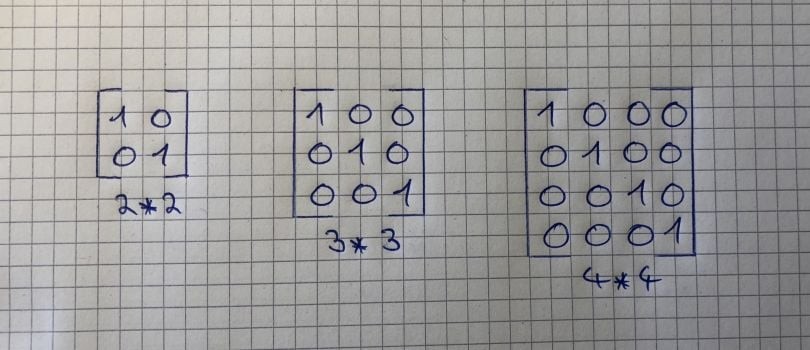
4.4. Identity Matrix

The identity matrix is a square matrix with ones on the main diagonal and zeros everywhere else. When a matrix is multiplied by the identity matrix, the result is the original matrix.

Identity Matrix Example:

[
 [1, 0],
 [0, 1]
]

For any matrix A, A * I = I * A = A, where I is the identity matrix.

5. Advanced Concepts: Inverse and Transpose

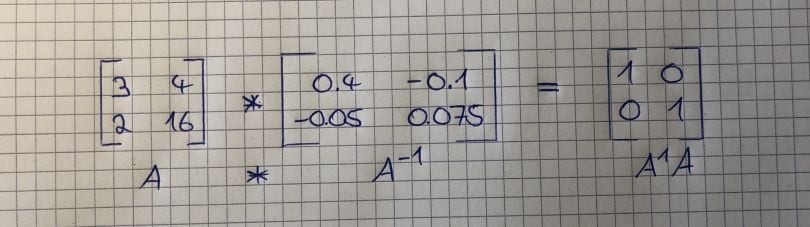
5.1. Matrix Inverse

The inverse of a matrix A, denoted as A^(-1), is a matrix such that when multiplied by A, the result is the identity matrix. Not all matrices have an inverse; only square matrices with a non-zero determinant have an inverse.

A * A^(-1) = A^(-1) * A = I

The inverse of a matrix is used to solve systems of linear equations and perform other important operations in machine learning.

5.2. Matrix Transpose

The transpose of a matrix A, denoted as A^T, is obtained by interchanging the rows and columns of A. The first column of A becomes the first row of A^T, and so on.

Example:

Matrix A:
[
 [1, 2],
 [3, 4],
 [5, 6]
]

Transpose of A:
[
 [1, 3, 5],
 [2, 4, 6]
]

6. Linear Algebra in Machine Learning Algorithms

Linear algebra is not just theoretical; it is applied in various machine learning algorithms.

6.1. Linear Regression

Linear regression is a basic machine learning algorithm that models the relationship between a dependent variable and one or more independent variables by fitting a linear equation to the observed data. Linear algebra is used to solve the linear regression equation efficiently.

• Equation Representation: The linear regression equation can be represented in matrix form as y = Xb + e, where:
  • y is the vector of observed responses.
  • X is the matrix of predictor variables.
  • b is the vector of coefficients to be estimated.
  • e is the vector of errors.
• Solving for Coefficients: The coefficients b that minimize the sum of squared errors can be found using the normal equation:
  • b = (X^T X)^(-1) X^T y

6.2. Principal Component Analysis (PCA)

PCA is a dimensionality reduction technique that transforms high-dimensional data into a lower-dimensional representation while retaining the most important information. It is widely used in machine learning for feature extraction and data preprocessing.

• Covariance Matrix: The first step in PCA involves computing the covariance matrix of the data.

  • The covariance matrix C of a dataset X (where each column is a feature) is calculated as:

  • C = (1/(n-1)) X^T X

  • where n is the number of observations.

• Eigenvalue Decomposition: PCA then performs eigenvalue decomposition on the covariance matrix to find the eigenvectors and eigenvalues.

  • C = VLV^(-1)
  • where V is the matrix of eigenvectors and L is the diagonal matrix of eigenvalues.

• Dimensionality Reduction: The eigenvectors are sorted by their corresponding eigenvalues, and the top k eigenvectors are selected to form a transformation matrix.

  • These top eigenvectors (principal components) capture the most variance in the data.
  • The original data is then projected onto these principal components to obtain a lower-dimensional representation.

6.3. Support Vector Machines (SVM)

SVM is a powerful machine-learning algorithm used for classification and regression tasks. Linear algebra is crucial for understanding and implementing SVM, particularly in the context of kernel methods and optimization.

• Linear SVM: In its simplest form, SVM aims to find the optimal hyperplane that separates data points into different classes with the maximum margin.

  • The decision boundary can be expressed as:

  • w^T x + b = 0

  • where w is the weight vector, x is the input vector, and b is the bias.

• Kernel Methods: SVM can use kernel methods to map data into higher-dimensional spaces where linear separation is possible.

  • Kernel methods rely on linear algebra to compute dot products in the high-dimensional space.
  • Common kernel functions include the polynomial kernel and the radial basis function (RBF) kernel.

6.4. Neural Networks and Deep Learning

Neural networks are at the heart of deep learning, and their operations heavily rely on linear algebra. From forward propagation to backpropagation, understanding linear algebra is essential.

• Forward Propagation: In a neural network, the input data is transformed through multiple layers of interconnected nodes.

  • Each layer performs a linear transformation followed by a non-linear activation function.

  • The linear transformation in each layer can be represented as:

  • z = Wx + b

  • where W is the weight matrix, x is the input vector, and b is the bias vector.

• Backpropagation: The backpropagation algorithm, used to train neural networks, relies on the chain rule of calculus to compute gradients.

  • Linear algebra is used to efficiently compute these gradients and update the weights and biases of the network.

7. Practical Applications of Linear Algebra in Real-World Scenarios

Linear algebra is not just a theoretical concept; it has numerous practical applications in various fields.

7.1. Image Processing

Image processing involves manipulating and analyzing digital images using various techniques. Linear algebra plays a crucial role in image processing tasks such as image representation, filtering, and transformations.

• Image Representation: Digital images can be represented as matrices where each element corresponds to the pixel intensity value.
• Image Filtering: Linear algebra is used to perform image filtering operations, such as blurring and sharpening.
• Image Transformations: Linear algebra is used to perform image transformations such as scaling, rotation, and translation.

7.2. Natural Language Processing (NLP)

NLP involves the analysis and understanding of human language by computers. Linear algebra is used in various NLP tasks such as text representation, sentiment analysis, and machine translation.

• Text Representation: Text data can be represented as vectors using techniques such as bag-of-words and TF-IDF.
• Sentiment Analysis: Linear algebra is used to perform sentiment analysis by analyzing the sentiment scores of words and phrases.
• Machine Translation: Linear algebra is used in machine translation to map words and phrases from one language to another.

7.3. Recommendation Systems

Recommendation systems are used to predict the preferences of users and recommend items that they are likely to be interested in. Linear algebra is used in recommendation systems to perform tasks such as collaborative filtering and matrix factorization.

• Collaborative Filtering: Collaborative filtering is a technique used to predict the preferences of users based on the preferences of similar users.
• Matrix Factorization: Matrix factorization is a technique used to decompose a user-item interaction matrix into lower-dimensional matrices.

7.4. Robotics and Computer Graphics

Robotics and computer graphics rely heavily on linear algebra for tasks such as object transformations, simulations, and rendering.

• Object Transformations: Linear algebra is used to perform object transformations such as translation, rotation, and scaling.
• Simulations: Linear algebra is used to simulate the behavior of physical systems in robotics and computer graphics.
• Rendering: Linear algebra is used to render 3D scenes by projecting them onto a 2D screen.

8. Tools and Libraries for Linear Algebra in Machine Learning

To effectively apply linear algebra in machine learning, you need to be familiar with the right tools and libraries. These tools provide efficient implementations of linear algebra operations and make it easier to work with large datasets.

8.1. NumPy

NumPy is a fundamental package for scientific computing in Python. It provides support for arrays and matrices, as well as a large collection of mathematical functions to operate on these arrays.

• Arrays and Matrices: NumPy’s core data structure is the ndarray, a multi-dimensional array that can represent vectors, matrices, and tensors.
• Mathematical Functions: NumPy provides a wide range of mathematical functions for performing linear algebra operations, such as matrix multiplication, eigenvalue decomposition, and singular value decomposition.

8.2. SciPy

SciPy is another important library for scientific computing in Python. It builds on NumPy and provides additional functionality for linear algebra, optimization, and other tasks.

• Linear Algebra Routines: SciPy’s linalg module provides a comprehensive set of linear algebra routines, including solvers for linear systems, eigenvalue problems, and matrix decompositions.

8.3. TensorFlow and PyTorch

TensorFlow and PyTorch are popular deep-learning frameworks that provide support for tensor operations and automatic differentiation. They are widely used in the development of neural networks and other machine-learning models.

• Tensor Operations: TensorFlow and PyTorch provide optimized implementations of tensor operations, such as matrix multiplication, convolution, and pooling.
• Automatic Differentiation: TensorFlow and PyTorch automatically compute gradients of tensor operations, which is essential for training neural networks.

9. Learning Resources for Linear Algebra

Many resources are available to help you learn linear algebra and its applications in machine learning.

9.1. Online Courses

• Khan Academy: Khan Academy offers free video lessons and practice exercises on linear algebra.
• Coursera and edX: Platforms like Coursera and edX offer courses on linear algebra taught by university professors.

9.2. Textbooks

• “Linear Algebra and Its Applications” by Gilbert Strang: A popular textbook that provides a comprehensive introduction to linear algebra.
• “Deep Learning” by Ian Goodfellow, Yoshua Bengio, and Aaron Courville: A book covering the mathematical background needed for deep learning, including linear algebra.

9.3. Online Tutorials and Blogs

• Machine Learning Mastery: A website that offers tutorials on linear algebra for machine learning.
• LEARNS.EDU.VN: Offers articles and tutorials on linear algebra and its applications in machine learning.

10. Common Questions About Linear Algebra for Machine Learning

To help you better understand the role of linear algebra in machine learning, here are answers to some frequently asked questions.

10.1. Is Linear Algebra Necessary for All Machine Learning Tasks?

No, but understanding linear algebra can significantly enhance your ability to grasp and optimize machine learning algorithms. For basic tasks, you can often rely on pre-built libraries and tools, but for more advanced work, a solid foundation in linear algebra is essential.

10.2. What Level of Linear Algebra is Required?

A basic understanding of vectors, matrices, and matrix operations is sufficient for many machine learning tasks. However, for more advanced work, you may need to delve into topics such as eigenvalue decomposition, singular value decomposition, and optimization techniques.

10.3. Can I Learn Linear Algebra While Learning Machine Learning?

Yes, many people find it helpful to learn linear algebra alongside machine learning. This approach allows you to see the practical applications of linear algebra concepts and reinforces your understanding.

10.4. What Are Some Common Mistakes to Avoid When Using Linear Algebra in Machine Learning?

• Incorrect Matrix Dimensions: Ensure that the dimensions of matrices are compatible for multiplication and other operations.
• Misunderstanding Eigenvalues and Eigenvectors: Understand the meaning and properties of eigenvalues and eigenvectors in the context of PCA and other dimensionality reduction techniques.
• Ignoring Numerical Stability: Be aware of numerical stability issues when performing matrix inversions and other operations on large matrices.

11. The Future of Linear Algebra in Machine Learning

As machine learning continues to evolve, linear algebra will remain a fundamental tool. With the rise of deep learning and other advanced techniques, the importance of linear algebra is only set to increase.

11.1. Emerging Trends

• Quantum Linear Algebra: Quantum computing has the potential to revolutionize linear algebra by providing exponential speedups for certain matrix operations.
• Tensor Decomposition: Tensor decomposition techniques are being developed to handle high-dimensional data in machine learning.
• Optimization Algorithms: New optimization algorithms based on linear algebra are being developed to train machine learning models more efficiently.

11.2. Continued Importance

Linear algebra will continue to be a vital tool for understanding and developing machine learning algorithms. As the field advances, a strong foundation in linear algebra will be essential for researchers and practitioners.

12. FAQ: Linear Algebra for Machine Learning

1. Why is linear algebra important for machine learning?

Linear algebra is crucial because it provides the mathematical foundation for many machine learning algorithms, enabling efficient data representation, manipulation, and problem-solving.

2. What are the basic concepts of linear algebra that I should know for machine learning?

You should understand scalars, vectors, matrices, tensors, matrix operations (addition, subtraction, multiplication), matrix properties (transpose, inverse), eigenvalues, and eigenvectors.

3. How is linear algebra used in linear regression?

Linear algebra is used to solve the linear regression equation efficiently by representing the equation in matrix form and using matrix operations to find the optimal coefficients.

4. Can you explain how PCA uses linear algebra?

PCA uses eigenvalue decomposition to find the principal components of the data, which are the eigenvectors of the covariance matrix sorted by their corresponding eigenvalues.

5. What role does linear algebra play in neural networks?

Linear algebra is used extensively in neural networks for forward propagation (linear transformations of input data) and backpropagation (computing gradients and updating weights).

6. What are the best tools for performing linear algebra operations in machine learning?

NumPy and SciPy in Python are excellent tools. TensorFlow and PyTorch also provide robust support for tensor operations, which are essential in deep learning.

7. How do I apply linear algebra in image processing?

In image processing, linear algebra is used to represent images as matrices, perform filtering operations, and apply transformations such as scaling, rotation, and translation.

8. What is the identity matrix and why is it important?

The identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere. It is important because multiplying any matrix by the identity matrix results in the original matrix.

9. Where can I find good resources to learn linear algebra for machine learning?

You can find resources on Khan Academy, Coursera, edX, and in textbooks like “Linear Algebra and Its Applications” by Gilbert Strang. Also, check out LEARNS.EDU.VN for relevant articles and tutorials.

10. What is a matrix transpose and how is it used?

The transpose of a matrix is obtained by interchanging its rows and columns. It is used in various applications, such as calculating the covariance matrix in PCA and representing data in different forms.

13. Conclusion: Mastering Linear Algebra for Machine Learning Success

Linear algebra is more than just an academic subject; it is a practical and essential tool for anyone working in machine learning. Understanding the concepts and operations of linear algebra will enable you to develop, optimize, and troubleshoot machine learning models effectively. LEARNS.EDU.VN is committed to providing you with the resources and guidance you need to master linear algebra and excel in the field of machine learning. Whether you’re a beginner or an experienced practitioner, embracing linear algebra will undoubtedly elevate your skills and career prospects.

Ready to take your machine-learning skills to the next level? Explore the comprehensive resources and courses available at LEARNS.EDU.VN. Whether you’re looking to deepen your understanding of linear algebra or explore other essential topics in machine learning, learns.edu.vn has you covered. Visit us at 123 Education Way, Learnville, CA 90210, United States, or contact us via WhatsApp at +1 555-555-1212. Start your journey today and unlock your full potential in machine learning!

This article provides a comprehensive overview of linear algebra and its applications in machine learning. With a solid understanding of these concepts, you’ll be well-equipped to tackle a wide range of machine learning tasks and stay ahead in this rapidly evolving field.