How Do You Learn Percentages in Math Effectively?

Percentages can seem tricky, but with the right approach, mastering them is achievable. This guide from LEARNS.EDU.VN breaks down learning percentages into simple steps, offering effective strategies and real-world examples. By understanding the basics and practicing regularly, you can confidently tackle percentage problems and apply them in everyday situations, unlocking a new level of mathematical proficiency.

1. What Are Percentages and Why Are They Important?

Percentages are a fundamental concept in mathematics used to express a number as a fraction of 100. The word “percent” comes from the Latin “per centum,” meaning “out of one hundred.” Understanding percentages is crucial because they are widely used in various aspects of daily life, including finance, statistics, and everyday calculations.

Understanding the Definition of Percentages

A percentage is a ratio that compares a number to 100. For example, 50% means 50 out of 100. This concept allows us to express proportions and rates in a standardized manner, making it easier to compare different quantities. According to a study by the National Mathematics Advisory Panel, a solid understanding of fractions and ratios is essential for grasping percentages effectively.

Real-World Applications of Percentages

Percentages are used extensively in:

Finance: Calculating interest rates, discounts, and investment returns.
Retail: Determining sales prices, markups, and profit margins.
Statistics: Presenting data, analyzing trends, and making comparisons.
Everyday Life: Calculating tips, understanding nutritional information, and interpreting survey results.

Why Learning Percentages is Essential

Mastering percentages helps in making informed decisions, understanding financial documents, and solving practical problems. A report by the U.S. Department of Education highlights that individuals with strong numeracy skills, including proficiency in percentages, are more likely to succeed in their careers and manage their finances effectively.

2. What Are the Basic Concepts of Percentages?

Before diving into complex problems, it’s essential to grasp the basic concepts. These include understanding the relationship between percentages, fractions, and decimals, as well as learning how to convert between these forms.

Understanding the Relationship Between Percentages, Fractions, and Decimals

Percentages, fractions, and decimals are different ways of representing the same value. Understanding how they relate to each other is crucial for solving percentage problems.

Percentage to Fraction: A percentage can be written as a fraction with a denominator of 100. For example, 25% is equivalent to 25/100.
Fraction to Percentage: To convert a fraction to a percentage, divide the numerator by the denominator and multiply by 100. For example, 1/4 = (1 ÷ 4) × 100 = 25%.
Percentage to Decimal: To convert a percentage to a decimal, divide by 100. For example, 75% = 75 ÷ 100 = 0.75.
Decimal to Percentage: To convert a decimal to a percentage, multiply by 100. For example, 0.5 = 0.5 × 100 = 50%.

Converting Percentages to Fractions and Decimals

Converting between percentages, fractions, and decimals is a fundamental skill. Here are some examples:

Example 1: Convert 40% to a fraction.

40% = 40/100
Simplify the fraction by dividing both the numerator and denominator by their greatest common divisor, which is 20.
40/100 = 2/5

Example 2: Convert 80% to a decimal.

80% = 80 ÷ 100
80 ÷ 100 = 0.8

Example 3: Convert 0.6 to a percentage.

1. 6 = 0.6 × 100
1. 6 × 100 = 60%

Example 4: Convert 3/4 to a percentage.

3 ÷ 4 = 0.75
1. 75 × 100 = 75%

Common Percentage Conversions

Memorizing common percentage conversions can save time and improve your speed in solving problems. Here’s a table of some common conversions:

Percentage	Fraction	Decimal
10%	1/10	0.1
20%	1/5	0.2
25%	1/4	0.25
33.33%	1/3	0.333
50%	1/2	0.5
66.67%	2/3	0.667
75%	3/4	0.75
100%	1	1.0

Understanding these basic conversions will make more complex percentage calculations easier.

3. What Are the Key Formulas for Solving Percentage Problems?

Knowing the key formulas is essential for solving percentage problems efficiently. These formulas help in finding the percentage of a number, calculating percentage increase or decrease, and determining the original value after a percentage change.

How to Calculate the Percentage of a Number

To find the percentage of a number, use the formula:

Percentage of a number = (Percentage / 100) × Number

Example 1: Find 20% of 500.

(20 / 100) × 500 = 0.2 × 500 = 100

Example 2: What is 35% of 120?

(35 / 100) × 120 = 0.35 × 120 = 42

Calculating Percentage Increase and Decrease

Percentage increase and decrease are used to find the change in a value as a percentage of the original value.

Percentage Increase Formula:

Percentage Increase = [(New Value – Original Value) / Original Value] × 100

Example 1: A price increases from $50 to $60. Calculate the percentage increase.

Percentage Increase = [(60 – 50) / 50] × 100 = (10 / 50) × 100 = 20%

Percentage Decrease Formula:

Percentage Decrease = [(Original Value – New Value) / Original Value] × 100

Example 2: A price decreases from $80 to $60. Calculate the percentage decrease.

Percentage Decrease = [(80 – 60) / 80] × 100 = (20 / 80) × 100 = 25%

Finding the Original Value After a Percentage Change

Sometimes, you need to find the original value after a percentage increase or decrease.

Finding Original Value After Percentage Increase:

Original Value = New Value / (1 + (Percentage Increase / 100))

Example 1: After a 10% increase, the price of an item is $110. Find the original price.

Original Value = 110 / (1 + (10 / 100)) = 110 / 1.1 = $100

Finding Original Value After Percentage Decrease:

Original Value = New Value / (1 – (Percentage Decrease / 100))

Example 2: After a 20% discount, the price of an item is $80. Find the original price.

Original Value = 80 / (1 – (20 / 100)) = 80 / 0.8 = $100

4. What Are Step-by-Step Guides to Solving Percentage Problems?

To effectively solve percentage problems, follow these step-by-step guides with examples. These guides cover finding the percentage of a number, calculating percentage increase and decrease, and finding the original value after a percentage change.

Step-by-Step Guide to Finding the Percentage of a Number

Step 1: Identify the Percentage and the Number

Determine the percentage you need to find and the number you are finding the percentage of.

Step 2: Convert the Percentage to a Decimal

Divide the percentage by 100 to convert it to a decimal.

Step 3: Multiply the Decimal by the Number

Multiply the decimal obtained in Step 2 by the number identified in Step 1.

Example: Find 15% of 200.

Identify the Percentage and the Number: Percentage = 15%, Number = 200
Convert the Percentage to a Decimal: 15% ÷ 100 = 0.15
Multiply the Decimal by the Number: 0.15 × 200 = 30

Therefore, 15% of 200 is 30.

Step-by-Step Guide to Calculating Percentage Increase and Decrease

Step 1: Identify the Original Value and the New Value

Determine the original value and the new value after the change.

Step 2: Calculate the Difference Between the New and Original Values

Subtract the original value from the new value.

Step 3: Divide the Difference by the Original Value

Divide the difference obtained in Step 2 by the original value.

Step 4: Multiply by 100 to Express as a Percentage

Multiply the result from Step 3 by 100 to express the change as a percentage.

Example (Percentage Increase): A price increases from $40 to $50. Calculate the percentage increase.

Identify the Original Value and the New Value: Original Value = $40, New Value = $50
Calculate the Difference Between the New and Original Values: $50 – $40 = $10
Divide the Difference by the Original Value: $10 ÷ $40 = 0.25
Multiply by 100 to Express as a Percentage: 0.25 × 100 = 25%

Therefore, the percentage increase is 25%.

Example (Percentage Decrease): A price decreases from $100 to $70. Calculate the percentage decrease.

Identify the Original Value and the New Value: Original Value = $100, New Value = $70
Calculate the Difference Between the New and Original Values: $100 – $70 = $30
Divide the Difference by the Original Value: $30 ÷ $100 = 0.30
Multiply by 100 to Express as a Percentage: 0.30 × 100 = 30%

Therefore, the percentage decrease is 30%.

Step-by-Step Guide to Finding the Original Value After a Percentage Change

Step 1: Identify the New Value and the Percentage Change

Determine the new value after the percentage change and the percentage change itself.

Step 2: Determine Whether It’s an Increase or Decrease

Identify whether the percentage change is an increase or a decrease.

Step 3: Apply the Appropriate Formula

If it’s an increase, use the formula: Original Value = New Value / (1 + (Percentage Increase / 100))
If it’s a decrease, use the formula: Original Value = New Value / (1 – (Percentage Decrease / 100))

Example (After Percentage Increase): After a 20% increase, the price of an item is $60. Find the original price.

Identify the New Value and the Percentage Change: New Value = $60, Percentage Increase = 20%
Determine Whether It’s an Increase or Decrease: Increase
Apply the Appropriate Formula: Original Value = 60 / (1 + (20 / 100)) = 60 / 1.2 = $50

Therefore, the original price was $50.

Example (After Percentage Decrease): After a 25% discount, the price of an item is $75. Find the original price.

Identify the New Value and the Percentage Change: New Value = $75, Percentage Decrease = 25%
Determine Whether It’s an Increase or Decrease: Decrease
Apply the Appropriate Formula: Original Value = 75 / (1 – (25 / 100)) = 75 / 0.75 = $100

Therefore, the original price was $100.

By following these step-by-step guides and practicing regularly, you can improve your skills in solving percentage problems.

5. What Are Some Common Mistakes to Avoid When Working With Percentages?

Working with percentages can be tricky, and it’s easy to make mistakes if you’re not careful. Here are some common mistakes to avoid, along with explanations and examples to help you understand why they are incorrect.

Misunderstanding the Base Value

One of the most common mistakes is misunderstanding the base value to which the percentage is applied. Always ensure you know which number represents 100% before calculating percentages.

Incorrect Example: A store offers a 20% discount on an item originally priced at $100. Later, they offer an additional 10% discount. A customer thinks the total discount is 30%.

Why It’s Incorrect: The second discount is applied to the discounted price, not the original price.
Correct Calculation:
- First discount: 20% of $100 = $20, so the price becomes $80.
- Second discount: 10% of $80 = $8, so the final price is $72.
- Total discount: $100 – $72 = $28, which is 28% of the original price, not 30%.

Incorrectly Converting Percentages to Decimals or Fractions

Another common mistake is incorrectly converting percentages to decimals or fractions. This can lead to significant errors in calculations.

Incorrect Example: Calculating 5% of 200 by using 0.5 as the decimal equivalent of 5%.

Why It’s Incorrect: 5% as a decimal is 0.05, not 0.5.
Correct Calculation:
- 5% = 5 / 100 = 0.05
- 1. 05 × 200 = 10

Adding or Subtracting Percentages Incorrectly

Percentages cannot be directly added or subtracted unless they are percentages of the same base value.

Incorrect Example: A company’s revenue increased by 10% in the first year and 15% in the second year. Someone claims the total increase is 25%.

Why It’s Incorrect: The 15% increase in the second year is based on the increased revenue from the first year, not the original revenue.
Correct Calculation:
- Let’s assume the initial revenue is $100.
- After the first year: $100 + (10% of $100) = $110
- After the second year: $110 + (15% of $110) = $110 + $16.50 = $126.50
- Total increase: $126.50 – $100 = $26.50, which is 26.5%, not 25%.

Forgetting to Divide by 100 When Converting to a Decimal

When converting a percentage to a decimal for calculation purposes, it is essential to divide by 100.

Incorrect Example: Calculating 30% of 400 by multiplying 30 × 400 without converting 30% to a decimal.

Why It’s Incorrect: The percentage must be converted to a decimal before multiplying.
Correct Calculation:
- 30% = 30 / 100 = 0.3
- 1. 3 × 400 = 120

Confusing Percentage Increase and Percentage Decrease

Confusing the formulas for percentage increase and decrease can lead to incorrect results.

Incorrect Example: Calculating the percentage decrease when the value actually increased.

Why It’s Incorrect: Using the wrong formula will give you a percentage change in the wrong direction.
Correct Calculation:
- If a value changes from 100 to 120, it’s an increase.
- Percentage Increase = [(120 – 100) / 100] × 100 = 20%
- If you mistakenly use the decrease formula, you’ll get a negative value, indicating an incorrect calculation.

Ignoring the Context of the Problem

Sometimes, the context of the problem can change how you should approach the calculation. Always read the problem carefully to understand what is being asked.

Incorrect Example: A store marks up an item by 50% and then offers a 50% discount. A customer thinks the final price is the same as the original price.

Why It’s Incorrect: The markup and discount are applied to different base values.
Correct Calculation:
- Let’s assume the original price is $100.
- Markup: $100 + (50% of $100) = $150
- Discount: $150 – (50% of $150) = $150 – $75 = $75
- The final price is $75, which is not the same as the original price.

Using Percentages Without Proper Units

Always include the units (e.g., %, $, kg) when stating percentages to avoid confusion.

Incorrect Example: Saying “The increase is 20” without specifying 20%.

Why It’s Incorrect: It’s unclear whether the increase is 20%, 20 dollars, or some other unit.
Correct Usage: “The increase is 20%.”

By avoiding these common mistakes, you can improve your accuracy and confidence when working with percentages.

6. What Are Tips and Tricks for Mastering Percentages?

Mastering percentages requires practice and a good understanding of underlying concepts. Here are some effective tips and tricks to help you improve your skills and solve percentage problems more efficiently.

Practice Regularly with Real-World Problems

Consistent practice is key to mastering any mathematical concept. Solve a variety of percentage problems from different contexts to reinforce your understanding.

Real-World Examples:
- Shopping: Calculate discounts, sales tax, and total costs.
- Finance: Determine interest on loans, investment returns, and budget allocations.
- Cooking: Adjust ingredient quantities based on percentages.
- Health: Understand nutritional information and calculate daily nutrient intake.

Use Visual Aids and Diagrams

Visual aids such as diagrams, charts, and graphs can help you understand percentage relationships more clearly.

Bar Graphs: Use bar graphs to compare different percentages.
Pie Charts: Use pie charts to show how a whole is divided into percentages.
Number Lines: Use number lines to visualize percentage increase and decrease.

Memorize Common Percentage Equivalents

Memorizing common percentage equivalents can save time and improve your speed in solving problems.

Percentage	Fraction	Decimal
1%	1/100	0.01
5%	1/20	0.05
10%	1/10	0.1
20%	1/5	0.2
25%	1/4	0.25
33.33%	1/3	0.333
50%	1/2	0.5
66.67%	2/3	0.667
75%	3/4	0.75
100%	1	1.0

Break Down Complex Problems Into Simpler Steps

Complex percentage problems can be overwhelming. Break them down into smaller, more manageable steps to make them easier to solve.

Example: A store offers a 30% discount on an item, and then an additional 15% off the discounted price. If the original price is $200, what is the final price?

Calculate the first discount: 30% of $200 = 0.3 × $200 = $60
Subtract the first discount from the original price: $200 – $60 = $140
Calculate the second discount: 15% of $140 = 0.15 × $140 = $21
Subtract the second discount from the discounted price: $140 – $21 = $119

Therefore, the final price is $119.

Estimate and Check Your Answers

Before solving a percentage problem, estimate the answer to get a rough idea of what the result should be. After solving the problem, check your answer to ensure it is reasonable.

Example: Estimate 25% of 80.

Estimation: 25% is the same as 1/4, so 1/4 of 80 is around 20.
Calculation: 25% of 80 = 0.25 × 80 = 20
Check: The calculated answer matches the estimation, so it is likely correct.

Understand the Language of Percentage Problems

Pay attention to the language used in percentage problems. Key words and phrases can provide clues about how to solve the problem.

“Of” means multiply.
“Is” means equals.
“What percent” means find the percentage.
“Increase/Decrease” indicates percentage change.

Use Technology and Online Resources

Take advantage of technology and online resources to practice and improve your percentage skills.

Calculators: Use calculators to perform complex calculations quickly.
Online Tutorials: Watch online tutorials to learn different methods for solving percentage problems.
Practice Websites: Use practice websites to solve a variety of percentage problems and track your progress.

Teach Someone Else

One of the best ways to reinforce your understanding of percentages is to teach someone else. Explaining the concepts to others will help you identify any gaps in your knowledge and solidify your understanding.

Apply Percentages in Daily Life

Look for opportunities to apply percentages in your daily life. This will help you see the practical relevance of percentages and make learning them more engaging.

Calculate tips at restaurants.
Determine the sale price of items at the store.
Calculate the interest on your savings account.
Track your progress towards a fitness goal.

By following these tips and tricks, you can enhance your understanding of percentages and improve your ability to solve percentage problems efficiently and accurately.

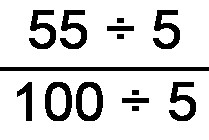Convert percentage to decimal

7. What Are the Advanced Percentage Applications?

Beyond the basics, percentages have advanced applications in various fields. Understanding these applications can help you appreciate the versatility and importance of percentages in real-world scenarios.

Compound Interest

Compound interest is the interest calculated on the initial principal, which also includes all of the accumulated interest from previous periods. It’s a powerful concept in finance and investment.

Formula for Compound Interest:

A = P (1 + r/n)^(nt)

Where:

A = the future value of the investment/loan, including interest
P = the principal investment amount (the initial deposit or loan amount)
r = the annual interest rate (as a decimal)
n = the number of times that interest is compounded per year
t = the number of years the money is invested or borrowed for

Example: If you invest $1,000 at an annual interest rate of 5% compounded annually for 10 years, what will be the future value of your investment?

P = $1,000
r = 0.05
n = 1
t = 10

A = 1000 (1 + 0.05/1)^(1*10) = 1000 (1.05)^10 = $1,628.89

Statistical Analysis

Percentages are widely used in statistical analysis to present data, analyze trends, and make comparisons.

Data Representation: Percentages are used to represent proportions in datasets, such as the percentage of respondents who agree with a particular statement.
Trend Analysis: Percentages are used to track changes in data over time, such as the percentage increase in sales from one year to the next.
Comparative Analysis: Percentages are used to compare different groups or categories, such as the percentage of males versus females in a survey.

Example: In a survey, 60% of respondents agreed with a particular statement, 25% disagreed, and 15% were neutral. These percentages provide a clear picture of the distribution of opinions.

Business and Finance

Percentages are essential in business and finance for calculating profit margins, growth rates, and financial ratios.

Profit Margin: The percentage of revenue that remains after deducting all expenses.
Growth Rate: The percentage increase in revenue, sales, or other metrics over a period of time.
Financial Ratios: Ratios expressed as percentages to assess a company’s financial performance and stability.

Example: A company has a revenue of $500,000 and expenses of $300,000. The profit margin is calculated as:

Profit = Revenue – Expenses = $500,000 – $300,000 = $200,000
Profit Margin = (Profit / Revenue) × 100 = ($200,000 / $500,000) × 100 = 40%

Scientific Research

Percentages are used in scientific research to express experimental results, analyze data, and compare different groups.

Experimental Results: Percentages are used to express the success rate of an experiment, such as the percentage of patients who responded to a treatment.
Data Analysis: Percentages are used to analyze the distribution of data in a sample, such as the percentage of individuals with a particular characteristic.
Comparative Studies: Percentages are used to compare the outcomes of different treatments or interventions.

Example: In a clinical trial, 75% of patients who received a new drug showed improvement, compared to 50% of patients who received a placebo.

Everyday Life

Percentages are used in numerous everyday situations, from calculating tips and discounts to understanding statistics and making informed decisions.

Tips and Discounts: Calculating tips at restaurants and discounts at stores.
Statistics: Understanding statistics presented in the news or in reports.
Decision Making: Making informed decisions about financial investments, health, and other aspects of life.

Example: When dining at a restaurant, calculating a 15% tip on a bill of $40:

Tip = 15% of $40 = 0.15 × $40 = $6

Understanding these advanced applications of percentages can help you appreciate their versatility and importance in various fields.

8. How Can LEARNS.EDU.VN Help You Master Percentages?

LEARNS.EDU.VN offers a wide range of resources and tools to help you master percentages and improve your mathematical skills. From detailed lessons and practice exercises to personalized support and expert guidance, LEARNS.EDU.VN provides everything you need to succeed.

Comprehensive Lessons and Tutorials

LEARNS.EDU.VN provides comprehensive lessons and tutorials that cover all aspects of percentages, from basic concepts to advanced applications.

Step-by-Step Guides: Clear, step-by-step guides that explain how to solve different types of percentage problems.
Video Tutorials: Engaging video tutorials that demonstrate how to apply percentage concepts in real-world scenarios.
Detailed Explanations: Thorough explanations of the underlying principles and formulas related to percentages.

Practice Exercises and Quizzes

LEARNS.EDU.VN offers a variety of practice exercises and quizzes to help you reinforce your understanding and improve your skills.

Interactive Exercises: Interactive exercises that provide immediate feedback and help you identify areas where you need to improve.
Quizzes: Quizzes that test your knowledge and assess your progress.
Progress Tracking: Tools that track your performance and provide insights into your strengths and weaknesses.

Personalized Learning Paths

LEARNS.EDU.VN offers personalized learning paths that adapt to your individual needs and learning style.

Adaptive Learning: Adaptive learning technology that adjusts the difficulty of the material based on your performance.
Customized Recommendations: Customized recommendations for lessons, exercises, and resources based on your goals and interests.
Flexible Scheduling: Flexible scheduling options that allow you to learn at your own pace and on your own schedule.

Expert Support and Guidance

LEARNS.EDU.VN provides access to expert support and guidance from experienced educators and mathematicians.

Live Q&A Sessions: Live Q&A sessions with experts who can answer your questions and provide personalized assistance.
Online Forums: Online forums where you can connect with other learners and share tips and insights.
Email Support: Email support for technical issues and academic inquiries.

Real-World Applications and Examples

LEARNS.EDU.VN emphasizes the real-world applications of percentages, providing examples and case studies from various fields.

Financial Planning: Examples of how percentages are used in financial planning, such as calculating investment returns and managing budgets.
Business Analysis: Examples of how percentages are used in business analysis, such as calculating profit margins and analyzing market trends.
Scientific Research: Examples of how percentages are used in scientific research, such as analyzing experimental data and interpreting results.

Mobile Accessibility

LEARNS.EDU.VN is accessible on mobile devices, allowing you to learn and practice percentages anytime, anywhere.

Mobile-Friendly Website: A mobile-friendly website that is optimized for viewing on smartphones and tablets.
Mobile Apps: Dedicated mobile apps for iOS and Android devices that provide a seamless learning experience.

Community and Collaboration

LEARNS.EDU.VN fosters a community of learners who can support each other and collaborate on projects.

Discussion Boards: Discussion boards where you can ask questions, share ideas, and collaborate with other learners.
Group Projects: Opportunities to participate in group projects and work with others to solve complex percentage problems.
Peer Review: Peer review activities that allow you to provide feedback on the work of others and receive feedback on your own work.

Success Stories and Testimonials

LEARNS.EDU.VN features success stories and testimonials from learners who have successfully mastered percentages using our resources.

Inspiring Stories: Inspiring stories that demonstrate the impact of LEARNS.EDU.VN on learners’ lives.
Positive Testimonials: Positive testimonials that highlight the effectiveness of our resources and the quality of our support.

By leveraging the resources and tools available at learns.edu.vn, you can master percentages and unlock new opportunities in your personal and professional life.

9. What Are the Common Percentage Scenarios and Examples?

Understanding common percentage scenarios and working through examples can help you apply your knowledge in practical situations. Here are some common scenarios and examples to illustrate how percentages are used in everyday life.

Calculating Discounts

Discounts are a common application of percentages in retail and shopping.

Example: A store offers a 25% discount on an item originally priced at $80. What is the sale price?

Calculate the discount amount: 25% of $80 = 0.25 × $80 = $20
Subtract the discount from the original price: $80 – $20 = $60

Therefore, the sale price is $60.

Calculating Sales Tax

Sales tax is a percentage of the purchase price that is added to the total cost.

Example: The sales tax rate is 8%, and you purchase an item for $50. What is the total cost, including sales tax?

Calculate the sales tax amount: 8% of $50 = 0.08 × $50 = $4
Add the sales tax to the purchase price: $50 + $4 = $54

Therefore, the total cost is $54.

Calculating Tips

Tipping is a common practice in restaurants and other service industries, where a percentage of the bill is added as a gratuity.

Example: You want to leave a 15% tip on a restaurant bill of $35. How much should you tip?

Calculate the tip amount: 15% of $35 = 0.15 × $35 = $5.25

Therefore, you should tip $5.25.

Calculating Interest

Interest is a percentage of the principal amount that is earned on savings or paid on loans.

Example: You deposit $1,000 in a savings account that earns 2% annual interest. How much interest will you earn in one year?

Calculate the interest amount: 2% of $1,000 = 0.02 × $1,000 = $20

Therefore, you will earn $20 in interest.

Analyzing Survey Results

Percentages are often used to present the results of surveys and polls.

Example: In a survey, 60% of respondents said they prefer coffee over tea. If 500 people were surveyed, how many prefer coffee?

Calculate the number of people who prefer coffee: 60% of 500 = 0.6 × 500 = 300

Therefore, 300 people prefer coffee.

Calculating Percentage Change

Percentage change is used to measure the increase or decrease in a value over time.

Example: A company’s revenue increased from $200,000 to $250,000. What is the percentage increase?

Calculate the difference between the new and original values: $250,000 – $200,000 = $50,000
Divide the difference by the original value: $50,000 / $200,000 = 0.25
Multiply by 100 to express as a percentage: 0.25 × 100 = 25%