How To Learn Divide In Math: A Comprehensive Guide

Learning How To Learn Divide In Math can be challenging, but with the right approach, it becomes manageable. At LEARNS.EDU.VN, we offer clear, step-by-step guidance and resources to simplify division. Our educational platform provides the tools and support needed to grasp division concepts, transforming it from a daunting task into an achievable skill, fostering a deeper understanding of mathematics, arithmetic operations and numerical problem-solving.

1. Understanding the Basics of Division

Division is a fundamental arithmetic operation that involves splitting a whole into equal parts. Mastering division is crucial for progressing in mathematics and in everyday problem-solving.

1.1. What is Division?

Division is the inverse operation of multiplication. It determines how many times one number (the divisor) is contained within another number (the dividend). The result of division is called the quotient. Understanding this relationship is key to grasping division.

Basic Components of Division:

• Dividend: The number being divided.
• Divisor: The number by which the dividend is divided.
• Quotient: The result of the division.
• Remainder: The amount left over when the dividend cannot be evenly divided by the divisor.

1.2. Key Terminology for Division

Familiarizing yourself with the terminology used in division is crucial for understanding and solving division problems effectively. Here’s a breakdown of essential terms:

Term	Definition	Example
Dividend	The number being divided.	In 10 ÷ 2 = 5, 10 is the dividend.
Divisor	The number that divides the dividend.	In 10 ÷ 2 = 5, 2 is the divisor.
Quotient	The result of the division.	In 10 ÷ 2 = 5, 5 is the quotient.
Remainder	The amount left over when the dividend cannot be evenly divided by the divisor.	In 11 ÷ 2 = 5 R1, 1 is the remainder.
Division Symbol	The symbol used to denote division (÷).	10 ÷ 2

1.3. Real-World Applications of Division

Division isn’t just a math concept; it’s a skill used daily. From splitting a bill among friends to calculating how many items can be bought with a certain amount of money, division is essential. Consider these examples:

• Sharing Costs: If a group of 5 friends has a restaurant bill of $50, they use division (50 ÷ 5) to determine each person’s share, which is $10.
• Cooking: A recipe calls for 2 cups of flour to make 12 cookies. To make 36 cookies, you need to divide 36 by 12 to find that you need to triple the recipe. Therefore, you’ll need 6 cups of flour.
• Travel Planning: A family driving 300 miles wants to know how long the trip will take at 60 miles per hour. They divide the total distance by the speed (300 ÷ 60) to find the trip will take 5 hours.

Understanding these applications helps contextualize division and makes it more relatable.

2. Foundational Concepts to Master Before Division

Before diving into division, ensure a solid grasp of prerequisite math skills. These foundational concepts will make learning division smoother and more intuitive.

2.1. Understanding Multiplication

Since division is the inverse of multiplication, a strong understanding of multiplication is crucial. Knowing multiplication facts helps in quickly determining quotients.

Why Multiplication Matters for Division:

• Inverse Relationship: Division problems can be solved by thinking of the related multiplication fact. For example, to solve 20 ÷ 4, think: “What number times 4 equals 20?”
• Fact Families: Understanding fact families (e.g., 3 x 4 = 12, 4 x 3 = 12, 12 ÷ 3 = 4, 12 ÷ 4 = 3) reinforces the relationship between multiplication and division.

How to Improve Multiplication Skills:

• Multiplication Tables: Memorize multiplication tables up to 12×12. Use flashcards, online games, or apps to make it engaging.
• Practice: Regularly practice multiplication problems. Start with simple facts and gradually increase complexity.
• Real-World Examples: Relate multiplication to everyday scenarios, like calculating the total cost of multiple items or determining the number of seats in rows of chairs.

2.2. Grasping Subtraction

Subtraction is another essential operation for division, especially when using methods like long division. Being able to subtract accurately and efficiently is key.

Why Subtraction is Important in Division:

• Long Division: In long division, subtraction is used to find the remainder after each step of dividing.
• Repeated Subtraction: Understanding division as repeated subtraction can simplify the concept. For example, 15 ÷ 3 can be thought of as subtracting 3 from 15 repeatedly until you reach zero (15 – 3 – 3 – 3 – 3 – 3 = 0).

Ways to Enhance Subtraction Skills:

• Mental Math: Practice mental subtraction with different numbers. Start with small numbers and gradually increase difficulty.
• Worksheets and Exercises: Use subtraction worksheets and exercises to reinforce skills. Focus on accuracy and speed.
• Real-Life Scenarios: Apply subtraction to real-world situations, such as calculating change when making a purchase or determining the difference between two quantities.

2.3. Familiarity with Number Patterns

Recognizing number patterns can significantly aid in understanding and solving division problems. Patterns help in estimating and checking the reasonableness of answers.

How Number Patterns Help in Division:

• Divisibility Rules: Understanding divisibility rules (e.g., a number is divisible by 2 if it’s even, by 5 if it ends in 0 or 5, by 10 if it ends in 0) makes division quicker.
• Estimation: Patterns help estimate quotients. For example, knowing that 45 is close to 50 helps estimate 450 ÷ 9.

Tips for Recognizing Number Patterns:

• Practice with Multiples: Regularly work with multiples of different numbers to identify patterns.
• Divisibility Rule Exercises: Practice applying divisibility rules to various numbers.
• Pattern Recognition Games: Use games and puzzles that involve identifying number patterns to make learning fun.

3. Division Methods: A Step-by-Step Guide

There are several methods to approach division, each with its own advantages. Understanding these methods provides a versatile toolkit for solving division problems.

3.1. Division Using Arrays

Arrays are visual representations that organize numbers into rows and columns. This method is excellent for introducing division conceptually, especially for visual learners.

How to Use Arrays for Division:

1. Represent the Dividend: Draw a grid representing the total number (dividend) you are dividing.
2. Form Equal Rows: Arrange the grid into equal rows based on the divisor.
3. Count Columns: The number of columns in each row represents the quotient.

Example:

Solve 12 ÷ 3 using an array.

• Draw a grid of 12 squares.
• Arrange the squares into 3 equal rows.
• Each row has 4 squares, so 12 ÷ 3 = 4.

Arrays help visualize how division involves splitting a total into equal groups.

3.2. Area Model Division

The area model, similar to arrays, uses a rectangular model to visualize division. It’s particularly useful for dividing larger numbers.

How to Use the Area Model for Division:

1. Draw a Rectangle: Draw a rectangle representing the dividend (total area).
2. Divide the Rectangle: Divide the rectangle into sections based on the divisor.
3. Find the Length: Determine the length of each section to find the quotient.

Example:

Solve 48 ÷ 4 using an area model.

• Draw a rectangle representing 48.
• Divide it into 4 equal sections (width = 4).
• Determine the length of each section (length = 12), so 48 ÷ 4 = 12.

The area model helps break down larger division problems into smaller, more manageable parts.

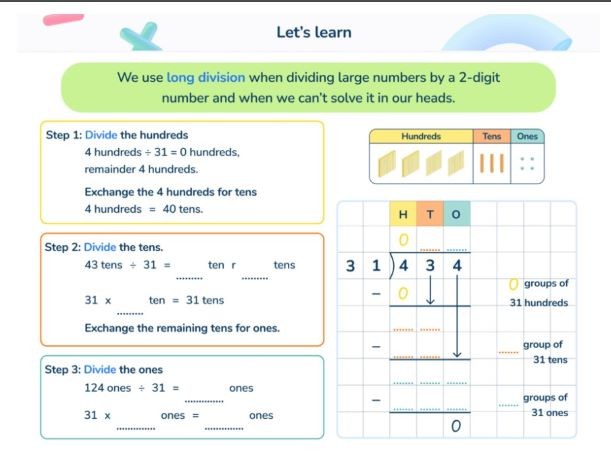
3.3. Long Division

Long division is a standard algorithm used for dividing larger numbers. It requires a systematic approach involving division, multiplication, subtraction, and bringing down numbers.

Steps for Long Division:

1. Set Up the Problem: Write the dividend inside the division symbol and the divisor outside.
2. Divide: Divide the first digit(s) of the dividend by the divisor.
3. Multiply: Multiply the quotient by the divisor.
4. Subtract: Subtract the result from the corresponding part of the dividend.
5. Bring Down: Bring down the next digit of the dividend.
6. Repeat: Repeat steps 2-5 until all digits of the dividend have been used.

Example:

Solve 528 ÷ 24 using long division.

• Set up:

     ______
  24 | 528

• Divide: 24 goes into 52 two times (2 x 24 = 48).

     2____
  24 | 528
     48

• Subtract: 52 – 48 = 4.

     2____
  24 | 528
     48
     ---
      4

• Bring Down: Bring down the 8.

     2____
  24 | 528
     48
     ---
      48

• Divide: 24 goes into 48 two times (2 x 24 = 48).

     22___
  24 | 528
     48
     ---
      48
      48

• Subtract: 48 – 48 = 0.

     22___
  24 | 528
     48
     ---
      48
      48
     ---
      0

Therefore, 528 ÷ 24 = 22.

Long division is essential for tackling complex division problems, and mastering it provides a solid foundation for more advanced math.

4. Handling Remainders in Division

In many division problems, the dividend is not perfectly divisible by the divisor, resulting in a remainder. Understanding how to interpret and work with remainders is essential.

4.1. What are Remainders?

A remainder is the amount left over after performing division when the dividend cannot be divided evenly by the divisor. It represents the portion that does not fit into a whole number of groups.

How to Identify Remainders:

• Perform the division.
• If the divisor does not divide evenly into the dividend, the leftover amount is the remainder.

Example:

Solve 25 ÷ 4.

• 4 goes into 25 six times (6 x 4 = 24).
• The remainder is 25 – 24 = 1.

Therefore, 25 ÷ 4 = 6 R1 (6 with a remainder of 1).

4.2. Interpreting Remainders in Real-World Contexts

Remainders take on different meanings depending on the context of the problem. It’s important to interpret them appropriately to answer the question accurately.

Different Interpretations of Remainders:

• Leftover Amount: Sometimes, the remainder is simply the leftover amount that cannot be divided further.
• Rounding Up: In some cases, the remainder necessitates rounding up to the next whole number.
• Fraction or Decimal: The remainder can be expressed as a fraction or decimal to provide a more precise answer.

Examples:

• Sharing Items: If you have 25 cookies and want to share them equally among 4 friends, each friend gets 6 cookies, and there is 1 cookie left over.
• Transportation: If you need to transport 25 people in vans that hold 4 people each, you need 7 vans because the remainder of 1 person requires an additional van.
• Calculating Costs: If an item costs $4 and you have $25, you can buy 6 items, and you’ll have $1 left over.

4.3. Converting Remainders to Fractions or Decimals

To express a remainder as a fraction or decimal, follow these steps:

Converting to a Fraction:

1. Write the Remainder: Write the remainder as the numerator of the fraction.
2. Use the Divisor: Use the divisor as the denominator of the fraction.

Example:

Express the remainder of 25 ÷ 4 as a fraction.

• The remainder is 1, and the divisor is 4.
• The fraction is 1/4.

Therefore, 25 ÷ 4 = 6 1/4.

Converting to a Decimal:

1. Add a Decimal and Zero: Add a decimal point and a zero to the dividend.
2. Continue Dividing: Continue the long division process.
3. Round if Necessary: Round the decimal to the desired place value.

Example:

Express the remainder of 25 ÷ 4 as a decimal.

• Add .0 to 25, making it 25.0.
• Continue dividing:

     6.25
  4 | 25.00
     24
     ---
      1 0
        8
      ---
        20
        20
       ---
         0

Therefore, 25 ÷ 4 = 6.25.

5. Division with Multi-Digit Numbers

Dividing with multi-digit numbers can seem daunting, but with a systematic approach and understanding of place value, it becomes manageable.

5.1. Understanding Place Value

A solid grasp of place value is essential for dividing multi-digit numbers. Knowing the value of each digit (ones, tens, hundreds, etc.) helps in organizing and solving the problem.

Importance of Place Value:

• Organizing Numbers: Place value helps keep track of each digit’s value during the division process.
• Correct Placement of Digits: Understanding place value ensures digits are placed correctly in the quotient.

Example:

In the number 345:

• 3 is in the hundreds place (300).
• 4 is in the tens place (40).
• 5 is in the ones place (5).

5.2. Step-by-Step Guide to Dividing Multi-Digit Numbers

Follow these steps to divide multi-digit numbers effectively:

1. Set Up the Problem: Write the dividend and divisor in the long division format.
2. Divide: Divide the first digit(s) of the dividend by the divisor.
3. Multiply: Multiply the quotient by the divisor.
4. Subtract: Subtract the result from the corresponding part of the dividend.
5. Bring Down: Bring down the next digit of the dividend.
6. Repeat: Repeat steps 2-5 until all digits of the dividend have been used.

Example:

Solve 1,236 ÷ 12.

• Set up:

       ______
  12 | 1236

• Divide: 12 goes into 12 one time (1 x 12 = 12).

       1___
  12 | 1236
       12

• Subtract: 12 – 12 = 0.

       1___
  12 | 1236
       12
       ---
        0

• Bring Down: Bring down the 3.

       1___
  12 | 1236
       12
       ---
        03

• Divide: 12 goes into 3 zero times (0 x 12 = 0).

       10__
  12 | 1236
       12
       ---
        03
        0

• Subtract: 3 – 0 = 3.

       10__
  12 | 1236
       12
       ---
        03
        0
       ---
        3

• Bring Down: Bring down the 6.

       10__
  12 | 1236
       12
       ---
        036
        0
       ---
        36

• Divide: 12 goes into 36 three times (3 x 12 = 36).

       103_
  12 | 1236
       12
       ---
        036
        0
       ---
        36
        36

• Subtract: 36 – 36 = 0.

       103_
  12 | 1236
       12
       ---
        036
        0
       ---
        36
        36
       ---
         0

Therefore, 1,236 ÷ 12 = 103.

5.3. Tips for Simplifying Multi-Digit Division

• Estimate: Estimate the quotient before starting to ensure the answer is reasonable.
• Break Down the Problem: Break the dividend into smaller parts to make the division process easier.
• Use Multiplication Facts: Knowing multiplication facts speeds up the division process.
• Practice Regularly: Consistent practice builds confidence and fluency.

6. Dividing Decimals

Dividing decimals involves understanding place value and applying similar techniques used in whole number division.

6.1. Basic Rules for Dividing Decimals

1. Set Up the Problem: Write the dividend and divisor.
2. Make the Divisor a Whole Number: Move the decimal point in the divisor to the right until it becomes a whole number.
3. Move Decimal in Dividend: Move the decimal point in the dividend the same number of places to the right.
4. Divide: Perform the division as with whole numbers.
5. Place Decimal in Quotient: Place the decimal point in the quotient directly above the decimal point in the dividend.

6.2. Dividing a Decimal by a Whole Number

Example:

Solve 4.2 ÷ 2.

• Set up:

     ______
  2 | 4.2

• Divide: Divide as with whole numbers, placing the decimal point in the quotient above the decimal point in the dividend.

     2.1
  2 | 4.2
     4
     ---
      02
      2
     ---
      0

Therefore, 4.2 ÷ 2 = 2.1.

6.3. Dividing a Decimal by a Decimal

Example:

Solve 1.44 ÷ 1.2.

• Set up:

       ______
  1.2 | 1.44

• Make Divisor a Whole Number: Move the decimal point one place to the right in both the divisor and dividend.

       ______
  12 | 14.4

• Divide: Divide as with whole numbers.

       1.2
  12 | 14.4
       12
       ---
        24
        24
       ---
        0

Therefore, 1.44 ÷ 1.2 = 1.2.

7. Common Mistakes to Avoid When Dividing

Avoiding common mistakes is crucial for mastering division. Here are some pitfalls to watch out for:

7.1. Misunderstanding Place Value

• Mistake: Incorrectly placing digits in the quotient.
• Solution: Double-check the placement of digits and ensure each digit’s value is accounted for.

7.2. Forgetting to Bring Down Digits

• Mistake: Skipping a digit in the dividend.
• Solution: Systematically bring down each digit, even if the divisor does not divide into it.

7.3. Incorrect Subtraction

• Mistake: Making errors in subtraction during long division.
• Solution: Double-check each subtraction step and ensure accuracy.

7.4. Not Accounting for Zeroes in the Quotient

• Mistake: Omitting zeroes when the divisor does not divide into a portion of the dividend.
• Solution: Include a zero in the quotient when the divisor is larger than the current part of the dividend.

8. Practice Problems and Exercises

Practice is key to mastering division. Here are some problems to test your skills:

8.1. Basic Division Problems

1. 36 ÷ 6 = ?
2. 48 ÷ 8 = ?
3. 63 ÷ 9 = ?
4. 24 ÷ 4 = ?
5. 56 ÷ 7 = ?

8.2. Multi-Digit Division Problems

1. 432 ÷ 12 = ?
2. 625 ÷ 25 = ?
3. 1,296 ÷ 36 = ?
4. 2,048 ÷ 64 = ?
5. 3,125 ÷ 125 = ?

8.3. Decimal Division Problems

1. 6.4 ÷ 2 = ?
2. 14.4 ÷ 1.2 = ?
3. 25.5 ÷ 2.5 = ?
4. 1.69 ÷ 1.3 = ?
5. 0.81 ÷ 0.9 = ?

8.4. Word Problems Involving Division

1. A baker makes 72 cookies and wants to put them into boxes of 6. How many boxes does she need?
2. A school has 360 students and wants to divide them into 12 equal groups. How many students are in each group?
3. A runner runs 26.2 miles in 4 hours. What is her average speed per hour?
4. A store sells apples for $0.75 each. How many apples can you buy with $15?
5. A group of friends has a dinner bill of $120 and wants to split it evenly among 8 people. How much does each person owe?

9. Resources for Further Learning

To deepen your understanding of division, here are some valuable resources:

9.1. Online Educational Platforms

• LEARNS.EDU.VN: Offers comprehensive math courses and personalized learning paths.
• Khan Academy: Provides free video lessons and practice exercises covering various math topics.
• Mathway: A problem-solving tool that offers step-by-step solutions.

9.2. Math Textbooks and Workbooks

• Saxon Math: Known for its incremental approach to learning math concepts.
• Singapore Math: Emphasizes problem-solving and conceptual understanding.
• Practice Workbooks: Many publishers offer workbooks with division exercises and problems.

9.3. Educational Apps and Games

• Prodigy Math Game: An engaging game that reinforces math skills.
• DragonBox Numbers: Helps build number sense and understanding of arithmetic operations.
• SplashLearn: Offers interactive math games and exercises.

10. Frequently Asked Questions (FAQs) About Learning Division

Here are some common questions about learning division, along with detailed answers to help clarify any confusion:

10.1. What is the best way to learn division for beginners?

For beginners, starting with visual aids like arrays and area models can make the concept of division more concrete. Use real-world examples and relate division to sharing or grouping items.

10.2. How can I help my child with division homework?

Provide a quiet study environment, review the basic concepts, and work through example problems together. Encourage your child to explain their thought process and offer assistance without giving direct answers.

10.3. What are some effective strategies for memorizing division facts?

Use flashcards, online games, and mnemonics to memorize division facts. Practice regularly and relate division facts to multiplication facts.

10.4. How do I explain remainders to a child?

Explain that a remainder is the amount left over when you can’t divide evenly. Use examples like sharing cookies or grouping toys to illustrate the concept.

10.5. What is long division, and how is it different from other methods?

Long division is a standard algorithm used for dividing larger numbers. It involves a systematic process of dividing, multiplying, subtracting, and bringing down digits. Unlike arrays or area models, it is more efficient for complex division problems.

10.6. How do I divide decimals?

To divide decimals, make the divisor a whole number by moving the decimal point. Move the decimal point in the dividend the same number of places. Then, perform the division as with whole numbers, placing the decimal point in the quotient directly above the decimal point in the dividend.

10.7. What should I do if I keep making mistakes in division?

Identify the types of mistakes you are making and practice those specific areas. Review the basic concepts and seek help from a teacher, tutor, or online resources.

10.8. Can division problems always be solved with a whole number answer?

No, division problems can result in remainders, fractions, or decimals. The type of answer depends on the numbers being divided and the context of the problem.

10.9. What are some real-world applications of division?

Division is used in various real-world scenarios, such as sharing costs, cooking, travel planning, and calculating measurements.

10.10. How does LEARNS.EDU.VN help with learning division?

LEARNS.EDU.VN provides structured courses, personalized learning paths, and comprehensive resources to help learners master division. Our platform offers step-by-step guidance, practice exercises, and expert support to ensure a thorough understanding of division concepts.

Learning division in math is a journey that requires patience, practice, and the right resources. By understanding the basic concepts, mastering different division methods, and avoiding common mistakes, you can build a strong foundation in division. Remember to use real-world examples, seek help when needed, and practice consistently to improve your skills.

Ready to take your division skills to the next level? Visit LEARNS.EDU.VN today and explore our comprehensive math courses and resources. Whether you’re a student, parent, or educator, we have the tools and support you need to succeed. Don’t struggle with division any longer – let us help you master it!

Contact Information:

• Address: 123 Education Way, Learnville, CA 90210, United States
• WhatsApp: +1 555-555-1212
• Website: learns.edu.vn