Cost functions are fundamental to machine learning. This guide, presented by LEARNS.EDU.VN, provides a comprehensive understanding of what a cost function is, how it works, and why it is essential for training machine learning models. We’ll explore various cost functions, their applications, and how to choose the right one for your specific needs. Discover how cost functions optimize machine learning models, ensure accurate predictions, and enhance overall performance. Dive in to master this critical concept and elevate your expertise in model evaluation.
1. Understanding the Essence of Cost Functions in Machine Learning
The backbone of any machine learning model lies in its ability to learn from data and make accurate predictions. But how do we quantify “accuracy”? This is where the cost function steps in. Think of it as a judge, evaluating the model’s performance and providing a score that reflects how well it’s doing. The goal is to minimize this score, indicating that the model’s predictions are close to the actual values. A cost function, also known as a loss function, error function, or objective function, serves as a crucial element in the machine learning workflow, guiding the learning process and enabling models to improve their predictive capabilities, as discussed on LEARNS.EDU.VN. Key aspects include:
- Definition: A mathematical function that measures the discrepancy between predicted and actual values.
- Purpose: To quantify the error of a machine learning model.
- Role: Guiding the optimization process to find the best model parameters.
- Optimization: Aims to minimize (or maximize) the cost function to improve model performance.
- Examples: Mean Squared Error (MSE), Mean Absolute Error (MAE), Cross-Entropy.
1.1. The Core Objective: Minimizing Errors
The primary aim of a cost function is to provide a quantifiable measure of the error produced by a machine learning model. This measure is then used to refine the model’s parameters iteratively, enabling it to learn from data and enhance its predictive capabilities. By minimizing the cost function, we essentially guide the model to make more accurate predictions.
1.2. Types of Machine Learning Problems and Cost Functions
Cost functions vary based on the type of machine learning problem:
- Regression Problems: These problems involve predicting a continuous value, such as house prices or stock prices. Common cost functions include:
- Mean Squared Error (MSE): Calculates the average of the squares of the differences between predicted and actual values.
- Mean Absolute Error (MAE): Calculates the average of the absolute differences between predicted and actual values.
- Classification Problems: These problems involve categorizing data into predefined classes, such as identifying whether an email is spam or not. Common cost functions include:
- Cross-Entropy Loss: Measures the difference between the predicted probability distribution and the actual distribution.
- Hinge Loss: Used primarily in Support Vector Machines (SVMs) to maximize the margin between classes.
1.3. Understanding the Mathematical Foundation
To truly grasp the concept of cost functions, it’s essential to understand their mathematical underpinnings. A cost function is typically expressed as a mathematical equation that takes the model’s predictions and the actual values as inputs and outputs a single numerical value representing the error.
1.4. Visualizing Cost Functions
Visualizing cost functions can provide valuable insights into the optimization process. For example, consider a simple linear regression model with a single parameter, ‘w’. We can plot the cost function (e.g., MSE) as a function of ‘w’. The resulting graph will show a curve, and the goal is to find the value of ‘w’ that corresponds to the minimum point on this curve.
2. Diving Deep: Types of Cost Functions in Machine Learning
Different machine learning problems call for different cost functions. Let’s explore some of the most common types and their specific applications:
2.1. Regression Cost Functions
2.1.1. Mean Squared Error (MSE)
- Definition: The average of the squared differences between the predicted and actual values.
- Formula:
MSE = (1/n) * Σ(yᵢ – ŷᵢ)²
Where:- n is the number of data points.
- yᵢ is the actual value.
- ŷᵢ is the predicted value.
- Use Cases:
- Linear Regression
- Polynomial Regression
- Neural Networks for Regression
- Advantages:
- Differentiable, making it suitable for gradient-based optimization methods.
- Penalizes large errors more heavily, which can lead to better model performance in some cases.
- Disadvantages:
- Sensitive to outliers due to the squaring of errors.
- Can result in a model that is overly influenced by outliers.
2.1.2. Mean Absolute Error (MAE)
- Definition: The average of the absolute differences between the predicted and actual values.
- Formula:
MAE = (1/n) * Σ|yᵢ – ŷᵢ|
Where:- n is the number of data points.
- yᵢ is the actual value.
- ŷᵢ is the predicted value.
- Use Cases:
- Linear Regression
- Time Series Analysis
- Any regression problem where robustness to outliers is important.
- Advantages:
- Less sensitive to outliers compared to MSE.
- Provides a more robust measure of error when the data contains outliers.
- Disadvantages:
- Not differentiable at zero, which can cause issues with some optimization methods.
- Treats all errors equally, regardless of their magnitude.
2.1.3. Root Mean Squared Error (RMSE)
- Definition: The square root of the average of the squared differences between the predicted and actual values.
- Formula:
RMSE = √( (1/n) * Σ(yᵢ – ŷᵢ)² )
Where:- n is the number of data points.
- yᵢ is the actual value.
- ŷᵢ is the predicted value.
- Use Cases:
- Regression problems where the error needs to be in the same units as the target variable.
- Provides a more interpretable measure of error compared to MSE.
- Advantages:
- Differentiable, making it suitable for gradient-based optimization methods.
- Error is in the same units as the target variable, making it easier to interpret.
- Disadvantages:
- Sensitive to outliers due to the squaring of errors.
2.2. Classification Cost Functions
2.2.1. Binary Cross-Entropy Loss
- Definition: Measures the performance of a classification model where the output is a probability value between 0 and 1.
- Formula:
Binary Cross-Entropy = – (1/n) Σ[yᵢ log(ŷᵢ) + (1 – yᵢ) * log(1 – ŷᵢ)]
Where:- n is the number of data points.
- yᵢ is the actual value (0 or 1).
- ŷᵢ is the predicted probability.
- Use Cases:
- Binary Classification problems, such as spam detection or disease diagnosis.
- Advantages:
- Provides a good measure of the difference between predicted and actual probabilities.
- Differentiable, making it suitable for gradient-based optimization methods.
- Disadvantages:
- Can be sensitive to mislabeled data.
- Assumes that the predicted probabilities are well-calibrated.
2.2.2. Categorical Cross-Entropy Loss
- Definition: An extension of binary cross-entropy for multi-class classification problems.
- Formula:
Categorical Cross-Entropy = – (1/n) ΣΣ yᵢ,c log(ŷᵢ,c)
Where:- n is the number of data points.
- c is the number of classes.
- yᵢ,c is the actual value (0 or 1) for data point i and class c.
- ŷᵢ,c is the predicted probability for data point i and class c.
- Use Cases:
- Multi-class classification problems, such as image classification or text categorization.
- Advantages:
- Provides a good measure of the difference between predicted and actual probabilities for multiple classes.
- Differentiable, making it suitable for gradient-based optimization methods.
- Disadvantages:
- Can be sensitive to mislabeled data.
- Assumes that the predicted probabilities are well-calibrated.
2.2.3. Hinge Loss
- Definition: Used primarily in Support Vector Machines (SVMs) for binary classification problems.
- Formula:
Hinge Loss = (1/n) Σ max(0, 1 – yᵢ ŷᵢ)
Where:- n is the number of data points.
- yᵢ is the actual value (-1 or 1).
- ŷᵢ is the predicted value.
- Use Cases:
- Support Vector Machines (SVMs)
- Binary Classification problems where maximizing the margin between classes is important.
- Advantages:
- Maximizes the margin between classes, leading to better generalization performance.
- Robust to outliers.
- Disadvantages:
- Not differentiable, which can cause issues with some optimization methods.
- Can be sensitive to the choice of hyperparameters.
2.3. Other Cost Functions
2.3.1. Kullback-Leibler Divergence (KL Divergence)
- Definition: Measures how one probability distribution diverges from a second, expected probability distribution.
- Use Cases:
- Variational Autoencoders (VAEs)
- Generative models
- Advantages:
- Useful for measuring the similarity between probability distributions.
- Disadvantages:
- Not symmetric; KL(P||Q) is not necessarily equal to KL(Q||P).
2.3.2. Huber Loss
- Definition: A combination of MSE and MAE that is less sensitive to outliers than MSE.
- Use Cases:
- Regression problems where robustness to outliers is important.
- Advantages:
- Less sensitive to outliers compared to MSE.
- Differentiable, making it suitable for gradient-based optimization methods.
- Disadvantages:
- Requires tuning of the hyperparameter δ.
3. Optimizing Cost Functions: The Path to Model Perfection
Once we’ve defined our cost function, the next step is to minimize it. This is where optimization algorithms come into play. These algorithms iteratively adjust the model’s parameters to find the values that result in the lowest possible cost.
3.1. Gradient Descent: The Workhorse of Optimization
Gradient descent is one of the most widely used optimization algorithms in machine learning. It works by iteratively updating the model’s parameters in the direction of the negative gradient of the cost function. The gradient indicates the direction of the steepest increase in the cost function, so moving in the opposite direction will lead to a decrease in the cost.
3.2. Variants of Gradient Descent
- Batch Gradient Descent: Calculates the gradient using the entire training dataset in each iteration.
- Stochastic Gradient Descent (SGD): Calculates the gradient using a single randomly selected data point in each iteration.
- Mini-Batch Gradient Descent: Calculates the gradient using a small batch of randomly selected data points in each iteration.
3.3. Advanced Optimization Algorithms
- Adam (Adaptive Moment Estimation): Combines the advantages of AdaGrad and RMSProp, providing adaptive learning rates for each parameter.
- RMSProp (Root Mean Square Propagation): Adapts the learning rates based on the recent magnitudes of the gradients.
- AdaGrad (Adaptive Gradient Algorithm): Adapts the learning rates to parameters, performing larger updates for infrequent and smaller updates for frequent parameters.
4. How to Choose the Right Cost Function for Your Model
Selecting the appropriate cost function is crucial for achieving optimal model performance. The choice depends on various factors, including the type of machine learning problem, the characteristics of the data, and the desired properties of the model. Here’s a guide to help you make the right decision:
4.1. Consider the Type of Machine Learning Problem
- Regression: If you’re dealing with a regression problem, MSE, MAE, or RMSE are typically good choices.
- Classification: For classification problems, cross-entropy loss (binary or categorical) or hinge loss are commonly used.
4.2. Analyze the Data Characteristics
- Outliers: If your data contains outliers, MAE or Huber loss might be more robust than MSE.
- Data Distribution: If your data is highly skewed, consider using a cost function that is less sensitive to extreme values.
4.3. Think About the Desired Model Properties
- Interpretability: If you need a cost function that is easy to interpret, MAE might be a better choice than MSE.
- Sensitivity to Errors: If you want to penalize large errors more heavily, MSE might be a better choice than MAE.
4.4. Experiment and Iterate
- Try Different Cost Functions: Don’t be afraid to experiment with different cost functions and see which one works best for your specific problem.
- Monitor Performance: Keep a close eye on the model’s performance during training and validation to ensure that the chosen cost function is leading to the desired results.
5. Practical Examples: Cost Functions in Action
Let’s look at some practical examples of how cost functions are used in machine learning:
5.1. Linear Regression with MSE
In linear regression, the goal is to find the line that best fits the data. The MSE cost function measures the average squared difference between the predicted values (points on the line) and the actual values (data points). The optimization algorithm adjusts the slope and intercept of the line to minimize the MSE, resulting in the best-fit line.
5.2. Logistic Regression with Cross-Entropy Loss
In logistic regression, the goal is to predict the probability of a binary outcome (e.g., 0 or 1). The cross-entropy loss measures the difference between the predicted probabilities and the actual outcomes. The optimization algorithm adjusts the model’s parameters to minimize the cross-entropy loss, resulting in more accurate probability predictions.
5.3. Support Vector Machine with Hinge Loss
In Support Vector Machines (SVMs), the goal is to find the hyperplane that best separates the data into different classes. The hinge loss encourages the model to maximize the margin between the classes, leading to better generalization performance.
6. Advanced Topics: Beyond the Basics
Once you have a solid understanding of the basics of cost functions, you can delve into some more advanced topics:
6.1. Regularization
Regularization techniques, such as L1 and L2 regularization, can be added to the cost function to prevent overfitting. Overfitting occurs when the model learns the training data too well and performs poorly on new, unseen data. Regularization adds a penalty to the cost function based on the magnitude of the model’s parameters, encouraging the model to have smaller weights and be less complex.
6.2. Custom Cost Functions
In some cases, you may need to define your own custom cost function to address specific requirements of your problem. This allows you to tailor the cost function to your specific needs and potentially achieve better performance than using a standard cost function.
6.3. Cost Function Visualization
Visualizing the cost function during training can provide valuable insights into the optimization process. This can help you identify potential problems, such as oscillations or plateaus, and adjust the learning rate or other hyperparameters accordingly.
7. Common Mistakes to Avoid When Working with Cost Functions
Working with cost functions can be tricky, and it’s easy to make mistakes. Here are some common pitfalls to avoid:
7.1. Choosing the Wrong Cost Function
Selecting an inappropriate cost function can lead to suboptimal model performance. Make sure to carefully consider the type of machine learning problem, the characteristics of the data, and the desired properties of the model when choosing a cost function.
7.2. Ignoring Outliers
Outliers can have a significant impact on the cost function, especially when using MSE. Consider using a cost function that is more robust to outliers, such as MAE or Huber loss, or preprocess the data to remove or mitigate the effects of outliers.
7.3. Not Regularizing
Failing to regularize can lead to overfitting, especially when the model is complex or the training data is limited. Use regularization techniques, such as L1 or L2 regularization, to prevent overfitting and improve generalization performance.
7.4. Using a Fixed Learning Rate
Using a fixed learning rate can lead to slow convergence or oscillations during training. Consider using adaptive learning rate methods, such as Adam or RMSProp, to automatically adjust the learning rate during training.
7.5. Not Monitoring the Cost Function
Failing to monitor the cost function during training can make it difficult to identify potential problems and adjust the training process accordingly. Keep a close eye on the cost function and other metrics during training to ensure that the model is learning effectively.
8. Enhancing Learning with LEARNS.EDU.VN
At LEARNS.EDU.VN, we are committed to providing high-quality educational content that empowers you to excel in your learning journey. Whether you’re looking to acquire a new skill, deepen your understanding of a concept, or explore new areas of knowledge, we have something for you.
8.1. Comprehensive Guides
Our comprehensive guides cover a wide range of topics, from the fundamentals of machine learning to advanced techniques in data science. Each guide is carefully crafted to provide clear, concise, and actionable information that you can use to improve your skills and knowledge.
8.2. Expert Insights
Our team of experienced educators and industry experts share their insights and expertise to help you stay ahead of the curve. We provide real-world examples, case studies, and practical tips that you can use to apply what you’ve learned to your own projects and challenges.
8.3. Interactive Learning
We believe that learning should be interactive and engaging. That’s why we offer a variety of interactive learning tools, such as quizzes, exercises, and simulations, to help you reinforce your understanding and practice your skills.
8.4. Supportive Community
Join our supportive community of learners and connect with other like-minded individuals. Share your knowledge, ask questions, and get feedback from your peers and our team of experts.
9. Real-World Applications and Case Studies
To truly understand the importance of cost functions, let’s examine some real-world applications and case studies:
9.1. Predicting Housing Prices
In the real estate industry, predicting housing prices is a critical task. Machine learning models are used to analyze various factors, such as location, size, number of bedrooms, and amenities, to estimate the value of a property. Cost functions, such as MSE or RMSE, are used to train these models and ensure that they make accurate predictions.
9.2. Diagnosing Diseases
In the healthcare industry, machine learning models are used to diagnose diseases based on patient data, such as symptoms, medical history, and test results. Cost functions, such as cross-entropy loss, are used to train these models and ensure that they make accurate diagnoses.
9.3. Detecting Fraud
In the financial industry, machine learning models are used to detect fraudulent transactions. Cost functions, such as cross-entropy loss, are used to train these models and ensure that they accurately identify fraudulent activity.
9.4. Recommending Products
In the e-commerce industry, machine learning models are used to recommend products to customers based on their browsing history, purchase history, and other data. Cost functions, such as cross-entropy loss, are used to train these models and ensure that they make relevant and personalized recommendations.
10. The Future of Cost Functions in Machine Learning
As machine learning continues to evolve, so too will the role of cost functions. Here are some emerging trends and future directions in the field:
10.1. Development of New Cost Functions
Researchers are constantly developing new cost functions to address the limitations of existing ones and to tackle new challenges in machine learning. These new cost functions may be more robust to outliers, more efficient to optimize, or better suited to specific types of machine learning problems.
10.2. Adaptive Cost Functions
Adaptive cost functions are designed to automatically adjust their behavior based on the characteristics of the data or the performance of the model. This can lead to more efficient training and better generalization performance.
10.3. Cost Function Learning
Cost function learning involves using machine learning to learn the optimal cost function for a given problem. This can be particularly useful when it is difficult to define a cost function manually.
10.4. Integration with Deep Learning
Cost functions are an integral part of deep learning, and researchers are exploring new ways to integrate cost functions with deep learning architectures. This includes developing new cost functions that are specifically designed for deep learning models and exploring new ways to optimize cost functions in deep learning.
11. Numerical Analysis of Cost Functions
Cost functions are evaluated numerically to gauge the performance of machine learning models. Key metrics include error rates, computational efficiency, and stability under varying datasets. Analyzing these functions involves employing statistical methods to assess their sensitivity to outliers, bias, and variance. Numerical simulations and visualizations provide critical insights into the cost function’s behavior, aiding in the selection of appropriate optimization algorithms and fine-tuning of model parameters. These analyses ensure robust and reliable model performance across diverse applications.
12. Cost Functions and Ethical Considerations
The design and application of cost functions in machine learning carry significant ethical implications. It’s crucial to ensure that these functions do not inadvertently perpetuate or amplify biases present in the training data, leading to unfair or discriminatory outcomes. Careful attention must be paid to the selection and potential impact of cost functions, striving for equitable and transparent model performance. This involves regularly auditing models for bias and making adjustments to promote fairness and inclusivity. Ethical considerations are not just about technical correctness but also about the broader societal impact of machine learning systems.
13. Cost Functions for Reinforcement Learning
In reinforcement learning, cost functions, often termed reward functions, guide agents in learning optimal behaviors by quantifying the desirability of different actions and states. These functions define the goals of the agent, incentivizing actions that lead to higher rewards and penalizing those that result in lower rewards or undesirable states. Designing effective reward functions is crucial for successful reinforcement learning, as they directly influence the agent’s learning trajectory and the quality of the learned policy. Careful crafting ensures alignment with desired outcomes, avoids unintended behaviors, and promotes efficient learning.
14. Cost Functions in Unsupervised Learning
In unsupervised learning, cost functions are used to measure the quality of the learned representations or structures within the data. Unlike supervised learning, there are no explicit target values to compare against. Instead, cost functions in unsupervised learning focus on properties such as data reconstruction accuracy (as in autoencoders), cluster cohesion and separation (as in clustering algorithms), or density estimation (as in generative models). These functions guide the learning process by quantifying how well the model captures the underlying patterns and relationships in the data, enabling the discovery of meaningful insights without labeled supervision.
15. FAQ Section: Your Burning Questions Answered
Here are some frequently asked questions about cost functions in machine learning:
Q1: What is a cost function in machine learning?
A cost function is a mathematical function that measures the discrepancy between the predicted and actual values in a machine learning model. It quantifies the error of the model and guides the optimization process to find the best model parameters.
Q2: Why are cost functions important?
Cost functions are essential because they provide a way to evaluate the performance of a machine learning model and guide the optimization process. By minimizing the cost function, we can improve the model’s accuracy and predictive capabilities.
Q3: What are some common types of cost functions?
Some common types of cost functions include Mean Squared Error (MSE), Mean Absolute Error (MAE), Cross-Entropy Loss, and Hinge Loss.
Q4: How do I choose the right cost function for my model?
The choice of cost function depends on various factors, including the type of machine learning problem, the characteristics of the data, and the desired properties of the model.
Q5: What is gradient descent?
Gradient descent is an optimization algorithm used to minimize the cost function by iteratively updating the model’s parameters in the direction of the negative gradient of the cost function.
Q6: What is regularization?
Regularization is a technique used to prevent overfitting by adding a penalty to the cost function based on the magnitude of the model’s parameters.
Q7: Can I define my own custom cost function?
Yes, in some cases, you may need to define your own custom cost function to address specific requirements of your problem.
Q8: What are some common mistakes to avoid when working with cost functions?
Some common mistakes include choosing the wrong cost function, ignoring outliers, not regularizing, using a fixed learning rate, and not monitoring the cost function.
Q9: How are cost functions used in deep learning?
Cost functions are an integral part of deep learning and are used to train deep neural networks. Researchers are exploring new ways to integrate cost functions with deep learning architectures to improve performance and efficiency.
Q10: Where can I learn more about cost functions?
You can learn more about cost functions at LEARNS.EDU.VN, where we provide comprehensive guides, expert insights, and interactive learning tools to help you master machine learning.
16. Conclusion: Mastering Cost Functions for Machine Learning Success
Cost functions are the unsung heroes of machine learning. They provide the crucial feedback loop that allows models to learn from data and make accurate predictions. By understanding the different types of cost functions, how they work, and how to choose the right one for your specific needs, you can unlock the full potential of machine learning and achieve remarkable results. Embrace the power of cost functions and embark on a journey of continuous learning and improvement with LEARNS.EDU.VN. Remember, the path to model perfection starts with a well-defined cost function. For additional resources or questions, feel free to reach out: Address: 123 Education Way, Learnville, CA 90210, United States. Whatsapp: +1 555-555-1212. Website: LEARNS.EDU.VN.
By focusing on minimizing cost functions, machine learning models can provide valuable insights and make accurate predictions across a wide range of applications.
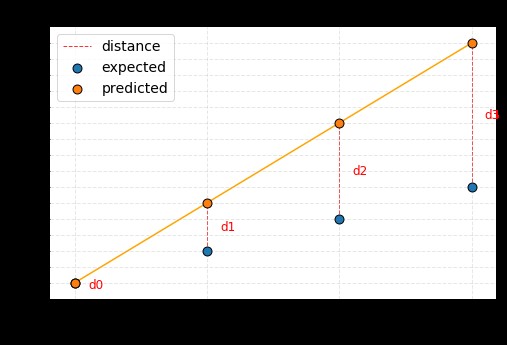Cost function optimization
17. Call to Action
Ready to take your machine learning skills to the next level? Visit LEARNS.EDU.VN today to discover a wealth of resources, including comprehensive guides, expert insights, and interactive learning tools. Whether you’re a beginner or an experienced practitioner, we have something to help you achieve your goals. Don’t miss out on the opportunity to unlock your full potential and become a master of machine learning. Join the learns.edu.vn community today and start your journey to success!
