The Pythagorean Theorem, a cornerstone of geometry, is typically introduced in middle school, around 7th or 8th grade. This article on LEARNS.EDU.VN delves into when and how this crucial concept is taught, exploring its applications and relevance across various educational levels and real-world scenarios. Grasping this theorem unlocks numerous problem-solving skills and provides a foundation for advanced mathematical studies, fostering analytical thinking and practical application in fields ranging from architecture to navigation.
1. What is the Pythagorean Theorem and Why is it Important?
The Pythagorean Theorem is a fundamental principle in geometry that describes the relationship between the sides of a right triangle. Specifically, it states that the sum of the squares of the two shorter sides (legs or cathetus) of a right triangle is equal to the square of the longest side (hypotenuse). This relationship is expressed by the equation a² + b² = c², where ‘a’ and ‘b’ are the lengths of the legs, and ‘c’ is the length of the hypotenuse.
1.1 Understanding the Basics of the Pythagorean Theorem
To fully understand the Pythagorean Theorem, it’s essential to define each component clearly:
- Right Triangle: A triangle with one angle measuring exactly 90 degrees.
- Legs (Cathetus): The two sides that form the right angle.
- Hypotenuse: The side opposite the right angle, which is also the longest side of the triangle.
The theorem provides a method to calculate the length of one side of a right triangle if the lengths of the other two sides are known. For example, if a = 3 and b = 4, then c² = 3² + 4² = 9 + 16 = 25, and c = √25 = 5.
1.2 Historical Significance of the Pythagorean Theorem
The Pythagorean Theorem is named after the ancient Greek mathematician Pythagoras, although evidence suggests that the concept was known in other cultures long before Pythagoras. Babylonian mathematicians, for instance, had knowledge of Pythagorean triples (sets of three positive integers that satisfy the theorem) as early as 1800 BC. Pythagoras and his followers are credited with providing the first known proof of the theorem, which has since become a cornerstone of mathematical education.
1.3 Real-World Applications of the Pythagorean Theorem
The Pythagorean Theorem is not just a theoretical concept; it has numerous practical applications in various fields:
- Construction: Builders use the theorem to ensure that buildings are square and corners are right angles.
- Navigation: Navigators use it to calculate distances and plan routes.
- Engineering: Engineers apply it to design structures and solve problems related to force and motion.
- Architecture: Architects use it to design buildings and calculate dimensions.
- Surveying: Surveyors use it to measure land and create accurate maps.
For example, a construction worker might use the Pythagorean Theorem to ensure that the walls of a room are perfectly vertical and that the corners are square. By measuring the lengths of the walls and the diagonal distance across the room, they can verify that the room is rectangular and that the angles are 90 degrees.
1.4 Foundational Importance in Mathematics
The Pythagorean Theorem serves as a foundational concept for more advanced topics in mathematics. It is used in:
- Trigonometry: The theorem is essential for understanding trigonometric functions and relationships.
- Calculus: It is used in various calculus concepts, such as finding distances and rates of change.
- Analytic Geometry: It is used to define distances and relationships in coordinate systems.
Because of its widespread applications and its role in laying the groundwork for advanced mathematical studies, the Pythagorean Theorem is a critical concept for students to master.
2. What Grade Level is the Pythagorean Theorem Typically Taught?
The Pythagorean Theorem is typically introduced in middle school, specifically around the 7th or 8th grade. This placement allows students to have the necessary background in basic geometry and algebra to understand and apply the theorem effectively. The timing can vary slightly depending on the school district and the curriculum.
2.1 Curriculum Standards and the Pythagorean Theorem
Most state and national curriculum standards, including the Common Core State Standards in the United States, include the Pythagorean Theorem as a key topic in the middle school math curriculum. These standards ensure that students are introduced to the theorem and its applications at an appropriate stage in their mathematical development.
2.2 Prerequisites for Learning the Pythagorean Theorem
Before students can successfully learn and apply the Pythagorean Theorem, they typically need to have a solid understanding of several prerequisite concepts, including:
- Basic Geometry: Familiarity with shapes, angles, and the properties of triangles.
- Algebra: Knowledge of variables, equations, and basic algebraic operations, such as solving for an unknown.
- Squares and Square Roots: Understanding how to calculate the square of a number and find the square root of a number.
These prerequisites ensure that students can manipulate the equation a² + b² = c² and solve for unknown side lengths effectively.
2.3 How the Pythagorean Theorem Fits into the Math Curriculum
The Pythagorean Theorem is often taught as part of a broader unit on geometry and measurement. It typically follows the introduction of basic geometric concepts and leads into more advanced topics, such as trigonometry. The theorem provides a practical application of algebraic principles and helps students see the connection between algebra and geometry.
For example, after learning about triangles and angles, students might be introduced to the Pythagorean Theorem to solve problems involving right triangles. This knowledge then leads to the study of trigonometric ratios, such as sine, cosine, and tangent, which are based on the relationships between the sides of right triangles.
2.4 Adjustments for Different Learning Levels
Teachers often adjust their approach to teaching the Pythagorean Theorem based on the learning levels of their students. For students who are struggling, teachers may provide additional support and practice with the prerequisite concepts. For advanced students, teachers may introduce more challenging problems and applications of the theorem.
- For struggling students: Focus on concrete examples and hands-on activities to illustrate the theorem.
- For advanced students: Explore more complex problems and applications, such as finding the distance between two points in a coordinate plane.
By tailoring their instruction to meet the needs of all learners, teachers can ensure that all students have the opportunity to master the Pythagorean Theorem.
3. Step-by-Step Guide to Learning the Pythagorean Theorem
Learning the Pythagorean Theorem involves understanding the underlying concepts and applying them to solve problems. Here’s a step-by-step guide to help students master this important mathematical principle:
3.1 Step 1: Understand the Concept of a Right Triangle
The first step in learning the Pythagorean Theorem is to understand the concept of a right triangle. Students should be able to identify the right angle, the legs, and the hypotenuse.
- Identify the Right Angle: Look for the angle that measures 90 degrees, often marked with a small square.
- Identify the Legs: These are the two sides that form the right angle.
- Identify the Hypotenuse: This is the side opposite the right angle, which is also the longest side of the triangle.
Once students can confidently identify these components, they are ready to move on to the next step.
3.2 Step 2: Learn the Formula a² + b² = c²
The next step is to learn the formula a² + b² = c², which represents the relationship between the sides of a right triangle. Students should understand that ‘a’ and ‘b’ represent the lengths of the legs, and ‘c’ represents the length of the hypotenuse.
- Understand the Variables: Make sure students know what each variable represents in the formula.
- Practice with Simple Numbers: Start with simple numbers to illustrate the formula. For example, if a = 3 and b = 4, then c² = 3² + 4² = 9 + 16 = 25, and c = √25 = 5.
- Use Visual Aids: Use diagrams and visual aids to help students see the relationship between the sides of the triangle and the formula.
3.3 Step 3: Practice Solving for the Hypotenuse
The most common type of problem involving the Pythagorean Theorem is solving for the hypotenuse. Given the lengths of the two legs, students must use the formula to find the length of the hypotenuse.
- Example Problem: A right triangle has legs of length 6 and 8. Find the length of the hypotenuse.
- Solution:
- a = 6, b = 8
- c² = a² + b²
- c² = 6² + 8²
- c² = 36 + 64
- c² = 100
- c = √100
- c = 10
3.4 Step 4: Practice Solving for a Leg
Another type of problem involves solving for one of the legs, given the lengths of the hypotenuse and the other leg.
- Example Problem: A right triangle has a hypotenuse of length 13 and one leg of length 5. Find the length of the other leg.
- Solution:
- c = 13, a = 5
- a² + b² = c²
- 5² + b² = 13²
- 25 + b² = 169
- b² = 169 – 25
- b² = 144
- b = √144
- b = 12
3.5 Step 5: Apply the Theorem to Real-World Problems
The final step is to apply the Pythagorean Theorem to real-world problems. This helps students see the practical applications of the theorem and reinforces their understanding of the concepts.
- Example Problem: A ladder is leaning against a wall. The ladder is 10 feet long, and the base of the ladder is 6 feet from the wall. How high up the wall does the ladder reach?
- Solution:
- c = 10, a = 6
- a² + b² = c²
- 6² + b² = 10²
- 36 + b² = 100
- b² = 100 – 36
- b² = 64
- b = √64
- b = 8
Therefore, the ladder reaches 8 feet up the wall.
3.6 Tips for Mastering the Pythagorean Theorem
To help students master the Pythagorean Theorem, here are some additional tips:
- Practice Regularly: The more students practice, the better they will become at applying the theorem.
- Use Visual Aids: Diagrams and visual aids can help students see the relationship between the sides of the triangle and the formula.
- Work Through Examples: Work through plenty of examples to reinforce the concepts and build confidence.
- Seek Help When Needed: Don’t be afraid to ask for help from a teacher, tutor, or classmate if you are struggling with the material.
- Apply to Real-World Situations: Look for opportunities to apply the theorem to real-world situations to see its practical applications.
4. Common Challenges Students Face with the Pythagorean Theorem
While the Pythagorean Theorem is a fundamental concept, many students encounter challenges when learning and applying it. Understanding these common pitfalls can help educators and students address them effectively.
4.1 Difficulty Identifying the Hypotenuse
One of the most common challenges is identifying the hypotenuse of a right triangle. Students may confuse the hypotenuse with one of the legs, leading to incorrect calculations.
- Why it happens: The hypotenuse is always the longest side and is opposite the right angle. Students may not fully grasp this relationship.
- How to address it: Provide plenty of practice identifying the hypotenuse in different orientations of right triangles. Use visual aids and diagrams to reinforce the concept.
4.2 Confusion with the Formula
Another challenge is confusion with the formula a² + b² = c². Students may mix up the variables or forget to square the numbers before adding them.
- Why it happens: The formula involves multiple steps, and students may not fully understand the order of operations.
- How to address it: Break down the formula into smaller steps and provide plenty of practice with each step. Use mnemonic devices or visual aids to help students remember the formula.
4.3 Algebraic Errors
Solving for an unknown side length involves algebraic manipulation, which can be challenging for some students. Errors in algebra can lead to incorrect answers.
- Why it happens: Students may struggle with basic algebraic operations, such as solving for an unknown variable or simplifying expressions.
- How to address it: Review basic algebra skills and provide additional support for students who are struggling. Break down the algebraic steps into smaller, more manageable tasks.
4.4 Application to Real-World Problems
Applying the Pythagorean Theorem to real-world problems can be difficult for students who struggle to translate word problems into mathematical equations.
- Why it happens: Students may have difficulty identifying the relevant information in a word problem and translating it into a mathematical equation.
- How to address it: Provide plenty of practice with real-world problems and help students break down the problems into smaller steps. Encourage students to draw diagrams and label the sides of the triangle to help them visualize the problem.
4.5 Forgetting the Square Root
After finding c², students must take the square root to find the length of the hypotenuse. Forgetting this final step is a common error.
- Why it happens: Students may focus on the initial steps of the problem and forget to complete the final step.
- How to address it: Emphasize the importance of taking the square root and provide plenty of practice with this step. Encourage students to double-check their work to ensure that they have completed all the necessary steps.
4.6 Misunderstanding Pythagorean Triples
Pythagorean triples are sets of three positive integers that satisfy the Pythagorean Theorem (e.g., 3, 4, 5). Students may try to apply these triples to non-right triangles or misuse them.
- Why it happens: Students may not fully understand the conditions under which Pythagorean triples can be used.
- How to address it: Clearly explain the concept of Pythagorean triples and provide examples of how they can be used. Emphasize that these triples only apply to right triangles.
5. Tips and Tricks for Teaching the Pythagorean Theorem Effectively
Teaching the Pythagorean Theorem effectively requires a combination of clear explanations, engaging activities, and targeted support. Here are some tips and tricks to help educators teach this important concept:
5.1 Use Visual Aids and Manipulatives
Visual aids and manipulatives can help students understand the Pythagorean Theorem more concretely.
- Diagrams: Use diagrams to illustrate the relationship between the sides of a right triangle and the formula a² + b² = c².
- Manipulatives: Use manipulatives, such as square tiles or blocks, to demonstrate that the sum of the squares of the legs is equal to the square of the hypotenuse.
- Interactive Whiteboard: Use an interactive whiteboard to draw right triangles and label the sides. You can also use it to solve problems and show the steps involved.
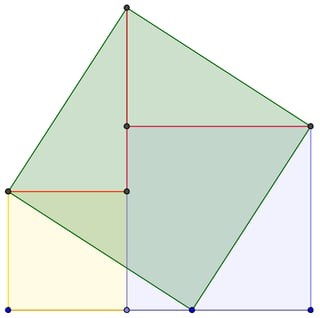Pythagorean Theorem Visual
5.2 Relate to Real-World Examples
Connecting the Pythagorean Theorem to real-world examples can help students see the practical applications of the concept.
- Construction: Discuss how builders use the theorem to ensure that buildings are square and corners are right angles.
- Navigation: Explain how navigators use it to calculate distances and plan routes.
- Sports: Discuss how athletes use it to calculate distances and angles in sports such as baseball or soccer.
5.3 Break Down the Formula into Smaller Steps
The formula a² + b² = c² can be intimidating for some students. Breaking it down into smaller steps can make it more manageable.
- Explain Each Variable: Make sure students understand what each variable represents in the formula.
- Practice with Simple Numbers: Start with simple numbers to illustrate the formula.
- Use Visual Aids: Use diagrams and visual aids to help students see the relationship between the sides of the triangle and the formula.
5.4 Provide Plenty of Practice
Practice is essential for mastering the Pythagorean Theorem. Provide plenty of opportunities for students to practice solving problems.
- Worksheets: Use worksheets with a variety of problems to provide practice.
- Online Resources: Use online resources, such as interactive websites or videos, to provide additional practice.
- Group Activities: Use group activities to provide opportunities for students to work together and learn from each other.
5.5 Use Technology
Technology can be a valuable tool for teaching the Pythagorean Theorem.
- Interactive Websites: Use interactive websites to provide virtual manipulatives and simulations.
- Videos: Use videos to explain the concept and provide examples of how to solve problems.
- Apps: Use apps to provide practice and assessment.
5.6 Address Common Misconceptions
Address common misconceptions about the Pythagorean Theorem to prevent students from making errors.
- Identifying the Hypotenuse: Emphasize that the hypotenuse is always the longest side and is opposite the right angle.
- Using the Formula: Make sure students understand the formula a² + b² = c² and how to use it correctly.
- Applying to Real-World Problems: Provide plenty of practice with real-world problems and help students break down the problems into smaller steps.
5.7 Differentiate Instruction
Differentiate instruction to meet the needs of all learners.
- For struggling students: Provide additional support and practice with the prerequisite concepts.
- For advanced students: Introduce more challenging problems and applications of the theorem.
- Use a variety of instructional strategies: Use a variety of instructional strategies, such as visual aids, manipulatives, and technology, to engage all learners.
By following these tips and tricks, educators can teach the Pythagorean Theorem effectively and help students master this important mathematical concept.
6. Advanced Applications of the Pythagorean Theorem
Beyond the basic calculations involving right triangles, the Pythagorean Theorem has numerous advanced applications in various fields. Exploring these applications can provide a deeper understanding of the theorem’s significance.
6.1 Distance Formula
The distance formula, used to calculate the distance between two points in a coordinate plane, is derived directly from the Pythagorean Theorem. Given two points (x₁, y₁) and (x₂, y₂), the distance d between them is:
d = √((x₂ – x₁)² + (y₂ – y₁)²).
This formula is based on the Pythagorean Theorem, where the distance between the points is the hypotenuse of a right triangle, and the differences in the x and y coordinates are the legs.
6.2 Trigonometry
The Pythagorean Theorem is foundational to trigonometry, which studies the relationships between the angles and sides of triangles. Trigonometric functions, such as sine, cosine, and tangent, are defined based on the ratios of the sides of a right triangle.
- Sine (sin): The ratio of the length of the opposite side to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the adjacent side to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the opposite side to the length of the adjacent side.
These functions are used in various applications, such as navigation, surveying, and engineering.
6.3 3D Geometry
The Pythagorean Theorem can be extended to three-dimensional space to calculate distances and solve problems involving three-dimensional objects. For example, the distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) in 3D space is:
d = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²)
This formula is an extension of the Pythagorean Theorem, where the distance is the hypotenuse of a right triangle in three dimensions.
6.4 Physics
In physics, the Pythagorean Theorem is used in various contexts, such as calculating the magnitude of vectors, analyzing forces, and solving problems involving motion.
- Vectors: The magnitude of a vector with components x and y is √(x² + y²).
- Forces: The resultant force of two perpendicular forces is √(F₁² + F₂²).
- Motion: The displacement of an object moving in two dimensions can be calculated using the Pythagorean Theorem.
6.5 Computer Graphics
The Pythagorean Theorem is used in computer graphics to calculate distances, determine the positions of objects, and create realistic images.
- Distance Calculations: Used to calculate the distance between objects in a 3D scene.
- Object Placement: Used to position objects correctly in a 3D scene.
- Rendering: Used to calculate lighting and shading effects.
6.6 Navigation and Surveying
In navigation and surveying, the Pythagorean Theorem is used to calculate distances, determine positions, and create accurate maps.
- Distance Calculations: Used to calculate the distance between two points on the Earth’s surface.
- Positioning: Used in GPS systems to determine the location of a device.
- Mapping: Used to create accurate maps of land and sea.
6.7 Engineering and Architecture
Engineers and architects use the Pythagorean Theorem to design structures, calculate dimensions, and ensure stability.
- Structural Design: Used to calculate the lengths of structural components and ensure that buildings are stable.
- Dimension Calculations: Used to calculate the dimensions of rooms, buildings, and other structures.
- Stability Analysis: Used to analyze the stability of structures and ensure that they can withstand various loads.
7. How to Practice the Pythagorean Theorem with Fun Activities
Learning the Pythagorean Theorem doesn’t have to be dry and boring. There are many fun and engaging activities that can help students practice and master this important concept.
7.1 Pythagorean Theorem Scavenger Hunt
Create a scavenger hunt where students must use the Pythagorean Theorem to find hidden clues.
- How it works: Hide clues around the classroom or school, and provide students with problems that require them to use the Pythagorean Theorem to find the location of the next clue.
- Benefits: This activity gets students moving and engaged while practicing the Pythagorean Theorem.
7.2 Building a Pythagorean Theorem Model
Have students build a model that demonstrates the Pythagorean Theorem.
- How it works: Provide students with materials such as cardboard, construction paper, and scissors, and have them build a model that shows that the sum of the squares of the legs is equal to the square of the hypotenuse.
- Benefits: This activity helps students visualize the theorem and understand its underlying principles.
7.3 Pythagorean Theorem Bingo
Create bingo cards with problems that require students to use the Pythagorean Theorem.
- How it works: Call out problems and have students solve them. If the answer is on their bingo card, they can mark it off. The first student to get bingo wins.
- Benefits: This activity is a fun and engaging way to practice the Pythagorean Theorem.
7.4 Real-World Problem Solving Challenge
Challenge students to solve real-world problems using the Pythagorean Theorem.
- How it works: Provide students with scenarios such as calculating the height of a tree or the distance across a lake, and have them use the Pythagorean Theorem to solve the problem.
- Benefits: This activity helps students see the practical applications of the theorem and reinforces their understanding of the concepts.
7.5 Pythagorean Theorem Art Project
Have students create an art project that incorporates the Pythagorean Theorem.
- How it works: Provide students with materials such as graph paper, rulers, and colored pencils, and have them create a design that uses right triangles and the Pythagorean Theorem.
- Benefits: This activity combines math and art, making learning more engaging and creative.
7.6 Online Pythagorean Theorem Games
There are many online games and interactive activities that can help students practice the Pythagorean Theorem.
- How it works: Find online games or activities that provide practice with solving problems involving the Pythagorean Theorem.
- Benefits: These games can be a fun and engaging way to practice the theorem and reinforce understanding.
By incorporating these fun activities into your teaching, you can help students master the Pythagorean Theorem while keeping them engaged and motivated.
8. Resources for Further Learning and Practice
To further enhance understanding and proficiency in the Pythagorean Theorem, numerous resources are available for both students and educators. These resources offer additional explanations, practice problems, and real-world applications.
8.1 Online Educational Platforms
Several online educational platforms offer comprehensive lessons and practice exercises on the Pythagorean Theorem.
- Khan Academy: Provides free video tutorials and practice exercises covering the Pythagorean Theorem and related concepts.
- IXL: Offers interactive practice exercises with immediate feedback and progress tracking.
- mathantics.com: Features clear and concise video lessons that explain the Pythagorean Theorem in an easy-to-understand manner.
8.2 Textbooks and Workbooks
Traditional textbooks and workbooks remain valuable resources for learning and practicing the Pythagorean Theorem.
- Geometry Textbooks: Most geometry textbooks include a chapter dedicated to the Pythagorean Theorem, with detailed explanations and practice problems.
- Practice Workbooks: Workbooks offer a wide variety of practice problems, ranging from basic to advanced, to help students master the theorem.
8.3 Online Calculators and Tools
Online calculators and tools can assist with solving problems and checking answers.
- Pythagorean Theorem Calculator: Online calculators that allow students to input the lengths of two sides of a right triangle and calculate the length of the third side.
- Graphing Calculators: Calculators with graphing capabilities can be used to visualize right triangles and explore the relationships between their sides.
8.4 Educational Websites and Blogs
Educational websites and blogs often feature articles, tutorials, and tips for learning and teaching the Pythagorean Theorem.
- LEARNS.EDU.VN: Offers articles and resources on various mathematical topics, including the Pythagorean Theorem, providing detailed explanations and practical examples.
- Math is Fun: Features clear explanations and interactive activities for learning the Pythagorean Theorem.
- Purplemath: Provides detailed lessons and examples on the Pythagorean Theorem and related concepts.
8.5 Videos and Tutorials
Videos and tutorials can provide visual explanations and step-by-step guidance on solving problems involving the Pythagorean Theorem.
- YouTube: Numerous channels offer video tutorials on the Pythagorean Theorem, ranging from basic introductions to advanced applications.
- TeacherTube: Features videos created by teachers and educators, providing instructional content on the Pythagorean Theorem.
8.6 Apps and Mobile Resources
Mobile apps can provide convenient access to lessons, practice exercises, and calculators for learning the Pythagorean Theorem on the go.
- Pythagorean Theorem Apps: Apps available for iOS and Android devices that offer practice problems, calculators, and interactive lessons.
- Geometry Apps: Apps that cover various geometry topics, including the Pythagorean Theorem, with interactive features and visual aids.
By utilizing these resources, students and educators can enhance their understanding of the Pythagorean Theorem and develop the skills necessary to apply it effectively in various contexts.
9. Why LEARNS.EDU.VN is Your Best Resource for Math Education
When it comes to mastering mathematical concepts like the Pythagorean Theorem, having access to reliable and comprehensive resources is crucial. LEARNS.EDU.VN stands out as an exceptional platform for math education, offering a wide range of tools and materials designed to cater to learners of all levels.
9.1 Comprehensive and Detailed Explanations
LEARNS.EDU.VN provides in-depth explanations of mathematical concepts, ensuring that students grasp the underlying principles before moving on to more complex applications. The Pythagorean Theorem is explained with clear and concise language, supported by visual aids and examples that make it easier to understand.
9.2 Wide Range of Practice Problems
Practice is essential for mastering any mathematical concept, and LEARNS.EDU.VN offers a vast collection of practice problems to help students hone their skills. These problems range from basic to advanced, allowing students to gradually build their confidence and proficiency.
9.3 Real-World Applications
LEARNS.EDU.VN emphasizes the practical applications of mathematical concepts, demonstrating how they are used in various fields and industries. This helps students see the relevance of what they are learning and motivates them to engage more deeply with the material.
9.4 Interactive Learning Tools
The platform offers a variety of interactive learning tools, such as calculators, graphing utilities, and simulations, to enhance the learning experience. These tools allow students to explore mathematical concepts in a hands-on and engaging way.
9.5 Expert-Created Content
The content on LEARNS.EDU.VN is created by experienced educators and mathematicians who are passionate about making math accessible to all learners. This ensures that the material is accurate, up-to-date, and aligned with curriculum standards.
9.6 Personalized Learning Experience
LEARNS.EDU.VN offers a personalized learning experience, allowing students to track their progress, identify areas where they need improvement, and receive targeted support. This helps students stay motivated and focused on their learning goals.
9.7 Accessible Anytime, Anywhere
The platform is accessible anytime, anywhere, making it easy for students to learn at their own pace and on their own schedule. Whether you are studying at home, in the library, or on the go, LEARNS.EDU.VN is always available to support your learning journey.
9.8 Support from Expert Educators
At LEARNS.EDU.VN, we understand that learning math can sometimes be challenging. That’s why we offer expert educators to guide you through your learning journey. Our team of experienced math teachers and tutors is dedicated to providing personalized support and answering any questions you may have.
Whether you’re struggling with a specific concept or need help with problem-solving, our experts are here to help. They can provide one-on-one tutoring, answer questions via email or chat, and offer feedback on your work. With LEARNS.EDU.VN, you’re never alone in your quest to master math.
With its comprehensive resources, expert-created content, and personalized learning experience, LEARNS.EDU.VN is the ideal platform for mastering the Pythagorean Theorem and other mathematical concepts. Whether you are a student, educator, or lifelong learner, LEARNS.EDU.VN can help you achieve your math goals.
Ready to explore the world of mathematics with confidence? Visit LEARNS.EDU.VN today and unlock your full potential.
10. Frequently Asked Questions (FAQs) About When You Learn the Pythagorean Theorem
To address common queries and misconceptions about the Pythagorean Theorem, here are some frequently asked questions:
10.1 What is the Pythagorean Theorem?
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This is expressed as a² + b² = c², where ‘a’ and ‘b’ are the lengths of the legs, and ‘c’ is the length of the hypotenuse.
10.2 When is the Pythagorean Theorem Typically Taught?
The Pythagorean Theorem is typically introduced in middle school, around the 7th or 8th grade. This timing allows students to have the necessary background in basic geometry and algebra to understand and apply the theorem effectively.
10.3 What are the Prerequisites for Learning the Pythagorean Theorem?
Before learning the Pythagorean Theorem, students should have a solid understanding of basic geometry, algebra, squares, and square roots.
10.4 Why is the Pythagorean Theorem Important?
The Pythagorean Theorem is important because it is a fundamental concept in geometry with numerous practical applications in fields such as construction, navigation, engineering, and architecture. It also serves as a foundation for more advanced topics in mathematics, such as trigonometry and calculus.
10.5 How is the Pythagorean Theorem Used in Real Life?
The Pythagorean Theorem is used in various real-life situations, such as calculating distances, designing structures, and navigating routes. For example, construction workers use it to ensure that buildings are square and corners are right angles, while navigators use it to calculate distances and plan routes.
10.6 What are Some Common Challenges Students Face When Learning the Pythagorean Theorem?
Some common challenges students face when learning the Pythagorean Theorem include difficulty identifying the hypotenuse, confusion with the formula, algebraic errors, and application to real-world problems.
10.7 How Can Teachers Help Students Overcome These Challenges?
Teachers can help students overcome these challenges by using visual aids, breaking down the formula into smaller steps, providing plenty of practice, and relating the theorem to real-world examples.
10.8 Are There Any Fun Activities to Practice the Pythagorean Theorem?
Yes, there are many fun activities to practice the Pythagorean Theorem, such as scavenger hunts, building models, bingo games, and art projects.
10.9 What Resources are Available for Further Learning and Practice?
Numerous resources are available for further learning and practice, including online educational platforms, textbooks, workbooks, online calculators, educational websites, videos, and mobile apps.
10.10 Where Can I Find More Information and Support for Learning the Pythagorean Theorem?
You can find more information and support for learning the Pythagorean Theorem at LEARNS.EDU.VN, which offers comprehensive explanations, practice problems, interactive tools, and expert-created content.
By addressing these frequently asked questions, students and educators can gain a better understanding of the Pythagorean Theorem and its applications.
Unlock a world of mathematical knowledge and skills with LEARNS.EDU.VN. Visit our website today at learns.edu.vn or contact us at 123 Education Way, Learnville, CA 90210, United States, or Whatsapp: +1 555-555-1212. Start your journey to math excellence now!
