Machine Learning Support Vector Machines: A Comprehensive Guide

Machine Learning Support Vector Machines (SVMs) are powerful supervised learning models utilized for classification, regression, and outlier detection. This comprehensive guide, brought to you by LEARNS.EDU.VN, delves into the fundamentals of SVMs, exploring their working principles, diverse types, and real-world applications. Discover how SVMs can transform data to identify optimal boundaries, empowering you with the knowledge to tackle complex analytical challenges. Explore advanced techniques and gain practical insights into applying SVMs in various domains, unlocking their potential for enhanced decision-making and innovation.

1. Understanding Support Vector Machines

A Support Vector Machine (SVM) is a versatile machine learning algorithm that employs supervised learning techniques. SVMs excel at solving complex classification, regression, and outlier detection problems. They achieve this by performing optimal data transformations to determine boundaries between data points based on predefined classes, labels, or outputs. SVMs are invaluable tools across various disciplines, including healthcare, natural language processing, signal processing, and image and speech recognition.

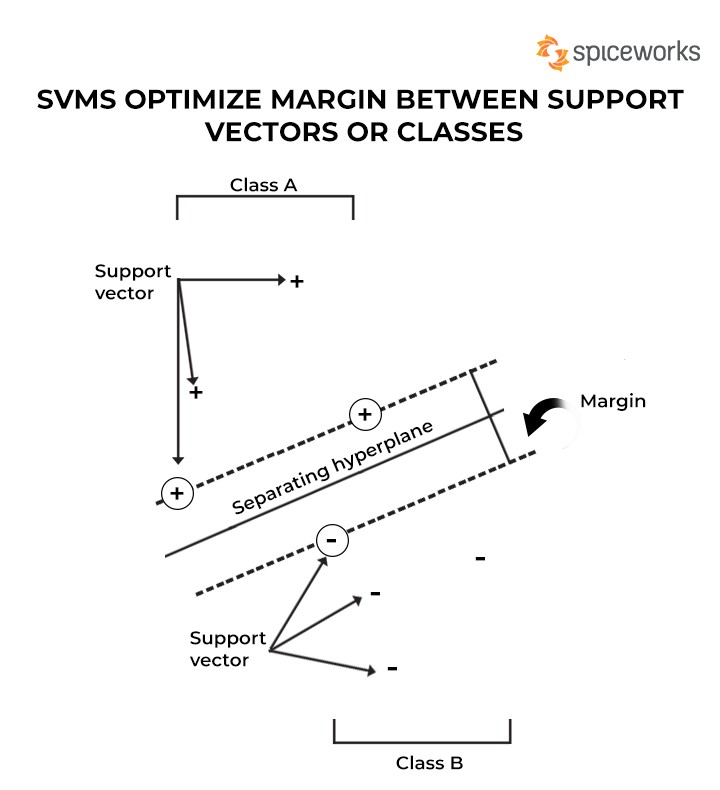SVM Classifications with Optimal Margin and Hyperplane

The primary goal of an SVM is to identify a hyperplane that distinctly separates data points of different classes. This hyperplane is strategically positioned to maximize the margin between the classes. In essence, the margin represents the widest possible slice parallel to the hyperplane, containing no internal support vectors. While defining such hyperplanes is straightforward for linearly separable problems, real-world scenarios often present challenges. In these cases, SVMs strive to maximize the margin between support vectors, which may lead to occasional misclassifications for smaller data point sections.

LEARNS.EDU.VN provides in-depth resources to help you understand and implement SVMs effectively.

SVMs are primarily designed for binary classification but can be adapted for multiclass problems. This adaptation involves constructing and combining multiple binary classifiers to achieve multiclass classifications through binary means. Mathematically, an SVM is a set of machine learning algorithms that use kernel methods to transform data features via kernel functions. These functions map complex datasets to higher dimensions, simplifying data point separation. The “kernel trick” allows efficient and inexpensive data transformation without fully transforming the data, which can be computationally taxing.

The concept of SVMs was first introduced in 1963 by Vladimir N. Vapnik and Alexey Ya. Chervonenkis. Since then, SVMs have gained immense popularity due to their wide-ranging applications in areas such as protein sorting, text categorization, facial recognition, autonomous vehicles, and robotic systems.

2. How Support Vector Machines Function

To better understand how a Support Vector Machine (SVM) operates, let’s walk through an illustrative example. Consider a dataset containing red and black labels, with corresponding features denoted by x and y. Our objective is to create a classifier that effectively categorizes this data into either the red or black category.

Imagine plotting this labeled data on an x-y plane. A typical SVM separates these data points into red and black categories using a hyperplane, which, in this instance, is a two-dimensional line. This hyperplane represents the decision boundary line, where data points fall under either the red or black category.

A hyperplane is defined as a line that maximizes the margins between the two closest labels (red and black). The distance from the hyperplane to the nearest label is maximized, simplifying data classification. This scenario applies to linearly separable data. However, for non-linear data, a simple straight line cannot separate distinct data points effectively.

Consider the following example of a non-linear complex dataset:

As the dataset illustrates, a single hyperplane is insufficient to separate the involved labels. However, the vectors are visibly distinct, making their segregation easier.

To classify this data, an additional dimension must be added to the feature space. For the linear data discussed earlier, two dimensions (x and y) were sufficient. In this case, we introduce a z-dimension to better classify the data points. For convenience, let’s use the equation for a circle: z = x² + y².

With the third dimension, the slice of feature space along the z-direction appears as follows:

Now, with three dimensions, the hyperplane runs parallel to the x-direction at a particular value of z; let’s assume z=1.

The remaining data points are then mapped back to two dimensions.

This figure illustrates the boundary for data points along features x, y, and z along a circle with a radius of 1 unit, segregating the two labels via the SVM.

Another method for visualizing data points in three dimensions involves separating two tags (such as two differently colored tennis balls). Imagine the balls lying on a 2D plane surface. If we lift the surface upward, all the tennis balls are distributed in the air. At a certain point, the two differently colored balls may separate. When this occurs, you can place the surface between the two segregated sets of balls.

In this process, “lifting” the 2D surface represents mapping data into higher dimensions, a technique known as “kernelling,” as mentioned earlier. Complex data points can be separated with the help of more dimensions. Data points continue to be mapped into higher dimensions until a hyperplane is identified that clearly separates them.

This concept is visualized in the following 3D use case:

LEARNS.EDU.VN offers comprehensive tutorials and resources to help you master these techniques. For example, consider attending our “Advanced Machine Learning Techniques” workshop, where you will gain hands-on experience with SVMs and other algorithms.

3. Types of Support Vector Machines

Support Vector Machines (SVMs) are broadly classified into two main types: simple or linear SVM and kernel or non-linear SVM.

3.1 Simple or Linear SVM

A linear SVM is used to classify linearly separable data. This means that if a dataset can be divided into categories or classes using a single straight line, it is termed a linear SVM, and the data is referred to as linearly distinct or separable. The classifier that classifies such data is known as a linear SVM classifier.

Simple SVMs are typically employed to address classification and regression analysis problems.

3.2 Kernel or Non-Linear SVM

Non-linear data, which cannot be segregated into distinct categories using a straight line, is classified using a kernel or non-linear SVM. The classifier, in this case, is referred to as a non-linear classifier. Classification can be performed with non-linear data by adding features into higher dimensions rather than relying on 2D space. The newly added features fit a hyperplane that helps easily separate classes or categories.

Kernel SVMs are typically used to handle optimization problems with multiple variables. At LEARNS.EDU.VN, you can find detailed courses that cover both linear and non-linear SVMs, equipping you with the skills to tackle various machine learning challenges.

4. Real-World Applications of Support Vector Machines

Support Vector Machines (SVMs) rely on supervised learning methods to classify unknown data into known categories, making them applicable in diverse fields. Here are some prominent real-world examples of SVMs:

4.1 Geo-Sounding Problem

The geo-sounding problem is a common application of SVMs, used to track the planet’s layered structure. This involves solving inversion problems where observations are used to factor in the variables that produced them. Linear functions and support vector algorithmic models separate the electromagnetic data. Linear programming practices are employed while developing supervised models. Given the relatively small problem size, the dimension size is inevitably tiny, which accounts for mapping the planet’s structure effectively.

4.2 Assessing Seismic Liquefaction Potential

Soil liquefaction is a significant concern during earthquakes. Assessing its potential is crucial for designing civil infrastructure. SVMs play a key role in determining the occurrence and non-occurrence of such liquefaction. SVMs handle two tests: the Standard Penetration Test (SPT) and the Cone Penetration Test (CPT), using field data to adjudicate the seismic status.

SVMs are also used to develop models involving multiple variables, such as soil factors and liquefaction parameters, to determine ground surface strength. SVMs can achieve an accuracy of close to 96-97% for these applications.

4.3 Protein Remote Homology Detection

Protein remote homology is a field in computational biology where proteins are categorized into structural and functional parameters based on their amino acid sequence, when sequence identification is difficult. SVMs play a key role in remote homology, with kernel functions determining commonalities between protein sequences. Thus, SVMs are vital in computational biology.

4.4 Data Classification

SVMs are known for solving complex mathematical problems, but smooth SVMs are preferred for data classification. Smoothing techniques reduce data outliers and make patterns identifiable. For optimization problems, smooth SVMs use algorithms like the Newton-Armijo algorithm to handle larger datasets that conventional SVMs cannot. Smooth SVM types explore mathematical properties such as strong convexity for more straightforward data classification, even with non-linear data.

4.5 Facial Detection and Expression Classification

SVMs classify facial structures versus non-facial ones. Training data uses two classes: face entity (+1) and non-face entity (-1), with n*n pixels to distinguish between face and non-face structures. Each pixel is analyzed, and features are extracted to denote face and non-face characteristics. The process creates a square decision boundary around facial structures based on pixel intensity and classifies the resultant images.

SVMs are also used for facial expression classification, including expressions like happy, sad, angry, and surprised.

4.6 Surface Texture Classification

SVMs are used to classify images of surfaces, determining and classifying the texture of surfaces as smooth or gritty.

4.7 Text Categorization and Handwriting Recognition

Text categorization involves classifying data into predefined categories, such as news articles (politics, business, stock market, sports) or emails (spam, non-spam, junk). Each article or document is assigned a score, which is then compared to a predefined threshold value. The article is classified into its respective category based on the evaluated score.

For handwriting recognition, datasets containing passages written by different individuals are supplied to SVMs. SVM classifiers are trained with sample data initially and later used to classify handwriting based on score values. SVMs are also used to segregate writings by humans and computers.

4.8 Speech Recognition

In speech recognition, words from speeches are individually picked and separated. For each word, certain features and characteristics are extracted using techniques like Mel Frequency Cepstral Coefficients (MFCC), Linear Prediction Coefficients (LPC), and Linear Prediction Cepstral Coefficients (LPCC). These methods collect audio data, feed it to SVMs, and train models for speech recognition.

4.9 Stenography Detection

SVMs can determine whether a digital image is tampered with, contaminated, or pure. This is helpful for security-related matters, as it is easier to encrypt and embed data as a watermark in high-resolution images. Such images contain more pixels, making it challenging to spot hidden messages. One solution is to separate each pixel and store data in different datasets that SVMs can later analyze.

4.10 Cancer Detection

Medical professionals use SVMs to detect cancer in its early stages. Cancerous images are supplied as input. SVM algorithms analyze them, train models, and categorize the images to reveal malign or benign cancer features. Google developed an AI tool in January 2020 to aid in early breast cancer detection and reduce false positives and negatives.

At LEARNS.EDU.VN, we provide advanced courses that dive deep into these applications, offering practical insights and hands-on experience.

5. Diving Deeper: Key Considerations for Implementing SVMs

Implementing Support Vector Machines (SVMs) effectively requires careful consideration of several key factors. These considerations can significantly impact the performance, accuracy, and applicability of SVM models in various real-world scenarios. Here, we delve into the critical aspects of SVM implementation, providing insights to optimize your machine-learning endeavors.

5.1 Hyperparameter Tuning

Hyperparameters are configuration settings that are external to the model and whose values cannot be estimated from data. These parameters must be set before the training process. For SVMs, key hyperparameters include:

• C (Regularization Parameter): This parameter controls the trade-off between achieving a low training error and minimizing the norm of the weights. A smaller C allows for a larger margin but may increase training error, leading to underfitting. Conversely, a larger C aims for lower training error, which can reduce the margin and potentially lead to overfitting.
• Kernel Type: The kernel function determines how data points are transformed to a higher dimensional space. Common kernel types include:
  • Linear: Suitable for linearly separable data.
  • Polynomial: Introduces polynomial features and is useful when data has polynomial relationships.
  • Radial Basis Function (RBF): A popular choice for non-linear data, controlled by the gamma parameter.
  • Sigmoid: Similar to a neural network’s activation function.
• Gamma (Kernel Coefficient): This parameter is specific to RBF, polynomial, and sigmoid kernels. It defines the influence of a single training example. A small gamma means a larger radius of influence, leading to more data points being considered when predicting a new point. A large gamma means a smaller radius, so predictions are based on points closer to the data point being predicted.
• Degree (Polynomial Kernel): This parameter specifies the degree of the polynomial kernel function and affects the model’s complexity.

Tuning Strategies:

• Grid Search: Exhaustively search a predefined subset of the hyperparameter space.
• Random Search: Randomly sample the hyperparameter space.
• Bayesian Optimization: Uses a probabilistic model to intelligently explore the hyperparameter space.

For example, using grid search, one might tune an SVM with an RBF kernel by varying C and gamma over a set of values like C = [0.1, 1, 10, 100] and gamma = [0.001, 0.01, 0.1, 1].

5.2 Kernel Selection

Choosing the appropriate kernel is crucial for SVM performance. The kernel function maps the input data into a higher-dimensional space, where it can perform linear separation. Here’s a guide:

• Linear Kernel:
  • Use Case: When the data is linearly separable or has a large number of features compared to the number of samples.
  • Advantages: Simple, computationally efficient, and requires less tuning.
  • Disadvantages: Not suitable for complex non-linear relationships.
• Polynomial Kernel:
  • Use Case: When the data has polynomial relationships.
  • Advantages: Can handle non-linear data and model complex interactions.
  • Disadvantages: Requires tuning the degree parameter and can be computationally expensive.
• RBF Kernel:
  • Use Case: When the data has non-linear relationships and no prior knowledge about its structure.
  • Advantages: Very flexible, can handle complex non-linear data, and often performs well in various applications.
  • Disadvantages: Requires tuning the gamma parameter and can be sensitive to hyperparameter choices.
• Sigmoid Kernel:
  • Use Case: Similar to neural networks, but less commonly used.
  • Advantages: Can sometimes perform well with certain types of data.
  • Disadvantages: Not as versatile as RBF and can sometimes behave like a linear kernel.

For example, if you’re working on image classification and suspect that the features have non-linear relationships, the RBF kernel is a good starting point.

5.3 Handling Non-Linear Data

Real-world data is often non-linear and cannot be easily separated by a linear hyperplane. SVMs address this issue through the kernel trick, which implicitly maps data into a higher-dimensional space without explicitly computing the transformation. This allows the SVM to find a linear hyperplane in the higher-dimensional space that corresponds to a non-linear boundary in the original space.

Strategies:

• Kernel Trick: Using kernel functions like RBF or polynomial to map data to higher dimensions.
• Feature Engineering: Manually creating new features that capture non-linear relationships in the data.
• Data Transformation: Applying transformations such as logarithmic or exponential scaling to make data more amenable to linear separation.

For instance, consider data where classes are separated by a circular boundary. Using the RBF kernel, the SVM can effectively learn this boundary without requiring explicit feature engineering.

5.4 Dealing with Imbalanced Datasets

Imbalanced datasets, where one class significantly outnumbers the other, can pose challenges for SVMs. The model may be biased towards the majority class, resulting in poor performance on the minority class.

Strategies:

• Class Weights: Adjust the class_weight parameter in the SVM to give higher weight to the minority class.
• Oversampling: Increase the number of minority class samples using techniques like SMOTE (Synthetic Minority Oversampling Technique).
• Undersampling: Reduce the number of majority class samples.

For example, if you have a fraud detection dataset where fraudulent transactions are rare, you can use class weights to penalize misclassifications of the minority class more heavily.

5.5 Scalability and Computational Complexity

SVMs can be computationally intensive, especially with large datasets. The training time complexity is roughly between O(n^2) and O(n^3), where n is the number of samples.

Strategies:

• Mini-Batch Training: Training the SVM on smaller subsets of data.
• Approximation Methods: Using approximation techniques to reduce the computational cost.
• Feature Selection: Reducing the number of features to decrease the dimensionality of the data.

5.6 Performance Evaluation

Evaluating the performance of an SVM model is essential to ensure it generalizes well to unseen data. Key metrics include:

• Accuracy: Overall correctness of the model.
• Precision: Ability of the model to avoid false positives.
• Recall: Ability of the model to capture all positive instances.
• F1-Score: Harmonic mean of precision and recall.
• AUC-ROC: Area under the Receiver Operating Characteristic curve, which measures the model’s ability to discriminate between classes.

For example, in a medical diagnosis application, high recall is critical to ensure that as many true positive cases as possible are identified, even if it means accepting some false positives.

5.7 Cross-Validation

Cross-validation is a technique used to assess how well a model generalizes to an independent dataset. It involves partitioning the data into multiple subsets, training the model on some subsets, and evaluating it on the remaining subsets.

Strategies:

• K-Fold Cross-Validation: Partition the data into k subsets, training the model on k-1 subsets and evaluating it on the remaining subset, repeating this process k times.
• Stratified K-Fold Cross-Validation: Similar to k-fold, but ensures that each fold contains the same proportion of classes as the original dataset.

For example, using 5-fold cross-validation, you would train and evaluate the SVM five times, each time using a different 20% of the data as a validation set.

5.8 Handling Noisy Data

Noisy data, which contains irrelevant or meaningless information, can negatively impact the performance of SVMs.

Strategies:

• Data Cleaning: Removing or correcting noisy data points.
• Robust Kernels: Using kernels that are less sensitive to outliers, such as the Laplacian kernel.
• Regularization: Increasing the regularization parameter C to reduce the impact of noisy data points.

For instance, if you’re working with sensor data that contains occasional erroneous readings, data cleaning and robust kernels can help improve the SVM’s performance.

5.9 Feature Scaling

Feature scaling is essential to ensure that all features contribute equally to the model. SVMs are sensitive to the scale of input features, and features with larger values can dominate the learning process.

Strategies:

• Standardization: Scaling features to have zero mean and unit variance.
• Min-Max Scaling: Scaling features to a fixed range, typically between 0 and 1.

For example, if one feature represents age (ranging from 0 to 100) and another represents income (ranging from 0 to 1,000,000), scaling ensures that income does not dominate the learning process due to its larger values.

5.10 Regularization Techniques

Regularization is used to prevent overfitting, which occurs when the model learns the training data too well and performs poorly on unseen data.

Strategies:

• L1 Regularization: Adds a penalty term proportional to the absolute value of the weights. This can lead to sparse solutions, where some weights are exactly zero, effectively performing feature selection.
• L2 Regularization: Adds a penalty term proportional to the square of the weights. This encourages smaller weights and can improve the model’s generalization performance.

For example, using L2 regularization, the SVM aims to find a decision boundary that not only separates the classes well but also has smaller weights, reducing the risk of overfitting.

By carefully considering these factors, you can effectively implement Support Vector Machines and achieve optimal performance in your machine learning applications.

At LEARNS.EDU.VN, we offer comprehensive resources to guide you through these advanced topics. Our “Advanced Machine Learning Algorithms” course provides in-depth knowledge and practical exercises to master SVMs.

6. Educational Resources at LEARNS.EDU.VN

At LEARNS.EDU.VN, we are dedicated to providing comprehensive educational resources that empower learners of all levels to excel in machine learning and data science. Our platform offers a wide array of content, from foundational concepts to advanced techniques, ensuring you have the knowledge and skills needed to succeed in today’s data-driven world.

6.1 Structured Courses

Our structured courses are designed to provide a step-by-step learning experience, covering all essential aspects of machine learning, including Support Vector Machines (SVMs). Each course is crafted by industry experts and educators to ensure relevance and accuracy.

Introduction to Machine Learning

• Target Audience: Beginners with little to no background in machine learning.
• Course Outline:
  • Overview of Machine Learning: Types, applications, and ethical considerations.
  • Data Preprocessing: Cleaning, transforming, and preparing data for modeling.
  • Supervised Learning: Linear regression, logistic regression, decision trees, and SVMs.
  • Unsupervised Learning: Clustering techniques (K-Means, hierarchical clustering), dimensionality reduction (PCA).
  • Model Evaluation: Metrics, cross-validation, and hyperparameter tuning.

Advanced Machine Learning Algorithms

• Target Audience: Learners with a foundational understanding of machine learning who want to delve deeper into advanced algorithms.
• Course Outline:
  • Support Vector Machines (SVMs): Kernel methods, hyperparameter tuning, and applications.
  • Ensemble Methods: Random forests, gradient boosting, and AdaBoost.
  • Neural Networks: Deep learning architectures, backpropagation, and convolutional neural networks (CNNs).
  • Bayesian Methods: Gaussian processes and Bayesian optimization.
  • Time Series Analysis: ARIMA models, forecasting techniques.

Practical Machine Learning with Python

• Target Audience: Learners who want to gain hands-on experience implementing machine learning models using Python.
• Course Outline:
  • Python Libraries for Machine Learning: NumPy, pandas, scikit-learn.
  • Data Visualization: Matplotlib and seaborn.
  • Implementing Supervised Learning Algorithms: Linear regression, logistic regression, SVMs, and ensemble methods.
  • Implementing Unsupervised Learning Algorithms: Clustering and dimensionality reduction.
  • Case Studies: Real-world machine learning projects.

6.2 Detailed Tutorials

Our detailed tutorials offer in-depth explanations and step-by-step guides on specific topics, allowing you to focus on areas of particular interest. These tutorials are designed to be accessible and easy to follow, regardless of your technical background.

• Understanding SVM Kernels: This tutorial provides a comprehensive overview of different kernel functions and how to choose the right one for your data.
• Hyperparameter Tuning for SVMs: Learn how to optimize SVM performance using techniques like grid search and cross-validation.
• SVMs for Imbalanced Datasets: Discover strategies for handling imbalanced data and improving model performance on minority classes.
• Implementing SVMs with scikit-learn: A practical guide to using scikit-learn to build and train SVM models.

6.3 Practice Exercises

Reinforce your learning with our practice exercises, designed to test your understanding and build your skills. These exercises range from simple quizzes to complex coding challenges.

• Multiple Choice Quizzes: Test your knowledge of key concepts and terminology.
• Coding Challenges: Implement machine learning algorithms from scratch and apply them to real-world datasets.
• Case Studies: Analyze and solve real-world machine learning problems using the techniques you’ve learned.

6.4 Expert Insights

Benefit from the knowledge and experience of industry experts through our expert insights section. This includes articles, interviews, and webinars featuring leading professionals in the field.

• Articles: Gain insights into the latest trends and developments in machine learning.
• Interviews: Learn from experts about their experiences, challenges, and successes in the field.
• Webinars: Attend live sessions and Q&A sessions with industry leaders.

6.5 Community Forums

Connect with other learners and experts in our community forums. Share your knowledge, ask questions, and collaborate on projects.

• Discussion Boards: Discuss course content, ask questions, and share your insights.
• Project Collaboration: Find partners for your machine learning projects.
• Networking: Connect with other professionals in the field.

6.6 Personalized Learning Paths

Customize your learning experience with our personalized learning paths. These paths are tailored to your individual goals and interests, ensuring you get the most out of your learning journey.

• Career Paths: Choose a career path, such as data scientist or machine learning engineer, and receive a curated set of courses and resources to help you achieve your goals.
• Skill Paths: Focus on developing specific skills, such as model evaluation or hyperparameter tuning.
• Project-Based Learning: Learn by doing, with hands-on projects that allow you to apply your knowledge to real-world problems.

7. The Power of LEARNS.EDU.VN: Enhancing Your Learning Experience

At LEARNS.EDU.VN, we understand the challenges learners face in finding reliable and high-quality educational resources. That’s why we are committed to providing comprehensive support and guidance to help you achieve your learning goals. Our platform is designed to make learning accessible, engaging, and effective, ensuring you gain the knowledge and skills needed to succeed.

7.1 Addressing Common Challenges

• Difficulty Finding Quality Resources: We curate and create high-quality educational content, ensuring you have access to accurate and up-to-date information.
• Lack of Motivation: Our engaging and interactive learning materials keep you motivated and inspired throughout your learning journey.
• Complex Concepts: We break down complex concepts into simple, easy-to-understand explanations, making learning more accessible.
• Ineffective Learning Methods: We provide proven learning methods, such as practice exercises and project-based learning, to help you retain and apply your knowledge.
• Knowing Where to Start: Our personalized learning paths guide you through the learning process, ensuring you know exactly what to learn and when.

7.2 Services Provided

• Detailed Guides: We offer detailed guides on various topics, providing step-by-step instructions and clear explanations.
• Effective Learning Methods: We share proven learning methods to help you maximize your learning potential.
• Simplified Explanations: We simplify complex concepts, making them easier to understand.
• Clear Learning Paths: We provide clear learning paths, guiding you through your learning journey.
• Useful Resources: We introduce you to useful resources, such as tools and applications, to support your learning.
• Expert Connections: We connect you with educational experts, providing you with personalized guidance and support.

8. Frequently Asked Questions (FAQ) about Support Vector Machines

Q1: What is a Support Vector Machine (SVM)?

A Support Vector Machine (SVM) is a supervised machine learning algorithm used for classification, regression, and outlier detection. It works by finding an optimal hyperplane that separates data points into different classes with the largest possible margin.

Q2: What are the key components of an SVM?

Key components include:

• Hyperplane: The decision boundary that separates the classes.
• Support Vectors: Data points closest to the hyperplane that influence its position and orientation.
• Margin: The distance between the hyperplane and the nearest data points (support vectors) from each class.

Q3: What is the difference between linear and non-linear SVM?

• Linear SVM: Used when the data is linearly separable, meaning it can be separated by a straight line (in 2D) or a hyperplane (in higher dimensions).
• Non-Linear SVM: Used when the data is not linearly separable. It employs kernel functions to map the data into a higher-dimensional space where it can be linearly separated.

Q4: What are kernel functions in SVM?

Kernel functions are mathematical functions that transform data into a higher-dimensional space, allowing SVMs to perform non-linear classification or regression. Common kernel functions include:

• Linear Kernel: Suitable for linearly separable data.
• Polynomial Kernel: Introduces polynomial features.
• Radial Basis Function (RBF) Kernel: A versatile kernel for non-linear data.
• Sigmoid Kernel: Similar to a neural network’s activation function.

Q5: How do I choose the right kernel function for my SVM model?

The choice of kernel function depends on the nature of the data. If the data is linearly separable, a linear kernel is sufficient. For non-linear data, RBF is often a good starting point due to its flexibility. However, polynomial and sigmoid kernels can also be used depending on the specific problem.

Q6: What is the regularization parameter ‘C’ in SVM?

The regularization parameter C controls the trade-off between achieving a low training error and maximizing the margin. A smaller C allows for a larger margin but may increase training error, leading to underfitting. A larger C aims for lower training error, which can reduce the margin and potentially lead to overfitting.

Q7: How does SVM handle imbalanced datasets?

SVM can handle imbalanced datasets using techniques like:

• Class Weights: Adjusting the class_weight parameter to give higher weight to the minority class.
• Oversampling: Increasing the number of minority class samples using techniques like SMOTE.
• Undersampling: Reducing the number of majority class samples.

Q8: What are the advantages of using SVM?

Advantages of SVM include:

• Effective in high-dimensional spaces.
• Relatively memory efficient.
• Versatile due to different Kernel functions.
• Effective for both linearly and non-linearly separable data.

Q9: What are the disadvantages of using SVM?

Disadvantages of SVM include:

• Can be computationally intensive, especially with large datasets.
• Sensitive to the choice of kernel function and hyperparameters.
• Difficult to interpret for complex models.

Q10: Where can I learn more about Support Vector Machines?

You can learn more about Support Vector Machines at LEARNS.EDU.VN. We offer structured courses, detailed tutorials, practice exercises, and expert insights to help you master SVMs and other machine learning techniques. Visit our website at LEARNS.EDU.VN or contact us at +1 555-555-1212 for more information. Our address is 123 Education Way, Learnville, CA 90210, United States.

9. Unlock Your Potential with LEARNS.EDU.VN

Are you ready to take your learning to the next level? Visit LEARNS.EDU.VN today and discover a wealth of educational resources that can help you achieve your goals. Whether you’re looking to learn a new skill, understand a complex concept, or find effective learning methods, LEARNS.EDU.VN has something for everyone. Don’t wait – start your learning journey today!

At LEARNS.EDU.VN, we are committed to providing the best possible learning experience. Join our community of learners and discover the power of education. For more information, visit our website or contact us using the information below:

• Address: 123 Education Way, Learnville, CA 90210, United States
• WhatsApp: +1 555-555-1212
• Website: learns.edu.vn

We look forward to helping you achieve your learning goals!