Are you curious about what your child will learn in 3rd grade math? LEARNS.EDU.VN offers a comprehensive overview, making complex math concepts easy to grasp. Discover how multiplication, division, fractions, and more become accessible through practical examples and visual aids. Empower your child’s learning journey with us. Dive in and explore key math skills, problem-solving strategies, and real-world applications for 3rd graders. This knowledge prepares them for standardized tests and builds a solid mathematical foundation.
1. Mastering Multiplication and Division Facts
Third grade marks a significant leap in mathematical understanding as students delve into the world of multiplication and division. This isn’t just about memorizing facts; it’s about understanding the underlying concepts. Students will learn to visualize multiplication as repeated addition and division as sharing or grouping. They’ll explore multiplication tables, learn strategies for remembering facts, and discover the relationship between multiplication and division.
- Multiplication: Understanding that 3 x 4 is the same as adding 3 four times (3 + 3 + 3 + 3).
- Division: Grasping that 12 ÷ 3 means dividing 12 objects into 3 equal groups.
1.1. Building a Foundation with Visual Aids
To make multiplication and division more concrete, teachers often use visual aids like arrays (arranging objects in rows and columns) and number lines. These tools help children see the patterns and relationships within multiplication and division. Manipulatives like counters or blocks can also be invaluable for hands-on learning.
For instance, students can use counters to create an array representing 4 x 6. By arranging 4 rows of 6 counters, they can visually see the product is 24.
1.2. Strategies for Memorizing Multiplication Facts
Memorizing multiplication facts can be challenging, but there are strategies to make it easier. Some popular methods include:
- Chanting: Reciting multiplication facts aloud can help with memorization.
- Flashcards: Using flashcards for quick recall practice.
- Games: Playing multiplication games can make learning fun and engaging.
1.3. Real-World Applications of Multiplication and Division
Connecting multiplication and division to real-world scenarios helps students understand their relevance. Examples include:
- Sharing equally: Dividing a pizza into equal slices for friends.
- Calculating costs: Multiplying the price of an item by the quantity purchased.
- Measuring ingredients: Doubling or tripling a recipe using multiplication.
Providing these practical examples helps students see that math isn’t just an abstract concept but a useful tool in everyday life.
2. Understanding the Inverse Relationship
A critical concept in third grade math is understanding the inverse relationship between multiplication and division. This means recognizing that one operation can “undo” the other. Just as addition and subtraction are inverse operations, multiplication and division share this connection.
2.1. Exploring Fact Families
Fact families are a great way to illustrate the inverse relationship. A fact family consists of four related facts using the same three numbers. For example, the fact family for 3, 4, and 12 includes:
- 3 x 4 = 12
- 4 x 3 = 12
- 12 ÷ 3 = 4
- 12 ÷ 4 = 3
By exploring fact families, students can see how multiplication and division are interconnected.
2.2. Using Multiplication to Check Division
Understanding the inverse relationship allows students to use multiplication to check their division answers. If a student divides 20 by 5 and gets 4, they can multiply 5 by 4 to verify the answer. If the product is 20, the division is correct.
2.3. Applying the Concept to Problem-Solving
The inverse relationship is also essential for solving word problems. For example, if a problem states that “John has 24 cookies and wants to share them equally among 6 friends,” students can use division to find the answer (24 ÷ 6 = 4). Alternatively, they can think, “What number multiplied by 6 equals 24?” This reinforces the connection between the two operations.
 Multiplication table and chart to learn multiplication
Multiplication table and chart to learn multiplication
3. Mastering Word Problems with Four Operations
Third graders are expected to tackle word problems that require using all four operations: addition, subtraction, multiplication, and division. These problems often involve multiple steps and require students to carefully analyze the information provided.
3.1. Strategies for Solving Word Problems
Several strategies can help students approach word problems effectively:
- Read the problem carefully: Understand what the problem is asking.
- Identify key information: Look for numbers and keywords that indicate which operations to use (e.g., “in all” suggests addition, “difference” suggests subtraction).
- Draw a picture or diagram: Visualizing the problem can help in understanding.
- Write a number sentence: Translate the problem into a mathematical equation.
- Solve the equation: Perform the necessary calculations.
- Check the answer: Make sure the answer makes sense in the context of the problem.
3.2. Recognizing Keywords and Their Operations
Certain keywords often indicate which operation to use:
| Keyword | Operation | Example |
|---|---|---|
| In all | Addition | “How many apples are there in all if you have 5 red apples and 3 green apples?” |
| Difference | Subtraction | “What is the difference between 10 and 4?” |
| Product | Multiplication | “What is the product of 6 and 7?” |
| Quotient | Division | “What is the quotient of 24 divided by 8?” |
3.3. Tackling Two-Step Problems
Two-step problems require students to perform two operations in order to find the solution. These problems can be more challenging but help develop critical thinking skills. For example:
“Sarah has 15 stickers. She gives 3 stickers to each of her 4 friends. How many stickers does Sarah have left?”
- Step 1: Multiply 3 stickers by 4 friends (3 x 4 = 12).
- Step 2: Subtract 12 stickers from 15 stickers (15 – 12 = 3).
Therefore, Sarah has 3 stickers left.
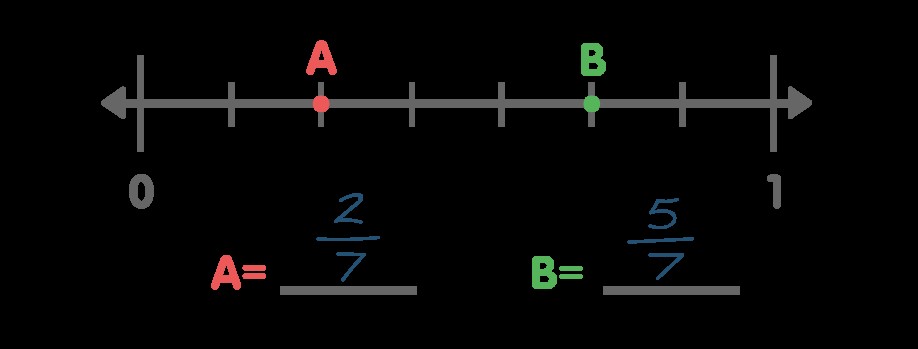
4. Diving Into Fractions on a Number Line
Third grade is when students start to deepen their understanding of fractions. They learn to represent fractions on a number line and compare different fractions. This visual representation helps them grasp the concept of fractions as parts of a whole.
4.1. Representing Fractions on a Number Line
A number line is a powerful tool for visualizing fractions. To represent a fraction on a number line, students need to:
- Draw a number line from 0 to 1.
- Divide the number line into equal parts, according to the denominator of the fraction.
- Mark the fraction on the number line, according to the numerator.
For example, to represent 1/4 on a number line, divide the line from 0 to 1 into 4 equal parts and mark the first part as 1/4.
4.2. Comparing Fractions
Number lines can also be used to compare fractions. By plotting different fractions on the same number line, students can visually see which fraction is larger or smaller.
For example, to compare 1/2 and 1/4, plot both fractions on a number line. Students will see that 1/2 is further to the right, indicating that it is larger than 1/4.
4.3. Equivalent Fractions
Third graders also learn about equivalent fractions, which are fractions that represent the same value. Number lines can help demonstrate this concept. For example, by dividing a number line into halves and then into fourths, students can see that 1/2 is equivalent to 2/4.
5. Telling Time to the Minute
Mastering time-telling is a crucial life skill. In third grade, students move beyond telling time to the nearest five minutes and learn to tell time to the minute. This requires a deeper understanding of how an analog clock works.
5.1. Understanding the Parts of an Analog Clock
An analog clock has two hands:
- Hour hand: The shorter hand that indicates the hour.
- Minute hand: The longer hand that indicates the minutes.
Students need to understand that the hour hand moves slowly throughout the hour, while the minute hand moves more quickly.
5.2. Reading the Minute Hand
Each number on an analog clock represents 5 minutes. To tell time to the minute, students need to count the minutes between the numbers. For example, if the minute hand is pointing at the 3, it represents 15 minutes. If it’s slightly past the 3, students need to count the additional minutes.
5.3. Practical Activities for Learning Time
Making time-telling practice interactive can be very effective. Some activities include:
- Using a real clock: Practice telling time throughout the day.
- Setting alarms: Have students set alarms for specific times.
- Creating a schedule: Make a daily schedule and have students track the time.
6. Creating Scaled Bar and Picture Graphs
In third grade, students learn how to create and interpret scaled bar and picture graphs. This means that each picture or bar can represent more than one unit. This skill is essential for data analysis and interpretation.
6.1. Understanding Scaled Graphs
A scaled graph uses a scale to represent data in a more compact way. For example, instead of using one picture to represent one item, a picture could represent 5 items. This is particularly useful when dealing with large numbers.
6.2. Creating Scaled Picture Graphs
To create a scaled picture graph:
- Collect data: Gather information on the topic.
- Choose a scale: Determine how many items each picture will represent.
- Draw the pictures: Represent the data using the chosen scale.
- Label the graph: Add a title and labels for the axes.
For example, if a graph shows the number of books read by students, and each picture of a book represents 2 books, a student who read 10 books would be represented by 5 book pictures.
6.3. Creating Scaled Bar Graphs
To create a scaled bar graph:
- Collect data: Gather information on the topic.
- Choose a scale: Determine the interval for the vertical axis.
- Draw the bars: Represent the data using bars of appropriate length.
- Label the graph: Add a title and labels for the axes.
For example, if a graph shows the number of students who like different colors, and the scale is 1 unit = 5 students, a bar that reaches the 4 mark would represent 20 students.
6.4. Interpreting Scaled Graphs
Interpreting scaled graphs involves reading the data and understanding the scale. Students need to be able to answer questions like:
- What is the total number of items represented in the graph?
- Which category has the most items?
- What is the difference between two categories?
7. Exploring Area and Perimeter
Third graders are introduced to the concepts of area and perimeter. These are fundamental concepts in geometry and have practical applications in everyday life.
7.1. Understanding Area
Area is the amount of space inside a two-dimensional shape. It is measured in square units (e.g., square inches, square centimeters).
To find the area of a rectangle or square, students learn the formula:
- Area = Length x Width
For example, if a rectangle has a length of 5 inches and a width of 3 inches, its area is 5 x 3 = 15 square inches.
7.2. Understanding Perimeter
Perimeter is the total distance around the outside of a two-dimensional shape. It is measured in linear units (e.g., inches, centimeters).
To find the perimeter of a rectangle or square, students learn the formula:
- Perimeter = 2 x (Length + Width)
For example, if a rectangle has a length of 5 inches and a width of 3 inches, its perimeter is 2 x (5 + 3) = 16 inches.
7.3. Differentiating Between Area and Perimeter
It’s important for students to understand the difference between area and perimeter. Area measures the space inside a shape, while perimeter measures the distance around it. Using manipulatives like tiles or blocks can help students visualize these concepts.
7.4. Real-World Applications of Area and Perimeter
Connecting area and perimeter to real-world examples helps students see their relevance:
- Area: Calculating the amount of carpet needed to cover a floor.
- Perimeter: Determining the amount of fencing needed to enclose a garden.
8. Key Mathematical Vocabulary
To succeed in third grade math, students need to learn and understand key mathematical vocabulary. These terms help them communicate effectively and understand complex concepts.
8.1. Essential Vocabulary List
Here is a list of essential math vocabulary for third graders:
| Term | Definition | Example |
|---|---|---|
| Multiplication | The process of repeated addition. | 3 x 4 = 12 (3 multiplied by 4 equals 12) |
| Division | The process of splitting a quantity into equal groups. | 12 ÷ 3 = 4 (12 divided by 3 equals 4) |
| Fraction | A part of a whole. | 1/2 (one-half) |
| Numerator | The top number in a fraction, indicating the number of parts being considered. | In 1/4, the numerator is 1. |
| Denominator | The bottom number in a fraction, indicating the total number of parts. | In 1/4, the denominator is 4. |
| Area | The amount of space inside a two-dimensional shape. | The area of a rectangle is length x width. |
| Perimeter | The total distance around the outside of a two-dimensional shape. | The perimeter of a square is 4 times the length of one side. |
| Product | The result of multiplication. | The product of 5 and 6 is 30. |
| Quotient | The result of division. | The quotient of 20 divided by 4 is 5. |
| Equivalent | Having the same value. | 1/2 and 2/4 are equivalent fractions. |
| Number Line | A line on which numbers are marked at intervals. | Used to visualize fractions, decimals, and whole numbers. |
| Bar Graph | A graph that uses bars to represent data. | Used to compare quantities or values. |
| Picture Graph | A graph that uses pictures to represent data. | Used to show data in a visually appealing way. |
| Scale | A set of numbers that represent data in a graph. | A scale of 1 unit = 5 items on a bar graph. |
| Word Problem | A math problem presented in the form of a story or scenario. | Requires understanding and applying mathematical concepts to solve. |
| Operation | A mathematical process, such as addition, subtraction, multiplication, or division. | Used to perform calculations and solve problems. |
| Inverse Operation | An operation that undoes another operation. | Addition and subtraction are inverse operations; multiplication and division. |
8.2. Activities to Reinforce Vocabulary
To help students learn and retain mathematical vocabulary, try these activities:
- Vocabulary games: Play games like Math Bingo or Pictionary using math terms.
- Word walls: Create a word wall with definitions and examples of key terms.
- Flashcards: Use flashcards for quick recall practice.
- Sentence writing: Have students write sentences using the vocabulary words in context.
By focusing on mathematical vocabulary, you can empower students to communicate effectively and build a strong foundation for future math learning.
9. Advanced Concepts for 3rd Grade Math
While the core curriculum focuses on the topics mentioned above, some advanced concepts can be introduced to challenge high-achieving students.
9.1. Introduction to Geometry
Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogs.
Third graders can be introduced to basic geometric shapes like:
- Triangles: 3-sided polygons
- Squares: 4-sided polygons with equal sides and right angles
- Rectangles: 4-sided polygons with opposite sides equal and right angles
- Circles: A round plane figure whose boundary consists of points equidistant from the center
They can also learn about concepts like symmetry, congruence, and similarity.
9.2. Understanding Decimals
Decimals are another way to represent parts of a whole. Third graders can be introduced to basic decimals like tenths and hundredths. They can learn to represent decimals on a number line and compare different decimals.
For example, 0.5 is equivalent to 1/2, and 0.25 is equivalent to 1/4.
9.3. Introduction to Measurement
Measurement involves determining the size, quantity, or extent of something. Third graders can learn about different units of measurement, such as:
- Length: Inches, feet, centimeters, meters
- Weight: Ounces, pounds, grams, kilograms
- Volume: Cups, pints, quarts, liters
They can also learn to convert between different units of measurement.
10. Making Math Fun and Engaging
Learning math doesn’t have to be a chore. There are many ways to make math fun and engaging for third graders.
10.1. Using Games
Math games can make learning more interactive and enjoyable. Some popular games include:
- Math Bingo: A fun way to practice math facts.
- Math Puzzles: Puzzles that require problem-solving skills.
- Online Math Games: Many websites offer engaging math games for third graders.
10.2. Incorporating Real-World Examples
Connecting math to real-world scenarios helps students see its relevance. Examples include:
- Cooking: Measuring ingredients and doubling recipes.
- Shopping: Calculating discounts and figuring out the total cost.
- Building: Measuring lengths and calculating areas.
10.3. Encouraging Exploration and Discovery
Encourage students to explore math concepts on their own. Let them experiment with manipulatives, draw pictures, and come up with their own strategies for solving problems.
FAQ Section
Q1: What are the main math topics covered in 3rd grade?
A1: Third grade math primarily covers multiplication and division, fractions, telling time to the minute, creating graphs, and understanding area and perimeter.
Q2: How can I help my child with multiplication facts?
A2: Use flashcards, chanting, and games to help your child memorize multiplication facts. Real-world examples can also make it more relatable.
Q3: What strategies can help my child solve word problems?
A3: Encourage your child to read the problem carefully, identify key information, draw a picture, write a number sentence, and check the answer.
Q4: How can I make learning fractions easier for my child?
A4: Use visual aids like number lines and manipulatives to help your child understand fractions. Real-world examples like sharing a pizza can also be helpful.
Q5: What is the difference between area and perimeter?
A5: Area measures the space inside a shape, while perimeter measures the distance around it. Use manipulatives like tiles or blocks to help your child visualize these concepts.
Q6: What are scaled bar and picture graphs?
A6: Scaled graphs use a scale to represent data in a more compact way. Each picture or bar can represent more than one unit.
Q7: How can I help my child learn to tell time to the minute?
A7: Use a real clock, set alarms, and create a schedule to help your child practice telling time.
Q8: What should I do if my child is struggling with math?
A8: Identify the specific areas where your child is struggling and provide additional support. Consider using online resources or working with a tutor.
Q9: Are there any advanced math concepts for 3rd graders?
A9: Yes, some advanced concepts include geometry, decimals, and measurement. These can be introduced to challenge high-achieving students.
Q10: How can I make math more fun and engaging for my child?
A10: Use games, incorporate real-world examples, and encourage exploration and discovery to make math more enjoyable.
Conclusion
Third grade math is a crucial year for building a strong foundation in mathematics. By understanding the key topics and using effective strategies, you can support your child’s learning journey and help them succeed. LEARNS.EDU.VN offers a wealth of resources and tools to further enhance your child’s math skills. From in-depth articles to interactive exercises, we provide the support you need to make math engaging and accessible. Take the next step in your child’s education and explore the resources available at LEARNS.EDU.VN today. Contact us at 123 Education Way, Learnville, CA 90210, United States, Whatsapp: +1 555-555-1212, or visit our website at learns.edu.vn.