What Do You Learn In Algebra? Algebra, a cornerstone of mathematics, unveils a world of problem-solving and analytical thinking. This guide, brought to you by LEARNS.EDU.VN, will illuminate the core concepts of algebra and demonstrate its relevance to various fields, paving the way for your mathematical journey. Discover the fundamentals of algebraic manipulation and unlock the power of equations and expressions.
Table of Contents
- Understanding Algebra’s Core Principles
- Key Topics Covered in Algebra
- Essential Laws Governing Algebra
- Fundamental Formulas in Algebra
- Algebra 1 vs. Algebra 2: Key Differences
- Strategies and Tips for Mastering Algebra
- Real-World Applications of Algebra
- The Importance of Algebra in Higher Education
- Common Challenges in Learning Algebra and How to Overcome Them
- Leveraging LEARNS.EDU.VN for Algebra Success
- Advanced Algebraic Concepts and Their Applications
- Algebra and Technology: Tools for Success
- Algebra in Standardized Tests: What to Expect
- Future Trends in Algebra Education
- Frequently Asked Questions About Algebra
1. Understanding Algebra’s Core Principles
Algebra is a branch of mathematics that uses symbols and letters to represent numbers and quantities in formulas and equations. It extends the basic arithmetic operations to a more general context, allowing us to solve for unknown values and explore relationships between different quantities. The core principle of algebra lies in its ability to abstract mathematical concepts, making it a powerful tool for modeling and solving problems across various disciplines. It’s not just about manipulating symbols; it’s about understanding the underlying logic and structure of mathematical relationships. According to the National Council of Teachers of Mathematics (NCTM), algebra is essential for developing critical thinking and problem-solving skills.
1.1 The Essence of Algebraic Thinking
Algebraic thinking involves more than just performing calculations; it’s about understanding patterns, relationships, and functions. It enables you to analyze situations, identify variables, and create equations to represent real-world scenarios. This form of thinking is crucial for success in higher-level mathematics and various STEM fields. Algebraic thinking allows you to move beyond rote memorization and develop a deeper understanding of mathematical concepts. A study by the University of California, Berkeley, found that students who develop strong algebraic thinking skills perform better in all areas of mathematics.
1.2 The Language of Algebra: Variables, Constants, and Expressions
Algebra uses specific vocabulary to convey mathematical ideas precisely. Key terms include:
- Variables: Symbols (usually letters) representing unknown values.
- Constants: Fixed numerical values that do not change.
- Expressions: Combinations of variables, constants, and mathematical operations.
- Equations: Statements that show the equality between two expressions.
Understanding these terms is essential for reading, interpreting, and manipulating algebraic equations. Mastering the language of algebra is like learning the grammar of a new language; it allows you to communicate mathematical ideas effectively and accurately.
1.3 Real Numbers and Their Properties
Algebra builds upon the foundation of real numbers, which include rational and irrational numbers. Understanding the properties of real numbers, such as the commutative, associative, and distributive properties, is crucial for simplifying and solving algebraic equations. These properties provide the rules for manipulating numbers and expressions in a consistent and logical manner.
2. Key Topics Covered in Algebra
Algebra encompasses a wide range of topics, each building upon the previous ones. These topics provide a comprehensive understanding of algebraic principles and their applications. From basic equations to complex functions, algebra equips you with the tools to solve a variety of mathematical problems.
2.1 Linear Equations and Inequalities
Linear equations are algebraic expressions in which the highest power of the variable is one. Solving linear equations involves isolating the variable to find its value. Linear inequalities are similar to linear equations but use inequality symbols (>, <, ≥, ≤) to compare expressions.
Example: 2x + 3 = 7 (Linear Equation), 3x – 5 > 4 (Linear Inequality)
2.2 Systems of Linear Equations
A system of linear equations involves two or more linear equations with the same variables. Solving these systems involves finding the values of the variables that satisfy all equations simultaneously. Common methods for solving systems of linear equations include substitution, elimination, and graphing.
Example:
- 2x + y = 5
- x – y = 1
2.3 Polynomials and Factoring
Polynomials are algebraic expressions that consist of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Factoring involves breaking down a polynomial into simpler expressions. Polynomials are the building blocks of more advanced algebraic concepts, and factoring is an essential skill for solving polynomial equations.
Example: x² + 3x + 2 (Polynomial), (x + 1)(x + 2) (Factoring)
2.4 Quadratic Equations and Functions
Quadratic equations are polynomial equations of degree two. These equations can be solved using various methods, including factoring, completing the square, and the quadratic formula. Quadratic functions are functions defined by quadratic equations, and their graphs are parabolas.
Example: x² – 4x + 3 = 0 (Quadratic Equation), f(x) = x² – 4x + 3 (Quadratic Function)
2.5 Exponential and Logarithmic Functions
Exponential functions involve a constant raised to a variable power, while logarithmic functions are the inverse of exponential functions. These functions are used to model growth, decay, and various other phenomena.
Example: f(x) = 2x (Exponential Function), g(x) = log2(x) (Logarithmic Function)
2.6 Radical Expressions and Equations
Radical expressions involve roots (such as square roots and cube roots) of numbers and variables. Solving radical equations involves isolating the radical and then raising both sides of the equation to the appropriate power.
Example: √x + 2 = 5 (Radical Equation), √x (Radical Expression)
2.7 Rational Expressions and Equations
Rational expressions are fractions in which the numerator and denominator are polynomials. Solving rational equations involves finding the values of the variables that make the equation true.
Example: (x + 1) / (x – 2) = 3 (Rational Equation), (x + 1) / (x – 2) (Rational Expression)
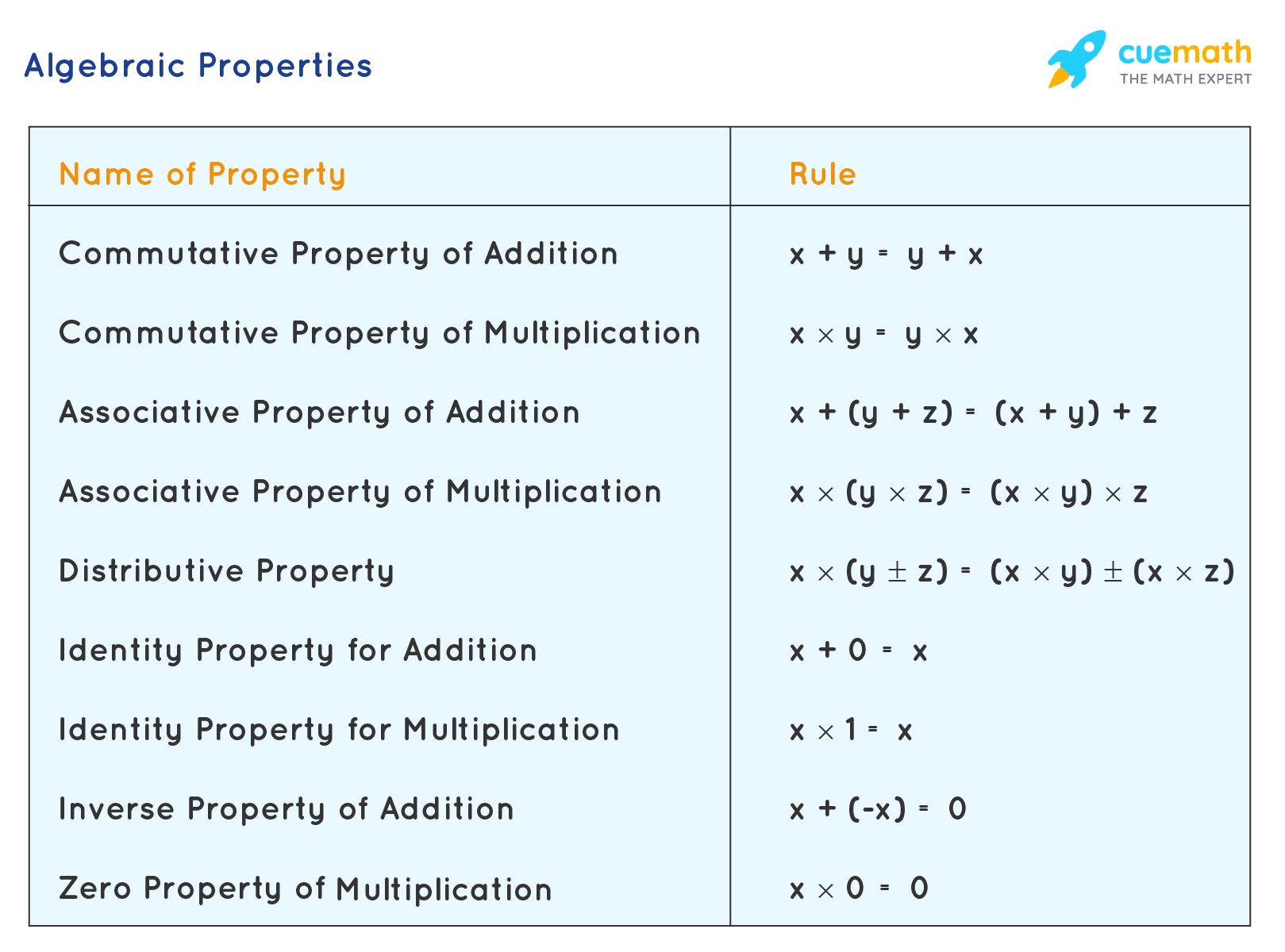
3. Essential Laws Governing Algebra
The laws of algebra provide the foundation for manipulating and simplifying algebraic expressions. Understanding these laws is crucial for solving equations and performing algebraic operations correctly. These laws ensure consistency and accuracy in algebraic manipulations.
3.1 Commutative Property
The commutative property states that the order of operations does not affect the result for addition and multiplication.
- Addition: a + b = b + a
- Multiplication: a b = b a
Example: 2 + 3 = 3 + 2, 4 5 = 5 4
3.2 Associative Property
The associative property states that the grouping of operations does not affect the result for addition and multiplication.
- Addition: (a + b) + c = a + (b + c)
- Multiplication: (a b) c = a (b c)
Example: (2 + 3) + 4 = 2 + (3 + 4), (4 5) 6 = 4 (5 6)
3.3 Distributive Property
The distributive property states that multiplying a number by a sum or difference is the same as multiplying the number by each term in the sum or difference.
- a (b + c) = a b + a * c
- a (b – c) = a b – a * c
Example: 2 (3 + 4) = 2 3 + 2 4, 3 (5 – 2) = 3 5 – 3 2
3.4 Identity Property
The identity property states that adding zero to a number or multiplying a number by one does not change the number.
- Addition: a + 0 = a
- Multiplication: a * 1 = a
Example: 5 + 0 = 5, 7 * 1 = 7
3.5 Inverse Property
The inverse property states that for every number, there exists an additive inverse (opposite) and a multiplicative inverse (reciprocal).
- Addition: a + (-a) = 0
- Multiplication: a * (1/a) = 1 (where a ≠ 0)
Example: 3 + (-3) = 0, 4 * (1/4) = 1
4. Fundamental Formulas in Algebra
Formulas are essential tools in algebra, providing a concise way to express mathematical relationships and solve problems. Memorizing and understanding these formulas is crucial for success in algebra.
4.1 Quadratic Formula
The quadratic formula is used to find the solutions (roots) of a quadratic equation in the form ax² + bx + c = 0.
- x = (-b ± √(b² – 4ac)) / (2a)
4.2 Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
4.3 Distance Formula
The distance formula is used to find the distance between two points (x1, y1) and (x2, y2) in a coordinate plane.
- d = √((x2 – x1)² + (y2 – y1)²)
4.4 Midpoint Formula
The midpoint formula is used to find the midpoint of a line segment with endpoints (x1, y1) and (x2, y2).
- Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
4.5 Pythagorean Theorem
The Pythagorean theorem relates the sides of a right triangle: a² + b² = c², where a and b are the lengths of the legs, and c is the length of the hypotenuse.
5. Algebra 1 vs. Algebra 2: Key Differences
Algebra 1 and Algebra 2 build upon each other, but they cover different topics and levels of complexity. Understanding the differences between these two courses is essential for planning your math education.
| Feature | Algebra 1 | Algebra 2 |
|---|---|---|
| Focus | Basic algebraic concepts and equation solving | Advanced algebraic concepts, functions, and their applications |
| Topics Covered | Linear equations, inequalities, polynomials, factoring | Exponential and logarithmic functions, complex numbers, conic sections, matrices |
| Equation Types | Linear and quadratic equations | Polynomial, rational, exponential, and logarithmic equations |
| Complexity | Introductory level | Advanced level |
| Prerequisites | Basic arithmetic | Algebra 1 |
| Real-World Applications | Introduction to problem-solving applications | Modeling complex scenarios, scientific applications, engineering applications |

5.1 Depth of Coverage
Algebra 1 focuses on building a solid foundation in algebraic principles. Algebra 2 delves deeper into these concepts and introduces new, more complex topics.
5.2 Mathematical Maturity
Algebra 2 requires a higher level of mathematical maturity and abstract thinking compared to Algebra 1. Students are expected to apply their knowledge to solve more challenging and multi-step problems.
6. Strategies and Tips for Mastering Algebra
Mastering algebra requires consistent effort, effective study habits, and a willingness to seek help when needed. Here are some strategies and tips to help you succeed in algebra.
6.1 Build a Strong Foundation
Ensure you have a solid understanding of basic arithmetic concepts before diving into algebra. Review fractions, decimals, percentages, and basic operations.
6.2 Practice Regularly
Practice is key to mastering algebra. Work through a variety of problems, and don’t be afraid to make mistakes. Mistakes are learning opportunities.
6.3 Seek Help When Needed
Don’t hesitate to ask for help from teachers, tutors, or classmates if you’re struggling with a concept. Seeking help early can prevent frustration and build confidence.
6.4 Use Visual Aids
Visual aids, such as graphs, diagrams, and charts, can help you understand algebraic concepts more clearly. Use these tools to visualize problems and solutions.
6.5 Break Down Complex Problems
Break down complex problems into smaller, more manageable steps. This can make the problem less intimidating and easier to solve.
6.6 Understand the “Why” Not Just the “How”
Focus on understanding the underlying principles and concepts, not just memorizing formulas and procedures. Knowing why a formula works can help you apply it in different situations.
7. Real-World Applications of Algebra
Algebra is not just an abstract mathematical concept; it has numerous real-world applications in various fields. Understanding these applications can make algebra more engaging and relevant.
7.1 Engineering
Engineers use algebra to design and analyze structures, circuits, and systems. Algebraic equations are used to model physical phenomena and solve engineering problems.
7.2 Computer Science
Computer scientists use algebra to develop algorithms, write code, and design computer systems. Algebraic concepts are fundamental to many areas of computer science, including cryptography, data structures, and artificial intelligence.
7.3 Economics
Economists use algebra to model economic systems, analyze data, and make predictions. Algebraic equations are used to represent supply and demand, calculate economic growth, and analyze financial markets.
7.4 Physics
Physicists use algebra to describe the physical world, model phenomena, and solve problems. Algebraic equations are used to represent motion, energy, forces, and other physical quantities.
7.5 Finance
Financial analysts use algebra to manage investments, analyze financial data, and make predictions about the market.
8. The Importance of Algebra in Higher Education
Algebra is a fundamental prerequisite for many higher education courses, particularly in STEM fields. A strong foundation in algebra can open doors to a wide range of academic and career opportunities.
8.1 Calculus
Calculus builds upon algebraic concepts, including functions, equations, and graphs. A solid understanding of algebra is essential for success in calculus.
8.2 Linear Algebra
Linear algebra is a branch of mathematics that deals with linear equations, vector spaces, and matrices. It is used in various fields, including computer graphics, data analysis, and engineering.
8.3 Differential Equations
Differential equations are equations that involve derivatives of functions. They are used to model various phenomena in physics, engineering, and biology.
8.4 Statistics
Statistics involves collecting, analyzing, and interpreting data. Algebraic concepts are used in statistical analysis to calculate probabilities, test hypotheses, and model data.
9. Common Challenges in Learning Algebra and How to Overcome Them
Learning algebra can be challenging, but with the right strategies and resources, you can overcome these challenges and succeed.
9.1 Abstract Concepts
Algebra involves abstract concepts that can be difficult to grasp. Use visual aids, real-world examples, and hands-on activities to make these concepts more concrete.
9.2 Formula Memorization
Memorizing formulas can be overwhelming. Focus on understanding the underlying principles and concepts, not just memorizing formulas.
9.3 Problem-Solving Skills
Developing problem-solving skills takes time and practice. Work through a variety of problems, and don’t be afraid to make mistakes.
9.4 Lack of Confidence
Lack of confidence can hinder your progress in algebra. Focus on your strengths, celebrate your successes, and seek help when needed.
9.5 Time Management
Effective time management is crucial for success in algebra. Set aside dedicated study time, and break down your tasks into smaller, more manageable steps.
10. Leveraging LEARNS.EDU.VN for Algebra Success
LEARNS.EDU.VN offers a comprehensive range of resources to help you succeed in algebra. From detailed explanations to practice problems, LEARNS.EDU.VN provides the tools and support you need to master algebra.
10.1 Detailed Explanations
LEARNS.EDU.VN provides detailed explanations of algebraic concepts, making it easier to understand and apply them.
10.2 Practice Problems
LEARNS.EDU.VN offers a wide range of practice problems to help you develop your problem-solving skills and build confidence.
10.3 Interactive Quizzes
LEARNS.EDU.VN provides interactive quizzes to test your knowledge and track your progress.
10.4 Expert Support
LEARNS.EDU.VN offers expert support from experienced educators who can answer your questions and provide guidance.
10.5 Customized Learning Paths
LEARNS.EDU.VN creates personalized learning paths tailored to your individual needs and learning style, ensuring you receive targeted instruction and support.
11. Advanced Algebraic Concepts and Their Applications
As you progress in algebra, you’ll encounter more advanced concepts that build upon the foundational knowledge you’ve acquired. These concepts are essential for further study in mathematics and related fields.
11.1 Matrices
Matrices are rectangular arrays of numbers that are used to solve systems of linear equations, perform transformations, and represent data.
11.2 Complex Numbers
Complex numbers are numbers that have a real part and an imaginary part. They are used in various fields, including electrical engineering, quantum mechanics, and fluid dynamics.
11.3 Conic Sections
Conic sections are curves that are formed by the intersection of a plane and a cone. They include circles, ellipses, parabolas, and hyperbolas.
11.4 Sequences and Series
Sequences are ordered lists of numbers, and series are the sums of the terms in a sequence. These concepts are used in calculus, statistics, and financial mathematics.
11.5 Mathematical Induction
Mathematical induction is a method of proving mathematical statements that involve natural numbers. It is used to establish the validity of formulas and theorems.
12. Algebra and Technology: Tools for Success
Technology plays a significant role in learning and applying algebra. Various tools and resources are available to help you visualize concepts, solve problems, and explore algebraic relationships.
12.1 Graphing Calculators
Graphing calculators are powerful tools for visualizing functions, solving equations, and analyzing data.
12.2 Computer Algebra Systems (CAS)
CAS software, such as Mathematica and Maple, can perform symbolic calculations, solve equations, and generate graphs.
12.3 Online Algebra Solvers
Online algebra solvers can help you check your work, solve problems, and learn from step-by-step solutions.
12.4 Educational Apps
Educational apps provide interactive lessons, practice problems, and quizzes to help you learn algebra on the go.
12.5 Virtual Manipulatives
Virtual manipulatives, such as algebra tiles and fraction bars, can help you visualize algebraic concepts and solve problems hands-on.
13. Algebra in Standardized Tests: What to Expect
Algebra is a significant component of many standardized tests, including the SAT, ACT, and GRE. Understanding the types of algebra questions that appear on these tests can help you prepare effectively.
13.1 SAT
The SAT includes algebra questions that test your ability to solve equations, manipulate expressions, and apply algebraic concepts to real-world problems.
13.2 ACT
The ACT includes algebra questions that cover a wide range of topics, including linear equations, quadratic equations, polynomials, and functions.
13.3 GRE
The GRE includes algebra questions that test your ability to solve equations, inequalities, and word problems.
13.4 Test-Taking Strategies
Developing effective test-taking strategies can help you maximize your score on standardized tests. These strategies include pacing yourself, eliminating incorrect answer choices, and reviewing your work.
13.5 Practice Tests
Taking practice tests is an essential part of preparing for standardized tests. Practice tests can help you identify your strengths and weaknesses and familiarize yourself with the test format.
14. Future Trends in Algebra Education
Algebra education is constantly evolving to meet the needs of students and the demands of the 21st century. Future trends in algebra education include:
14.1 Personalized Learning
Personalized learning involves tailoring instruction to meet the individual needs and learning styles of students.
14.2 Technology Integration
Technology integration involves using technology to enhance teaching and learning in algebra.
14.3 Real-World Applications
Emphasizing real-world applications can make algebra more engaging and relevant for students.
14.4 Collaborative Learning
Collaborative learning involves working with classmates to solve problems and learn from each other.
14.5 Project-Based Learning
Project-based learning involves engaging students in real-world projects that require them to apply algebraic concepts and skills.
15. Frequently Asked Questions About Algebra
Here are some frequently asked questions about algebra:
-
What is algebra used for in real life?
- Algebra is used in various fields, including engineering, computer science, economics, physics, and finance.
-
How can I improve my algebra skills?
- Practice regularly, seek help when needed, use visual aids, and break down complex problems.
-
What is the difference between an expression and an equation?
- An expression is a combination of variables, constants, and operations, while an equation is a statement that shows the equality between two expressions.
-
What is the quadratic formula used for?
- The quadratic formula is used to find the solutions (roots) of a quadratic equation in the form ax² + bx + c = 0.
-
What are the key topics covered in algebra?
- Key topics include linear equations, inequalities, polynomials, factoring, quadratic equations, functions, and radical expressions.
-
How does technology help in learning algebra?
- Technology provides tools for visualizing concepts, solving problems, and exploring algebraic relationships.
-
What is the importance of algebra in higher education?
- Algebra is a fundamental prerequisite for many higher education courses, particularly in STEM fields.
-
What is a system of linear equations?
- A system of linear equations involves two or more linear equations with the same variables.
-
What are polynomials?
- Polynomials are algebraic expressions that consist of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents.
-
What is the distributive property?
- The distributive property states that multiplying a number by a sum or difference is the same as multiplying the number by each term in the sum or difference.
Algebra is a powerful tool that can unlock your potential in mathematics and various other fields. By understanding the core principles, mastering the key topics, and leveraging the resources available at LEARNS.EDU.VN, you can achieve success in algebra and open doors to a world of opportunities. For more in-depth learning and personalized support, visit LEARNS.EDU.VN or contact us at 123 Education Way, Learnville, CA 90210, United States, Whatsapp: +1 555-555-1212. Let learns.edu.vn guide you on your journey to algebraic mastery and beyond! Explore algebraic thinking, mathematical expression, and equation solving today!
