Support Vector Machine (SVM) machine learning stands as a powerful and versatile tool in the realm of supervised learning, adept at tackling complex classification, regression, and outlier detection challenges. Join LEARNS.EDU.VN as we navigate the fundamentals of SVM, explore its multifaceted applications, and understand how it can be a game-changer in various industries. Discover the definition, workings, types, and real-world examples. Uncover machine learning algorithms, data science techniques, and predictive modeling strategies.
1. Defining Support Vector Machine (SVM) Machine Learning
A Support Vector Machine (SVM) is a supervised machine learning algorithm widely recognized for its effectiveness in addressing intricate classification, regression, and outlier detection problems. It functions by performing optimal data transformations that establish boundaries between data points, guided by predefined classes, labels, or outputs. This makes SVMs incredibly versatile across various fields, including healthcare, natural language processing, signal processing, and image and speech recognition.
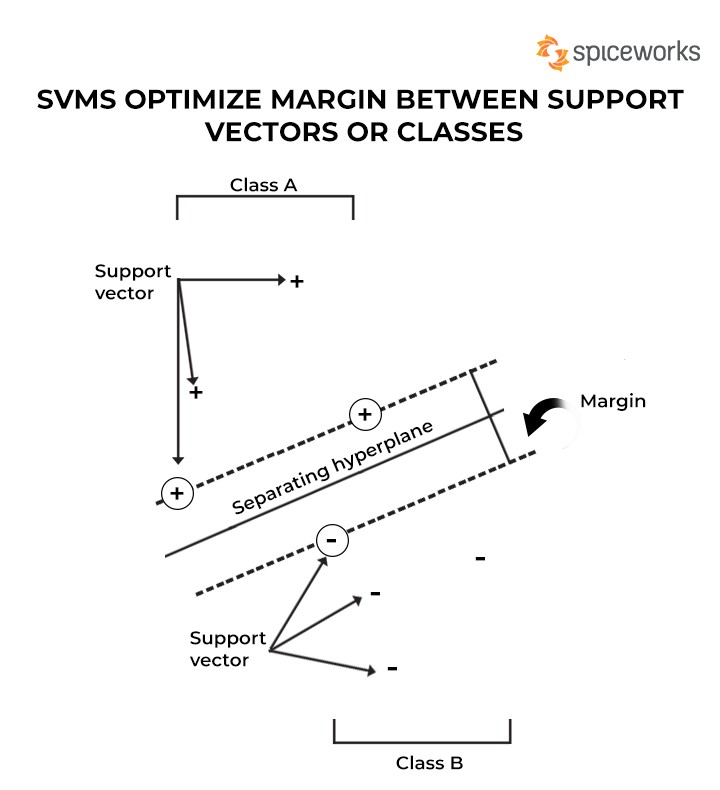SVMs Optimize Margin Between Support Vectors or Classes
1.1. Key Objective of SVM
The primary goal of an SVM algorithm is to pinpoint a hyperplane that distinctly segregates data points belonging to different classes. The hyperplane is strategically positioned to maximize the margin, which is the distance between the hyperplane and the nearest data points from each class. This margin maximization enhances the SVM’s ability to generalize well on unseen data.
1.2. Practical Challenges and Solutions
While SVMs are inherently designed for binary classification problems, their adaptability extends to multiclass problems. This is achieved by constructing and combining multiple binary classifiers, effectively transforming the multiclass problem into a series of binary classifications.
1.3. The Kernel Trick
At its core, an SVM employs kernel methods to transform data features using kernel functions. These functions map complex datasets into higher dimensions, facilitating easier data point separation. This technique, known as the “kernel trick,” efficiently transforms data without the computational burden of explicitly mapping it into higher dimensions.
1.4. Historical Context
The foundational concept of SVM was introduced in 1963 by Vladimir N. Vapnik and Alexey Ya. Chervonenkis. Since then, SVMs have garnered significant attention and have been applied in diverse areas such as protein sorting, text categorization, facial recognition, autonomous vehicles, and robotic systems.
2. Understanding How SVM Works: A Step-by-Step Approach
To grasp the workings of a Support Vector Machine, let’s consider an example with red and black labels, represented by features x and y. Our aim is to create a classifier that categorizes data points into either the red or black category.
2.1. Visualizing Data Points
First, we plot the labeled data on an x-y plane. The SVM then uses a hyperplane, which is a two-dimensional line in this case, to separate the red and black data points. This hyperplane acts as the decision boundary, determining which category each data point belongs to.
Alt Text: Data points scattered on an x-y plane, representing the features of two different classes.
2.2. Maximizing the Margin
The hyperplane is positioned to maximize the margin between the two closest labels (red and black). The larger the margin, the easier it is to classify the data.
2.3. Handling Non-Linear Data
The above scenario applies to linearly separable data. However, real-world data is often non-linear, making it impossible to separate data points with a straight line.
Consider this non-linear, complex dataset:
Alt Text: Example of a non-linear dataset with data points intermixed, requiring higher-dimensional separation.
In such cases, we need to add another dimension to the feature space. For linear data, two dimensions (x and y) suffice. For non-linear data, we add a z-dimension to better classify the data points. For instance, we can use the equation for a circle: z = x² + y².
2.4. Transforming to Higher Dimensions
With the third dimension, the slice of feature space along the z-direction looks like this:
Alt Text: Visualization of data points in a three-dimensional space, showing separation along the z-axis.
Now, with three dimensions, the hyperplane runs parallel to the x-direction at a specific value of z (e.g., z=1). The data points are then mapped back to two dimensions.
2.5. Boundary Creation
The resulting figure reveals the boundary for data points along features x, y, and z, forming a circle that separates the two labels.
2.6. Visualizing in 3D
Another way to visualize this is by imagining tennis balls of two different colors lying on a 2D plane. If we lift the surface upward, the tennis balls distribute in the air. At one point, the two differently colored balls may separate, allowing us to place a surface between the two segregated sets.
2.7. Kernelling
The act of “lifting” the 2D surface represents mapping data into higher dimensions, a process known as “kernelling.” Complex data points can be separated with the help of more dimensions. The data points are mapped into higher dimensions until a hyperplane is identified that clearly separates them.
Alt Text: A 3D visualization illustrating how data points are separated into different categories using SVM.
3. Exploring the Different Types of Support Vector Machines
Support Vector Machines are broadly categorized into two main types: Simple or Linear SVM and Kernel or Non-Linear SVM.
3.1. Simple or Linear SVM
A Linear SVM is used to classify linearly separable data. This means that if a dataset can be divided into categories or classes using a single straight line, it is considered a linear SVM. The classifier that classifies such data is called a linear SVM classifier.
3.1.1. Applications
Simple SVMs are typically used for classification and regression analysis problems.
3.2. Kernel or Non-Linear SVM
Non-linear data that cannot be segregated into distinct categories with a straight line is classified using a Kernel or Non-Linear SVM. The classifier is referred to as a non-linear classifier. Classification can be performed by adding features into higher dimensions rather than relying on 2D space. The newly added features fit a hyperplane that helps easily separate classes or categories.
3.2.1. Applications
Kernel SVMs are typically used to handle optimization problems that have multiple variables.
4. Real-World Examples of Support Vector Machines in Action
SVMs, which rely on supervised learning methods to classify unknown data into known categories, find applications in diverse fields. Here are some prominent real-world examples:
4.1. Addressing the Geo-Sounding Problem
The geo-sounding problem, a widespread use case for SVMs, involves tracking the planet’s layered structure. It entails solving inversion problems where observations are used to factor in the variables or parameters that produced them.
Linear function and support vector algorithmic models separate the electromagnetic data. Linear programming practices are employed while developing supervised models. As the problem size is small, the dimension size is tiny, which accounts for mapping the planet’s structure.
4.2. Assessing Seismic Liquefaction Potential
Soil liquefaction is a significant concern during earthquakes. SVMs play a key role in determining the occurrence and non-occurrence of liquefaction. SVMs handle two tests: SPT (Standard Penetration Test) and CPT (Cone Penetration Test), which use field data to adjudicate the seismic status.
SVMs are used to develop models that involve soil factors and liquefaction parameters to determine ground surface strength. SVMs achieve an accuracy of close to 96-97% for such applications.
4.3. Protein Remote Homology Detection
Protein remote homology is a field of computational biology where proteins are categorized into structural and functional parameters depending on the sequence of amino acids when sequence identification is seemingly difficult. SVMs play a key role, with kernel functions determining the commonalities between protein sequences.
4.4. Data Classification
While SVMs solve complex mathematical problems, smooth SVMs are preferred for data classification, using smoothing techniques to reduce data outliers and make patterns identifiable.
Smooth SVMs use algorithms such as the Newton-Armijo algorithm to handle larger datasets. They explore math properties such as strong convexity for more straightforward data classification, even with non-linear data.
4.5. Facial Detection & Expression Classification
SVMs classify facial structures versus non-facial ones. Training data uses two classes of face entity (+1) and non-face entity (-1) and n*n pixels to distinguish between face and non-face structures. Each pixel is analyzed, and features from each one are extracted that denote face and non-face characters. The process creates a square decision boundary around facial structures based on pixel intensity and classifies the resultant images.
SVMs are also used for facial expression classification, including expressions denoted as happy, sad, angry, surprised, and so on.
4.6. Surface Texture Classification
SVMs are used for the classification of images of surfaces. Images clicked of surfaces can be fed into SVMs to determine the texture of surfaces and classify them as smooth or gritty surfaces.
4.7. Text Categorization & Handwriting Recognition
Text categorization refers to classifying data into predefined categories, such as news articles containing politics, business, the stock market, or sports. Emails can be segregated into spam, non-spam, junk, and others.
Each article or document is assigned a score, which is then compared to a predefined threshold value. The article is classified into its respective category depending on the evaluated score.
For handwriting recognition, the dataset containing passages that different individuals write is supplied to SVMs. SVM classifiers are trained with sample data initially and are later used to classify handwriting based on score values. SVMs are also used to segregate writings by humans and computers.
4.8. Speech Recognition
In speech recognition, words from speeches are individually picked and separated. For each word, certain features and characteristics are extracted using techniques such as Mel Frequency Cepstral Coefficients (MFCC), Linear Prediction Coefficients (LPC), and Linear Prediction Cepstral Coefficients (LPCC).
These methods collect audio data, feed it to SVMs, and then train the models for speech recognition.
4.9. Stenography Detection
With SVMs, you can determine whether any digital image is tampered with, contaminated, or pure. Such examples are helpful when handling security-related matters for organizations or government agencies, as it is easier to encrypt and embed data as a watermark in high-resolution images.
Such images contain more pixels; hence, it can be challenging to spot hidden or watermarked messages. One solution is to separate each pixel and store data in different datasets that SVMs can later analyze.
4.10. Cancer Detection
Medical professionals, researchers, and scientists worldwide have been working hard to find a solution that can effectively detect cancer in its early stages. Several AI and ML tools are being deployed for the same. For example, in January 2020, Google developed an AI tool that helps in early breast cancer detection and reduces false positives and negatives.
In such examples, SVMs can be employed, wherein cancerous images can be supplied as input. SVM algorithms can analyze them, train the models, and eventually categorize the images that reveal malign or benign cancer features.
Alt Text: Illustration of SVM being used to analyze medical images for cancer detection.
5. The Benefits of Using Support Vector Machines
Support Vector Machines (SVMs) offer numerous advantages in the realm of machine learning, making them a preferred choice for a wide range of applications. Here’s a detailed look at the benefits:
| Benefit | Description |
|---|---|
| Effective in High Dimensions | SVMs excel in handling datasets with a large number of features, making them suitable for complex problems where the dimensionality is high. |
| Memory Efficient | SVMs use a subset of training points in the decision function (called support vectors), making them memory efficient. |
| Versatile | Different Kernel functions can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels. |
| Effective with Non-Linear Data | SVMs can efficiently handle non-linear data by using the kernel trick, which implicitly maps inputs into high-dimensional feature spaces. |
| Regularization Capabilities | SVMs incorporate regularization to prevent overfitting, enhancing the model’s ability to generalize well on unseen data. |
| Clear Margin of Separation | SVMs aim to maximize the margin between classes, leading to better generalization and more robust classification. |
| Global Minima | SVMs are based on convex optimization, guaranteeing that any local minimum found is also the global minimum, leading to stable and reliable solutions. |
| Robust to Outliers | SVMs are relatively robust to outliers because they focus on support vectors that define the decision boundary, rather than being influenced by all data points. |
| High Accuracy | SVMs often provide high accuracy, especially when used with appropriate kernels and tuned hyperparameters. |
| Well-Suited for Text & Image | SVMs are particularly well-suited for text categorization and image classification, as demonstrated by their performance in numerous real-world applications. |
| Feature Importance Insights | SVMs can offer insights into feature importance, helping to identify which features are most influential in the classification process. |
| Handles Unstructured Data | SVMs can handle unstructured data effectively, allowing them to be used in applications where the data is not neatly organized or pre-processed. |
| Model Interpretability | Although not as transparent as some other models, SVMs can provide insights into the decision-making process, particularly when using linear kernels. |
| Scalability | While training can be computationally intensive, especially for large datasets, various optimization techniques can be employed to improve the scalability of SVMs. |
| Adaptability | SVMs can be adapted to various types of data and problems, making them a versatile choice for both classification and regression tasks. |
| Advanced Kernel Choices | SVMs offer a wide range of advanced kernel choices, enabling them to model complex relationships within the data. |
| No Distribution Assumptions | Unlike some other machine learning algorithms, SVMs do not assume any particular distribution of the data, making them more flexible in various scenarios. |
| Good Generalization | SVMs tend to generalize well from training data to unseen data, reducing the risk of overfitting and ensuring reliable performance in real-world applications. |
| Boundary Optimization | SVMs optimize the decision boundary effectively, leading to more accurate and reliable predictions. |
| Mathematical Foundation | The solid mathematical foundation of SVMs ensures that the models are stable and well-behaved, providing confidence in their performance. |
6. Challenges and Limitations of SVM Machine Learning
While Support Vector Machines (SVMs) offer numerous advantages, it’s important to be aware of their limitations. Here are some challenges and drawbacks associated with using SVMs:
6.1. Computational Intensity
Training SVMs can be computationally intensive, especially for large datasets. The time complexity typically ranges from O(n^2) to O(n^3), where n is the number of training samples.
6.2. Memory Requirements
SVMs require significant memory, particularly when using kernel methods. The kernel matrix, which stores the pairwise kernel values between all training samples, can consume a large amount of memory.
6.3. Parameter Tuning
SVM performance is highly dependent on the choice of kernel function and hyperparameters (e.g., C, gamma). Tuning these parameters can be challenging and time-consuming, often requiring cross-validation and grid search.
6.4. Kernel Selection
Choosing the right kernel function is crucial for SVM performance. However, there is no one-size-fits-all kernel, and selecting the appropriate kernel often requires domain expertise and experimentation.
6.5. Not Suitable for Very Large Datasets
SVMs may not be suitable for very large datasets due to their high computational and memory requirements. Other algorithms, such as stochastic gradient descent-based methods, may be more appropriate in such cases.
6.6. Lack of Transparency
SVMs can be less transparent than some other machine learning algorithms, such as decision trees or linear regression. The decision boundary in SVMs is defined by support vectors, which may not be easily interpretable.
6.7. Sensitivity to Noisy Data
SVMs can be sensitive to noisy data, especially if the noise is present near the decision boundary. Outliers and mislabeled data points can significantly affect the model’s performance.
6.8. Probability Estimation
SVMs do not naturally provide probability estimates. Additional techniques, such as Platt scaling, are required to estimate the probability of class membership.
6.9. Imbalanced Datasets
SVMs can perform poorly on imbalanced datasets, where one class has significantly more samples than the other. Techniques such as cost-sensitive learning or resampling may be necessary to address this issue.
6.10. Difficult to Scale
SVMs can be difficult to scale to very large datasets. Techniques such as decomposition methods or approximation algorithms may be necessary to handle such cases.
6.11. High Variance with Small Datasets
With small datasets, SVMs can exhibit high variance, meaning that the model’s performance can vary significantly depending on the specific training data.
6.12. Overfitting
SVMs are prone to overfitting, especially when the number of features is high relative to the number of training samples. Regularization techniques, such as L1 or L2 regularization, are necessary to prevent overfitting.
6.13. Requires Feature Scaling
SVMs are sensitive to the scale of the input features. Feature scaling, such as standardization or normalization, is typically required to ensure that all features contribute equally to the model.
6.14. Can Be Time-Consuming to Train
Training an SVM can be a time-consuming process, especially for large datasets or complex models.
6.15. Less Effective with Unstructured Data
SVMs are less effective with unstructured data, such as raw text or images, unless combined with feature extraction techniques.
6.16. Assumes Data is Linearly Separable
SVMs assume that the data is linearly separable in some high-dimensional space. If this assumption is violated, the model may perform poorly.
6.17. Requires a Good Understanding of the Data
Effective use of SVMs requires a good understanding of the data, including its characteristics and potential limitations.
6.18. Difficult to Interpret for Non-Linear Kernels
Interpreting the decision boundary can be challenging when using non-linear kernels, as the mapping to high-dimensional space is implicit.
6.19. Assumes Data is Independently and Identically Distributed (IID)
SVMs assume that the data is independently and identically distributed (IID). If this assumption is violated, the model’s performance may be affected.
6.20. Can Be Difficult to Debug
Debugging an SVM model can be challenging, especially if the model is complex or the data is noisy.
7. SVM vs. Other Machine Learning Algorithms: A Comparative Analysis
When choosing a machine learning algorithm, it’s crucial to understand the strengths and weaknesses of each option and how they compare to others. Here’s a comparison of Support Vector Machines (SVMs) with other popular algorithms like Logistic Regression, Decision Trees, and Neural Networks:
7.1. SVM vs. Logistic Regression
| Feature | SVM | Logistic Regression |
|---|---|---|
| Type | Supervised learning, primarily for classification but also regression | Supervised learning for classification |
| Complexity | Can handle complex non-linear relationships with kernel trick | Linear model, can handle non-linear relationships with feature engineering |
| Interpretability | Less interpretable, especially with non-linear kernels | More interpretable, coefficients can be understood as log-odds ratios |
| Use Cases | Image classification, text categorization, bioinformatics | Binary classification problems, credit scoring, marketing analytics |
| Strengths | Effective in high dimensional spaces, memory efficient, versatile with different kernel functions | Simple, easy to implement, provides probability estimates, interpretable |
| Limitations | Computationally intensive for large datasets, sensitive to parameter tuning, kernel selection can be tricky | Assumes linear relationship between features and log-odds, may underperform with complex non-linear data |
7.2. SVM vs. Decision Trees
| Feature | SVM | Decision Trees |
|---|---|---|
| Type | Supervised learning, primarily for classification but also regression | Supervised learning for classification and regression |
| Complexity | Can handle complex non-linear relationships with kernel trick | Can handle non-linear relationships through splits in the feature space |
| Interpretability | Less interpretable, especially with non-linear kernels | Highly interpretable, easy to visualize and understand the decision-making process |
| Use Cases | Image classification, text categorization, bioinformatics | Credit risk assessment, medical diagnosis, customer segmentation |
| Strengths | Effective in high dimensional spaces, memory efficient, versatile with different kernel functions | Simple, easy to implement, handles both categorical and numerical data, non-parametric (no assumptions about data distribution) |
| Limitations | Computationally intensive for large datasets, sensitive to parameter tuning, kernel selection can be tricky | Prone to overfitting, can be unstable (small changes in data can lead to different trees), biased towards features with more levels |
7.3. SVM vs. Neural Networks
| Feature | SVM | Neural Networks |
|---|---|---|
| Type | Supervised learning, primarily for classification but also regression | Supervised learning for classification and regression |
| Complexity | Can handle complex non-linear relationships with kernel trick | Can model highly complex non-linear relationships with multiple layers |
| Interpretability | Less interpretable, especially with non-linear kernels | Black box model, difficult to interpret the decision-making process |
| Use Cases | Image classification, text categorization, bioinformatics | Image recognition, natural language processing, speech recognition |
| Strengths | Effective in high dimensional spaces, memory efficient, versatile with different kernel functions, less prone to overfitting compared to simpler neural networks | Can learn highly complex patterns, feature learning (automatically extracts relevant features), state-of-the-art performance in many tasks |
| Limitations | Computationally intensive for large datasets, sensitive to parameter tuning, kernel selection can be tricky | Computationally expensive, requires large amounts of data, prone to overfitting, requires careful hyperparameter tuning, black box model |
7.4. Summary of When to Use Each Algorithm
- SVM: Use when you have high-dimensional data, a clear margin of separation between classes, and when interpretability is not a primary concern.
- Logistic Regression: Use for binary classification problems when interpretability is important and the relationship between features and the target variable is approximately linear.
- Decision Trees: Use when you need an interpretable model, can handle both categorical and numerical data, and when you want a non-parametric approach.
- Neural Networks: Use when you have large amounts of data, need to model highly complex non-linear relationships, and when you prioritize performance over interpretability.
8. Advanced Techniques and Extensions in SVM
Support Vector Machines (SVMs) have evolved significantly since their inception, with various advanced techniques and extensions developed to enhance their performance and applicability. Here’s an overview of some of these advanced concepts:
8.1. Kernel Engineering
- Custom Kernels: Developing custom kernels tailored to specific datasets can significantly improve SVM performance. These kernels can incorporate domain knowledge and capture complex relationships within the data.
- Kernel Combination: Combining multiple kernels can leverage the strengths of different kernel functions, leading to more robust and accurate models. Techniques like Multiple Kernel Learning (MKL) automate the process of finding optimal kernel combinations.
8.2. Optimization Techniques
- Sequential Minimal Optimization (SMO): SMO is a popular algorithm for training SVMs, particularly for large datasets. It breaks the optimization problem into a series of smaller subproblems, making it more computationally efficient.
- Stochastic Gradient Descent (SGD): SGD can be used to train linear SVMs more efficiently, especially for very large datasets. Techniques like mini-batch SGD can further improve performance.
- Decomposition Methods: Decomposition methods divide the optimization problem into smaller, more manageable subproblems, allowing for parallel processing and improved scalability.
8.3. Regularization Techniques
- L1 Regularization: L1 regularization adds a penalty term to the objective function, encouraging sparsity in the model by driving some feature weights to zero. This can lead to more interpretable models and improved generalization.
- L2 Regularization: L2 regularization adds a penalty term to the objective function, discouraging large feature weights. This can help prevent overfitting and improve the model’s stability.
- Elastic Net Regularization: Elastic Net regularization combines L1 and L2 regularization, providing a balance between sparsity and stability.
8.4. Handling Imbalanced Datasets
- Cost-Sensitive Learning: Cost-sensitive learning assigns different costs to misclassifying samples from different classes, allowing the model to prioritize the minority class.
- Resampling Techniques: Resampling techniques, such as oversampling the minority class or undersampling the majority class, can balance the class distribution and improve SVM performance.
- One-Class SVM: One-Class SVM is used for anomaly detection, where the goal is to identify samples that deviate significantly from the majority class.
8.5. Multi-Class SVM
- One-vs-All (OVA): OVA trains a separate SVM for each class, treating the samples from that class as positive and all other samples as negative.
- One-vs-One (OVO): OVO trains a separate SVM for each pair of classes, resulting in a larger number of SVMs but potentially better performance.
- Error-Correcting Output Codes (ECOC): ECOC encodes each class as a binary code, allowing for error correction during classification.
8.6. Transductive SVM
- Transductive SVM (TSVM): TSVM uses unlabeled data to improve the model’s performance by finding the optimal decision boundary that separates the labeled and unlabeled samples.
8.7. Online SVM
- Online SVM: Online SVMs can update the model incrementally as new data becomes available, making them suitable for dynamic environments.
8.8. Fuzzy SVM
- Fuzzy SVM: Fuzzy SVM assigns fuzzy membership values to each sample, allowing for more flexible decision boundaries and improved robustness to noisy data.
8.9. Deep Learning and SVM Hybrid Models
- Combining Deep Learning Features with SVM: Using features extracted from deep learning models as input to SVMs can leverage the strengths of both approaches, leading to state-of-the-art performance in various tasks.
8.10. Applications in Specific Domains
- Bioinformatics: SVMs are widely used in bioinformatics for tasks such as protein classification, gene expression analysis, and drug discovery.
- Computer Vision: SVMs are used in computer vision for tasks such as image classification, object detection, and facial recognition.
- Natural Language Processing: SVMs are used in natural language processing for tasks such as text categorization, sentiment analysis, and spam detection.
9. Best Practices for Implementing SVM Machine Learning
Implementing Support Vector Machines (SVMs) effectively requires careful planning and execution. Here are some best practices to ensure optimal performance and reliable results:
9.1. Data Preprocessing
- Clean and Prepare Data: Ensure your data is clean, accurate, and properly formatted. Handle missing values, outliers, and inconsistencies appropriately.
- Feature Scaling: Scale your features to a similar range using techniques like standardization (Z-score) or Min-Max scaling. SVMs are sensitive to the scale of input features.
- Feature Selection: Select relevant features and remove irrelevant or redundant ones. This can improve model performance and reduce computational complexity.
9.2. Kernel Selection
- Experiment with Different Kernels: Try different kernel functions (e.g., linear, polynomial, RBF) and evaluate their performance using cross-validation.
- Understand Kernel Properties: Understand the properties of each kernel and choose one that is appropriate for your data. For example, the RBF kernel is suitable for non-linear data, while the linear kernel is suitable for linearly separable data.
- Consider Custom Kernels: If you have domain knowledge about your data, consider developing a custom kernel function that captures the specific relationships within the data.
9.3. Hyperparameter Tuning
- Use Cross-Validation: Use cross-validation to tune the hyperparameters of your SVM model. This will help you find the optimal hyperparameter values that generalize well to unseen data.
- Grid Search or Random Search: Use grid search or random search to explore the hyperparameter space. Grid search exhaustively searches all possible hyperparameter combinations, while random search randomly samples hyperparameter values.
- Understand Hyperparameter Effects: Understand the effects of each hyperparameter on model performance. For example, the C parameter controls the trade-off between maximizing the margin and minimizing the classification error.
9.4. Model Evaluation
- Use Appropriate Evaluation Metrics: Use appropriate evaluation metrics to assess the performance of your SVM model. Common metrics include accuracy, precision, recall, F1-score, and AUC-ROC.
- Consider Class Imbalance: If your data is imbalanced, consider using metrics that are robust to class imbalance, such as precision-recall curve or F1-score.
- Use Holdout Set: Use a holdout set to evaluate the final performance of your model. This will give you an unbiased estimate of how well your model generalizes to unseen data.
9.5. Interpretability
- Understand Support Vectors: Understand the role of support vectors in defining the decision boundary. Support vectors are the data points that lie closest to the decision boundary and have the greatest influence on the model.
- Visualize Decision Boundary: Visualize the decision boundary to gain insights into how your model is making predictions.
- Feature Importance: If you are using a linear kernel, you can extract feature importance scores to understand which features are most influential in the classification process.
9.6. Regularization
- Use Regularization Techniques: Use regularization techniques (e.g., L1 or L2 regularization) to prevent overfitting. Regularization adds a penalty term to the objective function, discouraging large feature weights and improving the model’s ability to generalize well to unseen data.
9.7. Computational Efficiency
- Use Efficient Algorithms: Use efficient algorithms for training SVM models, such as Sequential Minimal Optimization (SMO) or Stochastic Gradient Descent (SGD).
- Consider Decomposition Methods: If you have a large dataset, consider using decomposition methods to divide the optimization problem into smaller, more manageable subproblems.
- Parallel Processing: Use parallel processing to speed up the training process.
9.8. Monitoring and Maintenance
- Monitor Model Performance: Monitor the performance of your SVM model over time and retrain it as needed.
- Handle Concept Drift: If your data distribution changes over time, you may need to update your model to handle concept drift.
- Document Your Process: Document your entire process, including data preprocessing steps, kernel selection, hyperparameter tuning, model evaluation, and monitoring procedures.
10. Frequently Asked Questions (FAQs) About SVM Machine Learning
10.1. What is the primary goal of the SVM algorithm?
The primary goal of the SVM algorithm is to find a hyperplane that distinctly separates data points of different classes while maximizing the margin between the hyperplane and the nearest data points.
10.2. How does the “kernel trick” work in SVM?
The “kernel trick” is a technique used to transform data features by employing kernel functions. It maps complex datasets into higher dimensions, facilitating easier data point separation without the computational burden of explicitly mapping the data.
10.3. What are the two main types of Support Vector Machines?
The two main types of Support Vector Machines are:
- Simple or Linear SVM: Used for classifying linearly separable data.
- Kernel or Non-Linear SVM: Used for classifying non-linear data by adding features into higher dimensions.
10.4. Can SVMs be used for both classification and regression tasks?
Yes, SVMs can be used for both classification and regression tasks, although they are primarily known for their effectiveness in classification problems.
10.5. What is the role of support vectors in SVM?
Support vectors are the data points that lie closest to the decision boundary and have the greatest influence on the model. They define the decision boundary and play a critical role in SVM.
10.6. How does feature scaling affect SVM performance?
SVMs are sensitive to the scale of the input features. Feature scaling, such as standardization or normalization, is typically required to ensure that all features contribute equally to the model and improve performance.
10.7. What is the C parameter in SVM and how does it affect model performance?
The C parameter in SVM controls the trade-off between maximizing the margin and minimizing the classification error. A smaller value of C encourages a larger margin, while a larger value of C allows for a smaller margin and fewer classification errors.
10.8. How do you handle imbalanced datasets in SVM?
To handle imbalanced datasets in SVM, techniques such as cost-sensitive learning (assigning different costs to misclassifying samples from different classes) or resampling techniques (oversampling the minority class or undersampling the majority class) can be used.
10.9. Are SVMs suitable for very large datasets?
SVMs may not be suitable for very large datasets due to their high computational and memory requirements. However, techniques such as stochastic gradient descent-based methods or decomposition methods can be used to handle larger datasets more efficiently.
10.10. Can SVMs provide probability estimates for class membership?
SVMs do not naturally provide probability estimates. Additional techniques, such as Platt scaling, are required to estimate the probability of class membership.
Conclusion: Embracing the Power of SVM with LEARNS.EDU.VN
SVMs stand out as a crucial tool in developing applications that involve predictive models. They are user-friendly and offer a sophisticated machine-learning algorithm to process linear and non-linear data through kernels. SVMs find applications across various domains and real-life scenarios where data is handled by adding higher-dimensional spaces.
Ready to dive deeper into the world of machine learning? At LEARNS.EDU.VN, we offer a wealth of resources to help you master SVM and other cutting-edge technologies. Explore our comprehensive articles, detailed guides, and hands-on courses designed to elevate your skills and knowledge.
- Explore Articles and Guides: Visit LEARNS.EDU.VN for in-depth content on SVM, machine learning, and data science.
- Discover Courses: Check out our diverse range of courses designed to transform you into a machine learning expert.
Address: 123 Education Way, Learnville, CA 90210, United States
Whatsapp: +1 555-555-1212
Website: LEARNS.EDU.VN
Unlock your potential with LEARNS.EDU.VN and become a leader in the ever-evolving world of artificial intelligence! Discover more at learns.edu.vn today.
