What Math Do 7th Graders Learn: A Comprehensive Guide

What Math Do 7th Graders Learn? Seventh grade math is a crucial year for building a strong mathematical foundation, and LEARNS.EDU.VN is here to guide you through it. Understanding the core concepts, from number systems to geometry, sets the stage for success in higher-level math courses and real-world applications. Explore effective learning strategies and resources at learns.edu.vn to master these vital skills, focusing on topics like algebraic thinking, geometric reasoning, and proportional relationships.

1. Mastering the Number System in 7th Grade Math

In 7th grade, students solidify their understanding of the number system, which is fundamental for all future mathematical endeavors. This involves working extensively with rational numbers, including decimals, fractions, and percentages. Students delve into the operations of addition, subtraction, multiplication, and division involving both positive and negative numbers. A key element is the ability to interpret and compute with these numbers in various forms and contexts, setting the foundation for more advanced algebraic concepts.

1.1. Understanding Rational Numbers

Rational numbers are any numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. This includes integers, fractions, terminating decimals, and repeating decimals. Mastering rational numbers involves understanding their properties and how to perform operations with them.

• Integers: These are whole numbers and their negatives (e.g., -3, -2, -1, 0, 1, 2, 3).
• Fractions: These represent parts of a whole (e.g., 1/2, 3/4, 5/8).
• Decimals: These are numbers written in base-10 notation, which can be terminating (e.g., 0.25) or repeating (e.g., 0.333…).

1.2. Operations with Positive and Negative Numbers

Seventh graders learn to perform all four basic arithmetic operations (addition, subtraction, multiplication, and division) with positive and negative numbers. This requires understanding the rules for signs:

• Addition:
  • Adding two positive numbers results in a positive number.
  • Adding two negative numbers results in a negative number.
  • Adding a positive and a negative number requires finding the difference between their absolute values and using the sign of the number with the larger absolute value.
• Subtraction: Subtracting a number is the same as adding its opposite.
• Multiplication:
  • Multiplying two numbers with the same sign (both positive or both negative) results in a positive number.
  • Multiplying two numbers with different signs results in a negative number.
• Division: The rules for signs in division are the same as in multiplication.

1.3. Absolute Value

Absolute value is the distance of a number from zero on the number line. It is always non-negative. The absolute value of a number x is denoted as |x|. For example:

• |5| = 5
• |-5| = 5

Understanding absolute value is crucial for solving equations and inequalities, as well as for interpreting real-world situations involving distance or magnitude.

1.4. Real-World Applications

Applying these number system concepts to real-world scenarios helps students see the relevance and practicality of math. Examples include:

• Temperature: Understanding how to calculate temperature changes, especially with negative temperatures.
• Finance: Managing bank accounts, debts, and credits.
• Measurement: Calculating distances, areas, and volumes.

Example Problem:

• A submarine is at -250 feet relative to sea level. It descends an additional 150 feet. What is the submarine’s new depth?

Solution:

• New depth = -250 + (-150) = -400 feet

This type of problem reinforces the understanding of adding negative numbers in a real-world context.

Concept	Explanation	Example
Rational Numbers	Numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero.	1/2, -3/4, 0.75, -0.333…
Positive and Negative Numbers	Numbers greater than zero (positive) and numbers less than zero (negative).	Positive: 5, 10, 2.5; Negative: -3, -7, -1.5
Absolute Value	The distance of a number from zero on the number line, always non-negative.
Real-World Applications	Applying number system concepts to practical situations.	Calculating temperature changes, managing finances, measuring distances.

Alt: Number line illustrating the position of rational numbers including fractions and decimals.

2. Expressions and Equations: Building Algebraic Thinking

Seventh grade math places a significant emphasis on expressions and equations. Students transition from basic arithmetic to algebraic thinking, using variables to represent unknown quantities and solving multi-step equations and inequalities. This prepares them for more advanced algebra in subsequent grades.

2.1. Variables and Algebraic Expressions

A variable is a symbol (usually a letter) that represents an unknown number. An algebraic expression is a combination of variables, numbers, and operations. For example:

• 3x + 5
• 2y – 7z

Seventh graders learn to simplify algebraic expressions by combining like terms and using the distributive property.

Combining Like Terms:

• Like terms are terms that have the same variable raised to the same power. For example, 3x and 5x are like terms, but 3x and 5x² are not.

• To combine like terms, add or subtract their coefficients.

  • Example: 3x + 5x = 8x

Distributive Property:

• The distributive property states that a(b + c) = ab + ac.

• This property is used to remove parentheses in algebraic expressions.

  • Example: 2(x + 3) = 2x + 6

2.2. Solving Multi-Step Equations

Solving equations involves finding the value of the variable that makes the equation true. Seventh graders learn to solve multi-step equations using inverse operations. The goal is to isolate the variable on one side of the equation.

Steps to Solve Multi-Step Equations:

1. Simplify both sides of the equation by combining like terms and using the distributive property.
2. Add or subtract to isolate the variable term on one side of the equation.
3. Multiply or divide to solve for the variable.

Example:

• Solve for x: 3x + 5 = 20

  1. Subtract 5 from both sides: 3x = 15
  2. Divide both sides by 3: x = 5

2.3. Inequalities and Their Graphs

An inequality is a statement that compares two expressions using inequality symbols such as >, <, ≥, or ≤. Solving inequalities involves finding the range of values for the variable that makes the inequality true.

Inequality Symbols:

• > means “greater than”
• < means “less than”
• ≥ means “greater than or equal to”
• ≤ means “less than or equal to”

Graphing Inequalities:

• Inequalities can be graphed on a number line.
• Use an open circle (o) for > and <, indicating that the endpoint is not included in the solution.
• Use a closed circle (•) for ≥ and ≤, indicating that the endpoint is included in the solution.

Example:

• Solve and graph the inequality: 2x – 3 < 7

  1. Add 3 to both sides: 2x < 10
  2. Divide both sides by 2: x < 5
  3. Graph: Draw a number line with an open circle at 5 and shade to the left.

2.4. Real-World Problem Solving

Applying expressions and equations to real-world problems helps students develop critical thinking and problem-solving skills. Examples include:

• Word Problems: Translating word problems into algebraic equations and solving them.
• Financial Planning: Calculating costs, profits, and budgets.
• Measurement Problems: Solving for unknown dimensions in geometric figures.

Example Problem:

• A store sells shirts for $15 each and has a fixed cost of $200 per day. How many shirts must the store sell to make a profit of at least $500?

Solution:

• Let n be the number of shirts sold.

• Profit = 15n – 200

• We want the profit to be at least $500, so: 15n – 200 ≥ 500

  1. Add 200 to both sides: 15n ≥ 700
  2. Divide both sides by 15: n ≥ 46.67

• Since the store can’t sell a fraction of a shirt, they must sell at least 47 shirts to make a profit of at least $500.

Concept	Explanation	Example
Variables	Symbols (usually letters) that represent unknown numbers.	x, y, z
Algebraic Expressions	Combinations of variables, numbers, and operations.	3x + 5, 2y – 7z
Multi-Step Equations	Equations that require multiple steps to solve.	2x + 3 = 7
Inequalities	Statements that compare two expressions using inequality symbols.	x > 3, y ≤ 5
Real-World Problems	Applying algebraic concepts to practical situations.	Calculating profits, solving measurement problems.

Alt: Step-by-step example of solving a multi-step algebraic equation.

3. Geometry: Exploring Shapes and Their Properties

Geometry is a significant component of 7th grade math, focusing on the properties of two-dimensional (2-D) and three-dimensional (3-D) shapes. Students learn to calculate area, volume, and surface area, as well as understand geometric relationships and vocabulary.

3.1. Area and Circumference of a Circle

A circle is a fundamental geometric shape defined as the set of all points equidistant from a central point. Key terms associated with circles include:

• Radius (r): The distance from the center of the circle to any point on the circle.
• Diameter (d): The distance across the circle through the center. Note that d = 2r.
• Circumference (C): The distance around the circle.
• Area (A): The amount of space enclosed by the circle.

Formulas:

• Circumference: C = 2πr = πd
• Area: A = πr²

where π (pi) is a mathematical constant approximately equal to 3.14159.

Example:

• Find the area and circumference of a circle with a radius of 5 cm.

  • Area: A = π*(5 cm)² = 25π cm² ≈ 78.54 cm²
  • Circumference: C = 2π*(5 cm) = 10π cm ≈ 31.42 cm

3.2. Surface Area of 2-D and 3-D Objects

Surface area is the total area of the surfaces of a three-dimensional object. Seventh graders learn to calculate the surface area of various shapes, including:

• Rectangular Prism: The sum of the areas of all six rectangular faces.
• Cube: 6 times the area of one square face.
• Cylinder: The sum of the areas of the two circular bases and the lateral surface.
• Pyramid: The sum of the area of the base and the areas of the triangular faces.

Formulas:

• Rectangular Prism: SA = 2(lw + lh + wh) where l is length, w is width, and h is height.
• Cube: SA = 6s² where s is the side length.
• Cylinder: SA = 2πr² + 2πrh where r is the radius and h is the height.

Example:

• Find the surface area of a rectangular prism with length 4 cm, width 3 cm, and height 2 cm.

  • SA = 2((4 cm)(3 cm) + (4 cm)(2 cm) + (3 cm)(2 cm))
  • SA = 2(12 cm² + 8 cm² + 6 cm²)
  • SA = 2(26 cm²) = 52 cm²

3.3. Volume of 3-D Objects

Volume is the amount of space inside a three-dimensional object. Seventh graders learn to calculate the volume of various shapes, including:

• Rectangular Prism: The product of length, width, and height.
• Cube: The side length cubed.
• Cylinder: The area of the base times the height.
• Cone: One-third the area of the base times the height.
• Sphere: Four-thirds pi times the radius cubed.

Formulas:

• Rectangular Prism: V = lwh where l is length, w is width, and h is height.
• Cube: V = s³ where s is the side length.
• Cylinder: V = πr²h where r is the radius and h is the height.
• Cone: V = (1/3)πr²h where r is the radius and h is the height.
• Sphere: V = (4/3)πr³ where r is the radius.

Example:

• Find the volume of a cylinder with a radius of 3 cm and a height of 7 cm.

  • V = π(3 cm)²(7 cm)
  • V = π(9 cm²)(7 cm)
  • V = 63π cm³ ≈ 197.92 cm³

3.4. Geometric Vocabulary

Understanding and using correct geometric vocabulary is crucial for describing shapes and their properties accurately. Key terms include:

• Polygon: A closed, two-dimensional shape formed by straight line segments.
• Triangle: A polygon with three sides.
• Quadrilateral: A polygon with four sides.
• Pentagon: A polygon with five sides.
• Hexagon: A polygon with six sides.
• Angle: The measure of the space between two intersecting lines or surfaces.
• Supplementary Angles: Two angles that add up to 180 degrees.
• Complementary Angles: Two angles that add up to 90 degrees.
• Parallel Lines: Lines that never intersect.
• Perpendicular Lines: Lines that intersect at a 90-degree angle.

Activity:

• Create vocabulary cards with definitions and diagrams to help remember geometric terms.

Concept	Explanation	Example
Area	The amount of space enclosed by a two-dimensional shape.	Area of a circle: A = πr²
Circumference	The distance around a circle.	Circumference of a circle: C = 2πr
Surface Area	The total area of the surfaces of a three-dimensional object.	Surface area of a rectangular prism: SA = 2(lw + lh + wh)
Volume	The amount of space inside a three-dimensional object.	Volume of a cylinder: V = πr²h
Geometric Terms	Vocabulary used to describe shapes and their properties, such as polygons, angles, parallel lines, and perpendicular lines.	Supplementary angles, complementary angles, parallel lines, perpendicular lines

Alt: Various geometric shapes including triangles, squares, circles, and prisms with labeled dimensions.

4. Functions: An Introduction to Mathematical Relationships (8th Grade Preview)

While functions are formally introduced in 8th grade, 7th graders may get a preview of this concept. A function is a rule that assigns to each input exactly one output. Understanding functions is critical for advanced math topics like algebra and calculus.

4.1. Understanding the Concept of a Function

A function can be thought of as a machine that takes an input, performs a specific operation, and produces an output. The input is often referred to as the independent variable (x), and the output is the dependent variable (y), because its value depends on the input.

Key Concepts:

• Input (Domain): The set of all possible values that can be entered into the function.
• Output (Range): The set of all possible values that the function can produce.
• Function Rule: The operation or set of operations that the function performs on the input to produce the output.

4.2. Representing Functions

Functions can be represented in several ways:

• Equation: A mathematical equation that defines the relationship between the input and output.

  • Example: y = 2x + 3

• Table: A table that lists pairs of input and output values.

  x (Input)	y (Output)
  1	5
  2	7
  3	9

• Graph: A visual representation of the function on a coordinate plane. The input (x) is plotted on the horizontal axis, and the output (y) is plotted on the vertical axis.

• Verbal Description: A description of the function in words.

  • Example: “The output is equal to twice the input plus three.”

4.3. Identifying Functions

To determine if a relationship is a function, check if each input has exactly one output. This can be done using the vertical line test on a graph: if any vertical line intersects the graph more than once, the relationship is not a function.

Example:

• Consider the equation y = x². This is a function because for every value of x, there is only one value of y.
• Consider the equation x = y². This is not a function because for some values of x, there are two values of y. For example, if x = 4, then y can be 2 or -2.

4.4. Real-World Examples

Functions can be used to model real-world relationships. Examples include:

• Cost Function: The relationship between the number of items purchased and the total cost.
• Distance Function: The relationship between the time traveled and the distance covered.
• Temperature Function: The relationship between the time of day and the temperature.

Example Problem:

• A taxi charges $3 for the first mile and $2 for each additional mile. Write a function to represent the total cost of a taxi ride.

Solution:

• Let x be the number of miles traveled.
• Let y be the total cost of the taxi ride.
• Function: y = 3 + 2(x – 1) for x ≥ 1

Concept	Explanation	Example
Function	A rule that assigns to each input exactly one output.	y = 2x + 3
Input (Domain)	The set of all possible values that can be entered into the function.	In y = 2x + 3, the input is x.
Output (Range)	The set of all possible values that the function can produce.	In y = 2x + 3, the output is y.
Representation	Functions can be represented as equations, tables, graphs, or verbal descriptions.	Equation: y = x²; Table: Input/Output values; Graph: Plotted on a coordinate plane.
Real-World Use	Functions can be used to model real-world relationships, such as cost, distance, and temperature.	Cost function, distance function, temperature function

Alt: Graph of a linear function showing the relationship between input and output values.

5. Proportional Relationships and Ratios

Understanding proportional relationships and ratios is a critical component of 7th grade math. These concepts form the foundation for understanding scaling, percentages, and more advanced topics like linear equations and similarity in geometry.

5.1. Understanding Ratios

A ratio is a comparison of two quantities. It can be expressed in several ways:

• Fraction: a/b
• Colon: a : b
• Words: “a to b”

Example:

• If there are 12 apples and 15 oranges in a fruit basket, the ratio of apples to oranges is 12/15, which simplifies to 4/5 or 4:5.

5.2. Proportions

A proportion is an equation stating that two ratios are equal. It can be written as:

• a/b = c/d

where a, b, c, and d are numbers, and b and d are not zero.

Solving Proportions:

• To solve a proportion, cross-multiply and then solve for the unknown variable.

  • Example: Solve for x in the proportion 3/4 = x/20

    1. Cross-multiply: 3 20 = 4 x
    2. Simplify: 60 = 4x
    3. Divide by 4: x = 15

5.3. Proportional Relationships

Two quantities are said to be in a proportional relationship if their ratios are constant. This means that as one quantity increases, the other quantity increases by a constant factor.

Identifying Proportional Relationships:

• Check if the ratio between the two quantities is constant.
• Graph the relationship on a coordinate plane. If the graph is a straight line passing through the origin (0,0), the relationship is proportional.

Example:

• The cost of buying apples is proportional to the number of apples purchased. If 5 apples cost $2, then 10 apples will cost $4, and 15 apples will cost $6. The ratio of cost to number of apples is always 2/5.

5.4. Scale Drawings and Scale Factors

Scale drawings are used to represent objects or areas that are too large or too small to be drawn at their actual size. A scale factor is the ratio of the length in the drawing to the corresponding length in the actual object.

Using Scale Factors:

• To find the actual length, multiply the length in the drawing by the scale factor.
• To find the length in the drawing, divide the actual length by the scale factor.

Example:

• A map has a scale of 1 inch = 50 miles. If the distance between two cities on the map is 3.5 inches, what is the actual distance between the cities?

  • Actual distance = 3.5 inches * 50 miles/inch = 175 miles

5.5. Percentages

A percentage is a ratio that compares a number to 100. It is a way of expressing a fraction or a decimal as a part of 100.

Converting Between Fractions, Decimals, and Percentages:

• Fraction to Decimal: Divide the numerator by the denominator.
• Decimal to Percentage: Multiply the decimal by 100 and add the percent sign (%).
• Percentage to Decimal: Divide the percentage by 100.
• Decimal to Fraction: Write the decimal as a fraction with a denominator of 10, 100, 1000, etc., and simplify.

Example:

• Convert 3/4 to a percentage.

  1. Divide 3 by 4: 3 ÷ 4 = 0.75
  2. Multiply by 100: 0.75 * 100 = 75%

Finding the Percentage of a Number:

• To find the percentage of a number, convert the percentage to a decimal and multiply it by the number.

  • Example: What is 20% of 80?

    1. Convert 20% to a decimal: 20% ÷ 100 = 0.20
    2. Multiply by 80: 0.20 * 80 = 16

Concept	Explanation	Example
Ratio	A comparison of two quantities.	3:5 (3 to 5)
Proportion	An equation stating that two ratios are equal.	2/3 = 4/6
Proportional Relationship	A relationship where the ratio between two quantities is constant.	Cost of items based on quantity: If 1 item costs $2, then 2 items cost $4, 3 items cost $6.
Scale Factor	The ratio of the length in a drawing to the corresponding length in the actual object.	1 inch = 10 miles on a map
Percentage	A ratio that compares a number to 100.	75% (75 out of 100)

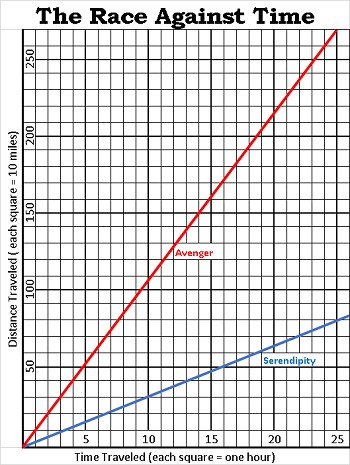Proportional Relationship Graph

Alt: Graph of a proportional relationship showing a straight line passing through the origin.

6. Statistics and Probability: Making Sense of Data

Seventh grade math introduces basic concepts in statistics and probability, equipping students with the tools to collect, organize, analyze, and interpret data, as well as to understand the likelihood of events.

6.1. Collecting and Organizing Data

Data collection is the process of gathering information. Data can be collected through surveys, experiments, observations, and other methods. Once collected, data needs to be organized in a meaningful way. Common methods include:

• Frequency Tables: A table that shows the number of times each value or category appears in a data set.
• Bar Graphs: A graph that uses bars to represent the frequency of each category.
• Histograms: A graph that displays the distribution of numerical data by dividing it into intervals and showing the frequency of each interval.
• Pie Charts: A circular chart that shows the proportion of each category as a percentage of the whole.

Example:

• A survey of 30 students about their favorite color yielded the following results:

  • Red: 8
  • Blue: 10
  • Green: 7
  • Yellow: 5

• This data can be organized in a frequency table and represented in a bar graph or pie chart.

6.2. Analyzing Data: Measures of Central Tendency

Measures of central tendency are used to describe the typical or average value in a data set. The three main measures are:

• Mean: The sum of all values divided by the number of values.
• Median: The middle value when the data is arranged in order.
• Mode: The value that appears most frequently in the data set.

Example:

• Consider the following data set: 5, 8, 8, 10, 12

  • Mean: (5 + 8 + 8 + 10 + 12) / 5 = 43 / 5 = 8.6
  • Median: 8 (the middle value)
  • Mode: 8 (appears twice)

6.3. Measures of Variability

Measures of variability describe the spread or dispersion of the data. Common measures include:

• Range: The difference between the largest and smallest values.
• Interquartile Range (IQR): The difference between the third quartile (Q3) and the first quartile (Q1). The quartiles divide the data set into four equal parts.
• Mean Absolute Deviation (MAD): The average of the absolute differences between each value and the mean.

Example:

• Consider the following data set: 5, 8, 8, 10, 12

  • Range: 12 – 5 = 7

  • To find the IQR:

    1. Arrange the data in order: 5, 8, 8, 10, 12
    2. Find the median (Q2): 8
    3. Find Q1 (median of the lower half): 5, 8 -> Q1 = 6.5
    4. Find Q3 (median of the upper half): 10, 12 -> Q3 = 11
    5. IQR = Q3 – Q1 = 11 – 6.5 = 4.5

  • To find the MAD:

    1. Calculate the mean: 8.6
    2. Find the absolute differences from the mean: |5-8.6|=3.6, |8-8.6|=0.6, |8-8.6|=0.6, |10-8.6|=1.4, |12-8.6|=3.4
    3. Calculate the average of the absolute differences: (3.6 + 0.6 + 0.6 + 1.4 + 3.4) / 5 = 9.6 / 5 = 1.92
    4. MAD = 1.92

6.4. Understanding Probability

Probability is the measure of how likely an event is to occur. It is expressed as a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain.

Basic Probability:

• The probability of an event is calculated as:

  • P(event) = (Number of favorable outcomes) / (Total number of possible outcomes)

Example:

• What is the probability of rolling a 4 on a fair six-sided die?

  • Number of favorable outcomes: 1 (rolling a 4)
  • Total number of possible outcomes: 6 (1, 2, 3, 4, 5, 6)
  • P(rolling a 4) = 1/6

6.5. Experimental vs. Theoretical Probability

• Theoretical Probability: What you expect to happen based on the nature of the event (e.g., the probability of flipping heads on a fair coin is 1/2).
• Experimental Probability: What actually happens when you conduct an experiment (e.g., flipping a coin 100 times and observing 55 heads).

Example:

• A coin is flipped 50 times, and it lands on heads 28 times.

  • Theoretical probability of heads: 1/2 = 0.5
  • Experimental probability of heads: 28/50 = 0.56

Concept	Explanation	Example
Data Collection	The process of gathering information through surveys, experiments, or observations.	Surveying students about their favorite subject.
Measures of Central Tendency	Values that describe the typical or average value in a data set, including mean, median, and mode.	Mean: (2 + 4 + 6) / 3 = 4; Median: 5 (in the set 1, 3, 5, 7, 9); Mode: 7 (in the set 2, 4, 7, 7, 9)
Measures of Variability	Values that describe the spread or dispersion of the data, including range, interquartile range (IQR), and mean absolute deviation (MAD).	Range: 10 – 2 = 8 (in the set 2, 4, 6, 8, 10); IQR: Q3 – Q1; MAD: Average of the absolute differences between each value and the mean.
Probability	The measure of how likely an event is to occur, expressed as a number between 0 and 1.	The probability of rolling a 3 on a six-sided die: 1/6
Theoretical vs. Experimental Probability	Theoretical probability is what you expect to happen, while experimental probability is what actually happens when you conduct an experiment.	Theoretical probability of flipping heads: 1/2; Experimental probability: Flipping a coin 50 times and observing 20 heads: 20/50 = 0.4

*Alt: Examples