When Do You Learn Pythagorean Theorem: A Comprehensive Guide

When Do You Learn Pythagorean Theorem? The Pythagorean theorem, a fundamental concept in geometry, unlocks a world of problem-solving possibilities. At LEARNS.EDU.VN, we guide you through understanding its application and significance. Master this theorem, explore real-world scenarios, and enhance your math skills with our expert resources and tailored learning paths, including insights into geometrical concepts, mathematical problem-solving, and educational resources, making it easier than ever.

1. Introduction to the Pythagorean Theorem

The Pythagorean theorem is a cornerstone of geometry, linking the sides of a right-angled triangle in a precise and elegant relationship. Understanding when and how you learn this theorem is crucial for building a strong foundation in mathematics and its various applications. This section provides a comprehensive overview of the theorem, its historical context, and its relevance in modern education.

1.1. What is the Pythagorean Theorem?

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides (the legs, or cathetus). This relationship is expressed by the equation:

$a^2 + b^2 = c^2$

Where:

a and b are the lengths of the two shorter sides (legs) of the right triangle.
c is the length of the hypotenuse.

This theorem is fundamental not only in mathematics but also in various fields such as physics, engineering, and computer science. Its simplicity and wide applicability make it an essential tool for problem-solving and analytical thinking.

1.2. Historical Context

The theorem is named after the ancient Greek mathematician Pythagoras, who is credited with providing a formal proof. However, the relationship between the sides of a right-angled triangle was known to earlier civilizations, including the Babylonians and Egyptians. These cultures used this knowledge for practical purposes such as land surveying and construction.

Babylonians: The Babylonian tablet YBC 7289 (c. 1800 BC) contains a diagram that implies knowledge of the Pythagorean theorem.
Egyptians: Egyptian surveyors likely used a rope with knots at equal intervals to form right angles, a practical application of the 3-4-5 triangle (a Pythagorean triple).
Pythagoras (c. 570 – c. 495 BC): Pythagoras and his followers are credited with the first formal proof of the theorem, establishing its mathematical validity.

The formalization of the theorem by Pythagoras marked a significant milestone in the development of mathematical theory, transitioning from empirical observation to deductive reasoning.

1.3. Relevance in Modern Education

The Pythagorean theorem is typically introduced in middle school or early high school mathematics curricula. It serves as a bridge between arithmetic and more advanced topics in algebra and geometry.

Middle School (Grades 7-8): Students are introduced to the theorem through hands-on activities, visual proofs, and simple problem-solving exercises.
High School (Grades 9-10): The theorem is revisited with more rigorous proofs and applications in coordinate geometry, trigonometry, and calculus.
Higher Education: The Pythagorean theorem is a foundational concept in many STEM fields, including engineering, physics, and computer science.

LEARNS.EDU.VN provides comprehensive resources for students at all levels, ensuring a solid understanding of the Pythagorean theorem and its applications. Our materials include detailed explanations, interactive exercises, and real-world examples to enhance learning and retention.

2. Curriculum Integration: When the Theorem is Taught

The Pythagorean theorem’s introduction and reinforcement are strategically placed within the mathematics curriculum to build upon prior knowledge and prepare students for future studies. This section outlines the typical grade levels, subjects, and learning objectives associated with teaching the Pythagorean theorem.

2.1. Grade Levels and Timing

The Pythagorean theorem is generally introduced in middle school, specifically around the 7th or 8th grade, depending on the curriculum structure. Here’s a typical timeline:

7th Grade: Introduction to the concept, often through visual demonstrations and simple applications.
8th Grade: Formal teaching of the theorem, including proofs and problem-solving exercises.
9th-10th Grade (High School): Reinforcement and extension of the theorem in geometry and algebra courses.

The timing allows students to grasp the basics of algebra and geometry before delving into the Pythagorean theorem. This sequencing ensures that students have the necessary skills to understand and apply the theorem effectively.

2.2. Relevant Subjects

The Pythagorean theorem is primarily taught in the context of the following subjects:

Geometry: The theorem is a fundamental part of geometry, used to solve problems involving right triangles, areas, and volumes.
Algebra: Algebraic skills are essential for manipulating the equation $a^2 + b^2 = c^2$ and solving for unknown variables.
Trigonometry: The theorem provides a basis for understanding trigonometric ratios and functions in right triangles.
Pre-Calculus/Calculus: In higher-level math courses, the theorem is used in more complex problems involving vectors, complex numbers, and three-dimensional geometry.

LEARNS.EDU.VN integrates the Pythagorean theorem into various subjects, providing a holistic learning experience. Our resources include cross-curricular activities that demonstrate the theorem’s relevance in different contexts.

2.3. Learning Objectives

The key learning objectives when teaching the Pythagorean theorem include:

Understanding the Theorem: Students should be able to state and explain the Pythagorean theorem.
Identifying Right Triangles: Students should be able to identify right triangles and their components (legs and hypotenuse).
Applying the Theorem: Students should be able to use the theorem to find the length of an unknown side in a right triangle.
Solving Problems: Students should be able to apply the theorem to solve real-world problems involving distances, areas, and volumes.
Proving the Theorem: Students should be able to understand and reproduce basic proofs of the Pythagorean theorem.

To achieve these objectives, LEARNS.EDU.VN offers interactive modules, practice problems, and step-by-step solutions. Our resources are designed to cater to different learning styles, ensuring that all students can master the Pythagorean theorem.

3. Prerequisites: Building Blocks for Understanding

Before diving into the Pythagorean theorem, students need a solid foundation in several fundamental mathematical concepts. These prerequisites ensure that students can grasp the theorem’s logic and apply it effectively. This section outlines the essential building blocks that pave the way for understanding the Pythagorean theorem.

3.1. Basic Algebra Skills

Algebraic proficiency is crucial for working with the Pythagorean theorem. Key skills include:

Solving Equations: Students must be able to solve linear and quadratic equations. For example, solving for c in the equation $a^2 + b^2 = c^2$ requires understanding how to isolate variables and take square roots.
Working with Exponents: Understanding exponents and how to square numbers is fundamental to applying the theorem. Students should be familiar with the concept of squaring a number (e.g., $5^2 = 25$).
Simplifying Expressions: Students should be able to simplify algebraic expressions involving square roots and exponents.

LEARNS.EDU.VN provides comprehensive algebra resources that cover these essential skills. Our interactive exercises and step-by-step solutions help students build confidence and competence in algebra.

3.2. Geometry Fundamentals

A basic understanding of geometry is essential for grasping the concepts behind the Pythagorean theorem. Key areas include:

Understanding Triangles: Students should be able to identify different types of triangles, including right triangles, acute triangles, and obtuse triangles.
Angle Measurement: Knowledge of angle measurement, particularly the concept of a right angle (90 degrees), is crucial for identifying right triangles.
Area and Perimeter: Understanding how to calculate the area and perimeter of basic shapes provides a context for applying the Pythagorean theorem in more complex problems.

Our geometry modules at LEARNS.EDU.VN offer detailed explanations and visual aids to help students master these fundamental concepts.

3.3. Number Sense and Operations

Strong number sense and operational skills are vital for accurate calculations when applying the Pythagorean theorem. Key skills include:

Arithmetic Operations: Students should be proficient in addition, subtraction, multiplication, and division.
Fractions and Decimals: Understanding how to work with fractions and decimals is essential for solving problems involving non-integer side lengths.
Square Roots: Students need to understand square roots and how to estimate them, as finding the length of a side often involves taking the square root of a sum.

LEARNS.EDU.VN offers a variety of resources to enhance number sense and operational skills, including practice quizzes and real-world problem scenarios.

3.4. Proportional Reasoning

Proportional reasoning is crucial for understanding the relationships between the sides of similar triangles, which often involves the Pythagorean theorem.

Ratios and Proportions: Students should be able to set up and solve proportions, understanding how ratios relate the sides of similar triangles.
Scale Factors: An understanding of scale factors helps in problems where triangles are scaled up or down, while maintaining their proportions.

LEARNS.EDU.VN includes interactive lessons and exercises to develop proportional reasoning skills, preparing students for more advanced geometric concepts.

4. Methods for Teaching the Pythagorean Theorem

Effective teaching methods are crucial for helping students understand and apply the Pythagorean theorem. This section explores various strategies that educators can use to make the theorem accessible and engaging.

4.1. Visual and Hands-On Approaches

Visual and hands-on activities can significantly enhance students’ understanding of the Pythagorean theorem. Some effective strategies include:

Geometric Demonstrations: Using physical models or diagrams to demonstrate the relationship between the squares of the sides of a right triangle. For example, cutting out squares from paper and arranging them to show that the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the legs.
Interactive Software: Utilizing interactive software or online tools that allow students to manipulate right triangles and observe how changing the side lengths affects the relationship between the sides.
Real-World Examples: Presenting real-world examples, such as using the theorem to calculate the distance across a diagonal field or the height of a ladder leaning against a wall.

LEARNS.EDU.VN offers a range of visual and interactive resources, including virtual labs and animated demonstrations, to support hands-on learning.

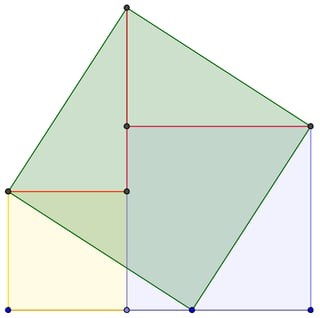
4.2. Proofs of the Theorem

Presenting different proofs of the Pythagorean theorem can help students appreciate its mathematical validity and develop their logical reasoning skills. Some common proofs include:

Algebraic Proof: Using algebraic manipulation to show that $a^2 + b^2 = c^2$ based on the properties of similar triangles.
Geometric Proof: Demonstrating the theorem by comparing areas of squares and triangles, often involving visual dissection and rearrangement.
Euclid’s Proof: Following the classic proof from Euclid’s Elements, which uses geometric constructions to show the relationship between the areas of the squares.

LEARNS.EDU.VN provides detailed explanations of these proofs, along with interactive diagrams to help students visualize the steps involved.

4.3. Problem-Solving Strategies

Teaching effective problem-solving strategies is essential for helping students apply the Pythagorean theorem in different contexts. Key strategies include:

Understanding the Problem: Emphasizing the importance of reading the problem carefully and identifying what is being asked.
Drawing Diagrams: Encouraging students to draw diagrams to visualize the problem and label the known and unknown quantities.
Applying the Theorem: Guiding students on how to correctly apply the Pythagorean theorem to find the unknown side length.
Checking the Answer: Teaching students to check their answer to ensure it makes sense in the context of the problem.

LEARNS.EDU.VN offers a wide variety of practice problems, ranging from simple to complex, with step-by-step solutions to guide students through the problem-solving process.

4.4. Incorporating Technology

Technology can play a significant role in enhancing the teaching of the Pythagorean theorem. Some effective ways to incorporate technology include:

Online Simulations: Using online simulations that allow students to explore the theorem by manipulating the sides of a right triangle and observing the effects.
Interactive Whiteboards: Utilizing interactive whiteboards to draw diagrams, solve problems, and engage students in collaborative activities.
Educational Apps: Incorporating educational apps that provide practice problems, quizzes, and interactive lessons on the Pythagorean theorem.

LEARNS.EDU.VN integrates technology seamlessly into its learning resources, offering interactive simulations, virtual labs, and adaptive assessments to enhance the learning experience.

5. Real-World Applications of the Pythagorean Theorem

The Pythagorean theorem is not just an abstract mathematical concept; it has numerous practical applications in various fields. This section explores some real-world scenarios where the theorem is used.

5.1. Construction and Architecture

In construction and architecture, the Pythagorean theorem is used to ensure that buildings are square and that structures are stable.

Building Foundations: Builders use the 3-4-5 rule (a Pythagorean triple) to ensure that the corners of a building foundation are right angles.
Roofing: The theorem is used to calculate the length of rafters needed for a roof, given the height and span of the roof.
Staircase Design: Architects use the theorem to determine the proper rise and run of stairs, ensuring that they are safe and comfortable to use.

LEARNS.EDU.VN provides case studies and examples of how the Pythagorean theorem is applied in construction and architecture, helping students see the practical relevance of the theorem.

5.2. Navigation and Surveying

The Pythagorean theorem is essential in navigation and surveying for determining distances and positions.

GPS Systems: GPS systems use the theorem to calculate the distance between satellites and receivers, allowing for accurate positioning.
Land Surveying: Surveyors use the theorem to measure distances and angles, creating accurate maps and property boundaries.
Air and Sea Navigation: Navigators use the theorem to calculate distances and bearings, helping them to navigate ships and airplanes.

LEARNS.EDU.VN offers interactive simulations that demonstrate how the Pythagorean theorem is used in navigation and surveying, enhancing students’ understanding of these applications.

5.3. Engineering and Design

Engineers and designers use the Pythagorean theorem in various applications, from designing bridges to creating computer graphics.

Bridge Design: Engineers use the theorem to calculate the lengths of suspension cables and support structures in bridges.
Mechanical Engineering: The theorem is used to calculate the forces and stresses in mechanical systems, ensuring that they are safe and efficient.
Computer Graphics: Computer graphics designers use the theorem to calculate distances and positions in three-dimensional space, creating realistic images and animations.

LEARNS.EDU.VN provides detailed examples of how the Pythagorean theorem is applied in engineering and design, showcasing its importance in these fields.

5.4. Everyday Applications

The Pythagorean theorem also has many everyday applications that people may not even realize.

Finding the Shortest Route: Calculating the shortest distance across a rectangular park or field.
Hanging a Picture: Ensuring that a picture is hung straight by measuring the diagonals.
Determining TV Size: Understanding how the size of a TV is measured diagonally.

LEARNS.EDU.VN includes engaging examples of everyday applications of the Pythagorean theorem, making the theorem more relatable and relevant to students’ lives.

6. Common Challenges and Misconceptions

Despite its fundamental nature, students often face challenges and develop misconceptions when learning the Pythagorean theorem. This section addresses some common issues and provides strategies for overcoming them.

6.1. Difficulty Identifying the Hypotenuse

One common challenge is difficulty identifying the hypotenuse in a right triangle. Students may confuse the hypotenuse with one of the legs, leading to incorrect application of the theorem.

Strategy: Emphasize that the hypotenuse is always opposite the right angle and is the longest side of the triangle. Use visual aids and hands-on activities to reinforce this concept.

LEARNS.EDU.VN offers interactive exercises that help students practice identifying the hypotenuse in different orientations of right triangles.

6.2. Incorrectly Applying the Formula

Another common mistake is applying the Pythagorean theorem incorrectly, such as adding the squares of the hypotenuse and one leg to find the other leg.

Strategy: Clearly explain the formula $a^2 + b^2 = c^2$ and emphasize that c represents the hypotenuse. Provide plenty of practice problems that require students to solve for different variables.

LEARNS.EDU.VN provides step-by-step solutions to practice problems, helping students understand the correct application of the formula.

6.3. Confusion with Non-Right Triangles

Students may mistakenly apply the Pythagorean theorem to triangles that are not right triangles.

Strategy: Emphasize that the Pythagorean theorem only applies to right triangles. Teach students how to identify right triangles and explain why the theorem does not work for other types of triangles.

LEARNS.EDU.VN includes lessons that cover different types of triangles and their properties, helping students distinguish right triangles from others.

6.4. Difficulty with Square Roots

Many students struggle with calculating square roots, which is necessary for finding the length of a side when applying the Pythagorean theorem.

Strategy: Review the concept of square roots and provide practice in estimating and calculating them. Use calculators or online tools to assist with calculations, but also encourage students to understand the underlying concept.

LEARNS.EDU.VN offers resources on square roots, including practice quizzes and tutorials, to help students build confidence in this area.

6.5. Lack of Real-World Context

Students may struggle to see the relevance of the Pythagorean theorem if it is presented only as an abstract mathematical concept.

Strategy: Provide real-world examples and applications of the theorem, such as those discussed in Section 5. This will help students understand why the theorem is important and how it is used in everyday life.

LEARNS.EDU.VN incorporates real-world examples into its lessons and practice problems, making the theorem more engaging and relevant for students.

7. Advanced Topics and Extensions

Once students have a solid understanding of the basic Pythagorean theorem, they can explore more advanced topics and extensions. This section introduces some of these areas.

7.1. Pythagorean Triples

Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem (e.g., 3-4-5, 5-12-13). Exploring these triples can deepen students’ understanding of the theorem and its properties.

Generating Triples: Teach students how to generate Pythagorean triples using formulas such as $a = m^2 – n^2$, $b = 2mn$, and $c = m^2 + n^2$, where m and n are positive integers with $m > n$.
Properties of Triples: Discuss the properties of Pythagorean triples, such as the fact that they can be primitive (where a, b, and c have no common factors) or non-primitive (where they do).

LEARNS.EDU.VN offers resources on Pythagorean triples, including examples, exercises, and interactive tools for generating triples.

7.2. Distance Formula

The distance formula, which is used to calculate the distance between two points in a coordinate plane, is a direct application of the Pythagorean theorem.

Derivation: Show students how the distance formula is derived from the Pythagorean theorem by considering the horizontal and vertical distances between two points as the legs of a right triangle.
Applications: Provide practice problems that involve using the distance formula to find the distance between points, the length of a line segment, or the perimeter of a polygon.

LEARNS.EDU.VN includes lessons on the distance formula, with examples and practice problems that demonstrate its connection to the Pythagorean theorem.

7.3. Trigonometry

The Pythagorean theorem is a fundamental concept in trigonometry, as it forms the basis for defining trigonometric ratios in right triangles.

Trigonometric Ratios: Introduce students to the trigonometric ratios (sine, cosine, tangent) and explain how they relate the sides of a right triangle to its angles.
Applications: Provide practice problems that involve using trigonometric ratios to solve for unknown side lengths or angles in right triangles.

LEARNS.EDU.VN offers a comprehensive introduction to trigonometry, with lessons on trigonometric ratios, applications, and interactive simulations.

7.4. Three-Dimensional Geometry

The Pythagorean theorem can be extended to three-dimensional geometry to solve problems involving distances and angles in three-dimensional space.

3D Distance Formula: Introduce the three-dimensional distance formula, which is an extension of the two-dimensional formula based on the Pythagorean theorem.
Applications: Provide problems that involve finding the distance between points in three-dimensional space, the length of a diagonal in a rectangular prism, or the angle between a line and a plane.

LEARNS.EDU.VN includes resources on three-dimensional geometry, with examples and practice problems that demonstrate the application of the Pythagorean theorem in this context.

8. Tips for Parents and Educators

Parents and educators play a crucial role in helping students understand and appreciate the Pythagorean theorem. This section offers tips for supporting students’ learning.

8.1. Creating a Supportive Learning Environment

Encourage Questions: Create an environment where students feel comfortable asking questions and seeking help when they are struggling.
Provide Feedback: Offer constructive feedback on students’ work, focusing on both their strengths and areas for improvement.
Celebrate Success: Acknowledge and celebrate students’ achievements, no matter how small, to build their confidence and motivation.

LEARNS.EDU.VN provides resources for parents and educators, including tips for creating a supportive learning environment and strategies for motivating students.

8.2. Utilizing Online Resources

Explore LEARNS.EDU.VN: Take advantage of the comprehensive resources available at LEARNS.EDU.VN, including lessons, practice problems, interactive simulations, and real-world examples.
Use Educational Apps: Incorporate educational apps that provide practice problems, quizzes, and interactive lessons on the Pythagorean theorem.
Watch Video Tutorials: Utilize video tutorials that explain the Pythagorean theorem and its applications in a clear and engaging manner.

LEARNS.EDU.VN offers a wide range of online resources to support students’ learning, including interactive lessons, practice problems, and video tutorials.

8.3. Connecting Math to Real Life

Point Out Applications: Help students see the relevance of the Pythagorean theorem by pointing out its applications in everyday life, such as in construction, navigation, and design.
Engage in Activities: Engage in activities that involve using the Pythagorean theorem, such as measuring the diagonal of a room or calculating the height of a tree.
Visit Relevant Sites: Visit construction sites, museums, or other places where the Pythagorean theorem is used, to provide students with real-world context.

LEARNS.EDU.VN incorporates real-world examples into its lessons and practice problems, making the theorem more engaging and relevant for students.

8.4. Encouraging Practice and Review

Regular Practice: Encourage students to practice regularly to reinforce their understanding of the Pythagorean theorem.
Review Concepts: Review key concepts periodically to ensure that students retain their knowledge and can apply it effectively.
Use Flashcards: Utilize flashcards to help students memorize the Pythagorean theorem and its applications.

LEARNS.EDU.VN provides a variety of practice problems, quizzes, and flashcards to help students review and reinforce their understanding of the Pythagorean theorem.

9. Latest Trends in Teaching the Pythagorean Theorem

The field of education is constantly evolving, and new trends are emerging in how the Pythagorean theorem is taught. This section explores some of these trends.

9.1. Personalized Learning

Personalized learning involves tailoring instruction to meet the individual needs and learning styles of each student. This approach can be particularly effective in teaching the Pythagorean theorem.

Adaptive Assessments: Use adaptive assessments to identify students’ strengths and weaknesses, and then provide targeted instruction to address their specific needs.
Flexible Pacing: Allow students to progress at their own pace, providing additional support for those who are struggling and challenging those who are ready to move on.
Choice-Based Activities: Offer students a choice of activities and assignments, allowing them to engage with the material in a way that is most meaningful to them.

LEARNS.EDU.VN supports personalized learning by offering adaptive assessments, flexible pacing options, and a variety of activities and assignments to cater to different learning styles.

9.2. Gamification

Gamification involves incorporating game-like elements into the learning experience to make it more engaging and motivating. This approach can be used to teach the Pythagorean theorem in a fun and interactive way.

Online Games: Use online games that require students to apply the Pythagorean theorem to solve problems and earn points or rewards.
Classroom Competitions: Organize classroom competitions or challenges that involve using the Pythagorean theorem to solve real-world problems.
Badges and Leaderboards: Award badges or points for completing activities and create leaderboards to recognize and reward students’ achievements.

LEARNS.EDU.VN incorporates gamification elements into its learning resources, offering online games, classroom competitions, and badges to motivate students and enhance their learning experience.

9.3. Project-Based Learning

Project-based learning involves engaging students in real-world projects that require them to apply their knowledge and skills to solve authentic problems. This approach can be used to teach the Pythagorean theorem in a meaningful and relevant way.

Design a Building: Challenge students to design a building or structure that incorporates the Pythagorean theorem in its design.
Plan a Trip: Have students plan a trip that involves calculating distances and using the Pythagorean theorem to determine the shortest route.
Create a Game: Task students with creating a game that requires players to use the Pythagorean theorem to solve problems.

LEARNS.EDU.VN provides resources and support for project-based learning, including project ideas, rubrics, and assessment tools.

9.4. Integration of Technology

Technology continues to play an increasingly important role in education, and new tools and resources are constantly being developed to enhance the teaching and learning of the Pythagorean theorem.

Virtual Reality: Use virtual reality to create immersive learning experiences that allow students to explore the Pythagorean theorem in a three-dimensional environment.
Augmented Reality: Incorporate augmented reality to overlay virtual information onto the real world, allowing students to see how the Pythagorean theorem is used in everyday life.
Artificial Intelligence: Utilize artificial intelligence to provide personalized feedback and support to students as they learn the Pythagorean theorem.

LEARNS.EDU.VN integrates the latest technologies into its learning resources, offering virtual reality experiences, augmented reality applications, and artificial intelligence-powered support to enhance the learning experience.

Table: Updated Information and Trends in Teaching Pythagorean Theorem

Category	Description	Benefits	Examples
Personalized Learning	Tailoring instruction to meet individual student needs and learning styles.	Enhanced engagement, improved understanding, increased retention.	Adaptive assessments, flexible pacing, choice-based activities.
Gamification	Incorporating game-like elements into the learning experience to make it more engaging and motivating.	Increased motivation, enhanced engagement, improved learning outcomes.	Online games, classroom competitions, badges and leaderboards.
Project-Based Learning	Engaging students in real-world projects that require them to apply their knowledge and skills to solve authentic problems.	Deeper understanding, improved problem-solving skills, enhanced creativity.	Design a building, plan a trip, create a game.
Integration of Tech	Utilizing the latest technologies to enhance the teaching and learning of the Pythagorean theorem.	Immersive learning experiences, personalized feedback, enhanced engagement.	Virtual reality, augmented reality, artificial intelligence.

10. Frequently Asked Questions (FAQs)

This section addresses some frequently asked questions about the Pythagorean theorem.

10.1. What is the Pythagorean Theorem?

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship is expressed by the equation: $a^2 + b^2 = c^2$.

10.2. When is the Pythagorean Theorem Typically Taught?

The Pythagorean theorem is typically introduced in middle school, around the 7th or 8th grade.

10.3. Why is the Pythagorean Theorem Important?

The Pythagorean theorem is important because it is a fundamental concept in geometry with numerous applications in various fields, including construction, navigation, engineering, and computer science.

10.4. Does the Pythagorean Theorem Only Apply to Right Triangles?

Yes, the Pythagorean theorem only applies to right triangles.

10.5. What are Pythagorean Triples?

Pythagorean triples are sets of three positive integers that satisfy the Pythagorean theorem (e.g., 3-4-5, 5-12-13).

10.6. How is the Pythagorean Theorem Used in Real Life?

The Pythagorean theorem is used in various real-life applications, such as calculating distances, designing buildings, navigating ships and airplanes, and creating computer graphics.

10.7. How Can I Help My Child Understand the Pythagorean Theorem?

You can help your child understand the Pythagorean theorem by providing a supportive learning environment, utilizing online resources, connecting math to real life, and encouraging practice and review.

10.8. What are Some Common Mistakes Students Make When Learning the Pythagorean Theorem?

Some common mistakes students make include difficulty identifying the hypotenuse, incorrectly applying the formula, confusion with non-right triangles, difficulty with square roots, and lack of real-world context.

10.9. What are Some Advanced Topics Related to the Pythagorean Theorem?

Advanced topics related to the Pythagorean theorem include Pythagorean triples, the distance formula, trigonometry, and three-dimensional geometry.

10.10. Where Can I Find More Resources on the Pythagorean Theorem?

You can find more resources on the Pythagorean theorem at LEARNS.EDU.VN, which offers comprehensive lessons, practice problems, interactive simulations, and real-world examples.

Mastering the Pythagorean theorem opens doors to a deeper understanding of mathematics and its applications. At LEARNS.EDU.VN, we are committed to providing you with the tools and resources you need to succeed. Explore our website today and unlock your full potential!

Ready to dive deeper into the world of mathematics? LEARNS.EDU.VN offers a wide range of courses and resources designed to help you master the Pythagorean theorem and other essential concepts. Visit our website at learns.edu.vn or contact us at 123 Education Way, Learnville, CA 90210, United States, or Whatsapp: +1 555-555-1212 to learn more.