1. Introduction: Understanding Trigonometric Functions
When Do You Learn Sin Cos Tan? This is a question many students ask as they embark on their mathematical journey. Trigonometric functions, including sine (sin), cosine (cos), and tangent (tan), are fundamental concepts in mathematics with wide-ranging applications in fields like physics, engineering, and computer graphics. They are not just abstract ideas but powerful tools that help us understand relationships between angles and sides of triangles. LEARNS.EDU.VN is here to guide you through the process of understanding these essential functions. Learn about the usefulness of these functions and trigonometric identities.
LEARNS.EDU.VN is dedicated to providing accessible and comprehensive educational resources to help learners of all ages master trigonometric functions. We offer a variety of learning materials, including detailed articles, step-by-step tutorials, and interactive exercises, designed to make complex concepts easy to understand. Whether you are a student preparing for an exam or a professional seeking to refresh your knowledge, LEARNS.EDU.VN has the resources you need to succeed.
2. The Initial Encounter: Geometry and Right Triangles
2.1. Introduction to Trigonometry in Geometry
The first formal introduction to sin, cos, and tan typically occurs in high school geometry courses, specifically when students begin to study right triangles. A right triangle is defined as a triangle containing one angle of 90 degrees.
2.2. Key Concepts: Angles and Sides of Right Triangles
In the context of right triangles, trigonometry is used to relate the angles and the lengths of their sides. The three primary trigonometric ratios—sine, cosine, and tangent—are each defined as a ratio of two sides of a right triangle relative to one of its acute angles (an angle less than 90 degrees).
- Sine (sin): The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The cosine of an angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
2.3. The Mnemonic: SOH CAH TOA
A useful mnemonic to remember these ratios is SOH CAH TOA:
- SOH: Sine = Opposite / Hypotenuse
- CAH: Cosine = Adjacent / Hypotenuse
- TOA: Tangent = Opposite / Adjacent
This mnemonic serves as a quick reference, helping students recall the definitions of the trigonometric functions when solving problems involving right triangles.
3. Expanding Horizons: Algebra II and Trigonometric Functions
3.1. Extending the Concepts in Algebra II
After geometry, students usually encounter trigonometric functions again in Algebra II. In this course, the focus shifts from right triangles to the broader concept of trigonometric functions defined on the unit circle.
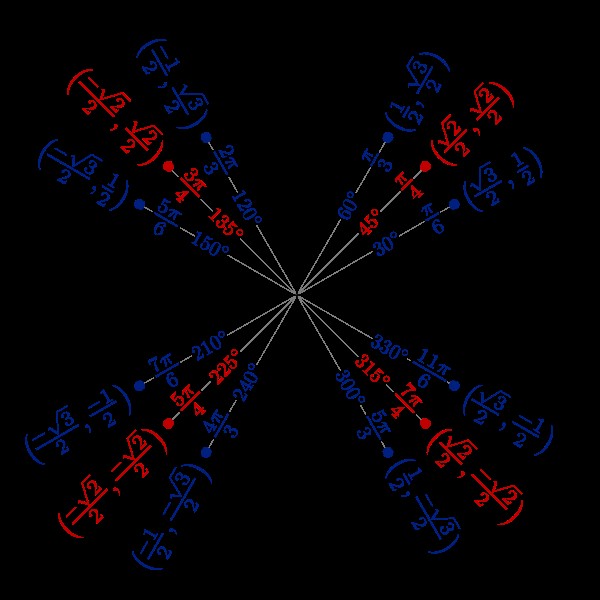
3.2. The Unit Circle: A Foundation for Trigonometry
The unit circle is a circle with a radius of one, centered at the origin of a coordinate plane. It provides a way to define trigonometric functions for any angle, not just those in a right triangle.
- Sine (sin): On the unit circle, the sine of an angle is the y-coordinate of the point where the terminal side of the angle intersects the circle.
- Cosine (cos): The cosine of an angle is the x-coordinate of the point where the terminal side of the angle intersects the circle.
- Tangent (tan): The tangent of an angle is the ratio of the y-coordinate to the x-coordinate (y/x). It can also be understood as sin(θ) / cos(θ).
3.3. Radian Measure: A New Way to Measure Angles
In Algebra II, students also learn about radian measure, which provides an alternative way to measure angles. One radian is defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle.
- Conversion: To convert degrees to radians, multiply by π/180. To convert radians to degrees, multiply by 180/π.
Radian measure is particularly useful in calculus and other advanced mathematics courses because it simplifies many formulas involving trigonometric functions.
3.4. Trigonometric Identities: Tools for Simplification
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variables for which the functions are defined. These identities are used to simplify trigonometric expressions and solve trigonometric equations.
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1
- Reciprocal Identities: csc(θ) = 1/sin(θ), sec(θ) = 1/cos(θ), cot(θ) = 1/tan(θ)
- Quotient Identities: tan(θ) = sin(θ)/cos(θ), cot(θ) = cos(θ)/sin(θ)
Understanding and applying these identities is crucial for advanced problem-solving in trigonometry.
 Unit Circle Trigonometry
Unit Circle Trigonometry
4. Advanced Applications: Precalculus and Calculus
4.1. Deeper Dive in Precalculus
Precalculus provides a more in-depth exploration of trigonometric functions, building on the concepts introduced in Algebra II. Students learn about the graphs of trigonometric functions, inverse trigonometric functions, and trigonometric equations.
4.2. Graphs of Trigonometric Functions
The graphs of sine, cosine, and tangent functions are periodic, meaning they repeat their values at regular intervals. Understanding these graphs is essential for analyzing and modeling real-world phenomena.
- Sine Function (y = sin(x)): The sine function has a period of 2π, an amplitude of 1, and oscillates between -1 and 1.
- Cosine Function (y = cos(x)): The cosine function also has a period of 2π and an amplitude of 1, but it is shifted π/2 units to the left compared to the sine function.
- Tangent Function (y = tan(x)): The tangent function has a period of π and vertical asymptotes at x = (n + 1/2)π, where n is an integer.
4.3. Inverse Trigonometric Functions
Inverse trigonometric functions, such as arcsin, arccos, and arctan, are used to find the angle that corresponds to a given trigonometric ratio. These functions are essential for solving equations where the angle is unknown.
- arcsin(x) or sin⁻¹(x): The inverse sine function returns the angle whose sine is x.
- arccos(x) or cos⁻¹(x): The inverse cosine function returns the angle whose cosine is x.
- arctan(x) or tan⁻¹(x): The inverse tangent function returns the angle whose tangent is x.
4.4. Trigonometric Equations: Solving for Unknown Angles
Trigonometric equations involve trigonometric functions and require solving for the unknown angle. These equations can be solved using algebraic techniques, trigonometric identities, and inverse trigonometric functions.
4.5. Trigonometry in Calculus
In calculus, trigonometric functions are used extensively in differentiation and integration. Understanding the derivatives and integrals of trigonometric functions is crucial for solving many calculus problems.
- Derivatives:
- d/dx (sin(x)) = cos(x)
- d/dx (cos(x)) = -sin(x)
- d/dx (tan(x)) = sec²(x)
- Integrals:
- ∫ sin(x) dx = -cos(x) + C
- ∫ cos(x) dx = sin(x) + C
- ∫ sec²(x) dx = tan(x) + C
These derivatives and integrals are used to solve a wide range of problems in calculus, including finding areas, volumes, and rates of change.
5. Real-World Applications of Sin Cos Tan
5.1. Physics: Analyzing Motion and Waves
Trigonometric functions are essential in physics for analyzing oscillatory motion, such as simple harmonic motion and wave phenomena. They are used to describe the position, velocity, and acceleration of objects moving in periodic patterns.
- Simple Harmonic Motion: The motion of a mass attached to a spring can be described using sine and cosine functions.
- Wave Phenomena: Trigonometric functions are used to model the amplitude, frequency, and phase of waves, such as sound waves and electromagnetic waves.
5.2. Engineering: Designing Structures and Systems
Engineers use trigonometric functions to design and analyze structures, circuits, and control systems. They are used to calculate forces, stresses, and strains in structural components.
- Structural Analysis: Trigonometry is used to determine the angles and forces in trusses, bridges, and other structures.
- Circuit Analysis: Trigonometric functions are used to analyze alternating current (AC) circuits, which involve sinusoidal voltages and currents.
5.3. Computer Graphics: Creating Visual Effects
In computer graphics, trigonometric functions are used to create realistic visual effects, such as rotations, scaling, and transformations of objects in 3D space. They are also used in animation and game development.
- Rotations: Trigonometric functions are used to rotate objects around an axis in 2D and 3D space.
- Transformations: Trigonometry is used to transform objects, such as scaling, shearing, and projecting them onto a 2D screen.
5.4. Navigation: Determining Position and Direction
Trigonometric functions are used in navigation to determine position, direction, and distance. They are used in GPS systems, compasses, and other navigational tools.
- GPS Systems: Trigonometry is used to calculate the position of a GPS receiver based on signals from multiple satellites.
- Compass Navigation: Trigonometry is used to calculate the bearing and distance to a destination based on compass readings and maps.
5.5. Music: Understanding Sound and Harmony
Trigonometry helps in understanding the mathematical relationships in music, such as the frequencies and amplitudes of sound waves, which are often modeled using sine and cosine functions.
- Sound Waves: The frequency and amplitude of sound waves can be described using trigonometric functions.
- Harmonic Analysis: Trigonometry is used to analyze the harmonic content of musical sounds, which contributes to their unique timbre and character.
| Application | Description |
|---|---|
| Physics | Analyzing oscillatory motion, wave phenomena |
| Engineering | Designing structures, circuits, and control systems |
| Computer Graphics | Creating visual effects, rotations, transformations |
| Navigation | Determining position, direction, and distance |
| Music | Understanding sound and harmony |
6. Making Trigonometry Accessible: Tips and Tricks
6.1. Visual Aids: Diagrams and Graphs
Visual aids, such as diagrams and graphs, can help students visualize trigonometric concepts and understand their relationships. Use diagrams to illustrate right triangles and the unit circle, and use graphs to show the behavior of trigonometric functions.
6.2. Real-World Examples: Connecting to Practical Applications
Connecting trigonometric concepts to real-world examples can make them more relatable and easier to understand. Discuss how trigonometry is used in fields like physics, engineering, and computer graphics to demonstrate its practical significance.
6.3. Practice Problems: Reinforcing Learning
Solving practice problems is essential for reinforcing learning and developing problem-solving skills. Provide students with a variety of problems that require them to apply trigonometric concepts in different contexts.
6.4. Online Resources: Leveraging Technology
Online resources, such as tutorials, videos, and interactive exercises, can supplement classroom instruction and provide students with additional support. Websites like LEARNS.EDU.VN offer a wealth of resources for learning trigonometry.
6.5. Mnemonics: Aiding Recall
Using mnemonics, such as SOH CAH TOA, can help students remember the definitions of trigonometric functions and other key concepts. Encourage students to create their own mnemonics to aid recall.
6.6. Study Groups: Collaborative Learning
Collaborative learning can enhance understanding and retention of trigonometric concepts. Encourage students to form study groups and work together to solve problems and review material.
7. Common Challenges and How to Overcome Them
7.1. Understanding Radian Measure
Many students struggle with radian measure because it is a new way of measuring angles that is different from degrees. To overcome this challenge, provide students with plenty of practice converting between degrees and radians, and explain the concept of radian measure in terms of the unit circle.
7.2. Memorizing Trigonometric Identities
Memorizing trigonometric identities can be challenging because there are so many of them. To make it easier, focus on understanding the relationships between the identities and using them in practice problems. Provide students with a reference sheet of common identities and encourage them to create flashcards.
7.3. Applying Trigonometry in Word Problems
Applying trigonometry in word problems can be difficult because it requires translating real-world scenarios into mathematical equations. To overcome this challenge, teach students how to identify the key information in a word problem and draw diagrams to visualize the situation. Provide them with plenty of practice solving word problems and encourage them to work together to find solutions.
7.4. Visualizing Trigonometric Functions
Visualizing trigonometric functions and their graphs can be challenging for some students. Use visual aids, such as graphs and animations, to help them understand the behavior of trigonometric functions. Encourage them to use graphing calculators or online tools to explore the graphs of trigonometric functions and see how they change as parameters are varied.
8. Advanced Trigonometric Concepts
8.1. Trigonometric Series
Trigonometric series, such as Fourier series, are infinite sums of trigonometric functions that can be used to represent periodic functions. These series are used in signal processing, image compression, and other applications.
8.2. Spherical Trigonometry
Spherical trigonometry deals with the relationships between the sides and angles of spherical triangles, which are triangles drawn on the surface of a sphere. This branch of trigonometry is used in navigation, astronomy, and geodesy.
8.3. Hyperbolic Functions
Hyperbolic functions are analogous to trigonometric functions but are defined using hyperbolas instead of circles. These functions are used in physics, engineering, and mathematics.
- sinh(x) = (e^x – e^-x) / 2
- cosh(x) = (e^x + e^-x) / 2
- tanh(x) = sinh(x) / cosh(x)
8.4. Complex Numbers and Trigonometry
Complex numbers can be expressed in polar form using trigonometric functions, which simplifies many calculations involving complex numbers. Euler’s formula, e^(ix) = cos(x) + i sin(x), connects complex numbers, trigonometric functions, and exponential functions.
9. Tools and Resources for Learning Trigonometry
9.1. Textbooks and Workbooks
Textbooks and workbooks provide comprehensive coverage of trigonometric concepts and practice problems. Look for textbooks that include clear explanations, examples, and exercises.
9.2. Online Tutorials and Videos
Online tutorials and videos can supplement classroom instruction and provide students with additional support. Websites like Khan Academy and YouTube offer a wealth of resources for learning trigonometry.
9.3. Interactive Exercises and Games
Interactive exercises and games can make learning trigonometry more engaging and fun. Websites like Mathway and Wolfram Alpha offer interactive tools for solving trigonometric problems.
9.4. Graphing Calculators
Graphing calculators can be used to visualize trigonometric functions and solve trigonometric equations. They are particularly useful for exploring the graphs of trigonometric functions and seeing how they change as parameters are varied.
9.5. Software and Apps
Software and apps, such as GeoGebra and Desmos, can be used to create interactive diagrams and graphs that illustrate trigonometric concepts. These tools are particularly useful for visualizing trigonometric functions and exploring their properties.
9.6. LEARNS.EDU.VN Resources
LEARNS.EDU.VN provides a variety of resources for learning trigonometry, including detailed articles, step-by-step tutorials, and interactive exercises. Our resources are designed to make complex concepts easy to understand and help learners of all ages master trigonometry.
10. Integrating Technology in Trigonometry Education: A Modern Approach
10.1. Interactive Simulations and Modeling
Interactive simulations and modeling tools allow students to explore trigonometric concepts in a dynamic and engaging way. For instance, students can use simulations to visualize how changing the parameters of a trigonometric function affects its graph, or how trigonometric principles apply to real-world scenarios like wave propagation or pendulum motion.
10.2. Virtual Reality (VR) and Augmented Reality (AR)
VR and AR technologies offer immersive learning experiences that can enhance students’ understanding of trigonometry. VR can create virtual environments where students can interact with 3D models of geometric shapes and visualize trigonometric relationships in a spatial context. AR can overlay trigonometric concepts onto real-world objects, allowing students to see how these concepts apply in their everyday surroundings.
10.3. Adaptive Learning Platforms
Adaptive learning platforms use algorithms to personalize the learning experience for each student. These platforms assess students’ knowledge and skills, identify areas where they need additional support, and provide targeted instruction and practice. This personalized approach can help students master trigonometric concepts more efficiently and effectively.
10.4. Mobile Learning Apps
Mobile learning apps provide students with access to trigonometric resources and activities anytime, anywhere. These apps often include features like video tutorials, practice quizzes, and interactive simulations, allowing students to learn at their own pace and on their own schedule.
10.5. Collaborative Online Tools
Collaborative online tools, such as shared whiteboards and document editors, enable students to work together on trigonometric problems and projects in real-time. These tools promote collaboration, communication, and critical thinking skills, as students share ideas, discuss strategies, and solve problems together.
10.6. Data Analytics and Assessment
Data analytics tools can be used to track students’ progress in trigonometry and identify areas where they are struggling. Teachers can use this data to inform their instruction, provide targeted support to students, and adjust their teaching strategies as needed. Assessment tools, such as online quizzes and tests, can provide students with feedback on their understanding of trigonometric concepts and help them identify areas where they need to improve.
| Technology | Description | Benefits |
|---|---|---|
| Interactive Simulations | Dynamic tools that allow students to explore trigonometric concepts by manipulating variables and observing their effects. | Enhances understanding of cause-and-effect relationships; improves engagement and retention. |
| VR and AR | Immersive technologies that create virtual or augmented environments where students can interact with 3D models and spatial representations of trigonometric concepts. | Provides a more intuitive and memorable learning experience; fosters spatial reasoning skills. |
| Adaptive Learning Platforms | Personalized learning systems that adjust the difficulty and content based on each student’s performance and needs. | Ensures that students receive targeted instruction and practice; maximizes learning efficiency; promotes self-paced learning. |
| Mobile Learning Apps | Portable applications that provide access to trigonometric resources, tutorials, quizzes, and simulations on smartphones and tablets. | Offers flexibility and convenience; allows students to learn anytime, anywhere; provides access to a wide range of resources. |
| Collaborative Online Tools | Platforms that enable students to work together on trigonometric problems and projects in real-time, sharing ideas and strategies. | Promotes collaboration, communication, and critical thinking skills; fosters a sense of community. |
| Data Analytics and Assessment | Tools that track students’ progress, identify areas of struggle, and provide feedback on their understanding of trigonometric concepts. | Informs instruction and allows teachers to provide targeted support; helps students identify areas where they need to improve; promotes data-driven decision-making. |
11. Strategies for Effective Trigonometry Teaching
11.1. Emphasize Conceptual Understanding
Instead of focusing solely on memorization and rote application of formulas, teachers should emphasize conceptual understanding of trigonometric principles. This involves explaining the underlying logic behind trigonometric relationships, connecting them to real-world examples, and encouraging students to ask questions and explore different perspectives.
11.2. Use a Variety of Teaching Methods
To cater to different learning styles and preferences, teachers should use a variety of teaching methods, including lectures, discussions, demonstrations, group activities, and hands-on projects. This variety can help keep students engaged and motivated, and ensure that they have multiple opportunities to grasp trigonometric concepts.
11.3. Provide Ample Practice Opportunities
Practice is essential for mastering trigonometry. Teachers should provide students with ample opportunities to solve problems, both in class and at home. This practice should include a mix of routine exercises and challenging problems that require students to apply their knowledge in novel ways.
11.4. Offer Individualized Support
Some students may struggle with trigonometry more than others. Teachers should offer individualized support to these students, providing them with additional instruction, practice, and feedback. This support can take the form of one-on-one tutoring, small-group sessions, or online resources.
11.5. Make Connections to Other Subjects
Trigonometry is not an isolated subject. It is connected to many other areas of mathematics, science, and engineering. Teachers should make these connections explicit, showing students how trigonometry is used in other fields. This can help students appreciate the relevance and importance of trigonometry, and motivate them to learn it.
11.6. Foster a Positive Learning Environment
A positive learning environment is essential for effective trigonometry teaching. Teachers should create a classroom where students feel safe, respected, and supported. They should encourage students to take risks, ask questions, and learn from their mistakes.
12. Trigonometry Competitions and Challenges: Enhancing Skills
12.1. Math Competitions
Participating in math competitions like the American Mathematics Competition (AMC), the Math Olympiad, and local math leagues can be an excellent way for students to enhance their trigonometry skills. These competitions often include challenging problems that require a deep understanding of trigonometric concepts and problem-solving strategies.
12.2. Online Math Challenges
Numerous websites and platforms offer online math challenges and quizzes that focus on trigonometry. These challenges can provide students with a fun and engaging way to test their knowledge and improve their skills.
12.3. Trigonometry-Based Projects
Engaging in trigonometry-based projects can provide students with hands-on experience applying trigonometric concepts to real-world problems. These projects can range from designing structures to analyzing motion or creating computer graphics.
12.4. Math Clubs and Teams
Joining a math club or team can provide students with opportunities to collaborate with peers, learn from experienced mentors, and participate in competitions and challenges. These clubs and teams often focus on developing problem-solving skills and promoting a love of mathematics.
12.5. Summer Math Programs
Attending summer math programs can provide students with intensive instruction and practice in trigonometry. These programs often cover advanced topics and offer opportunities for students to work on challenging projects.
12.6. Creating Math Games
Designing and developing math games that incorporate trigonometric concepts can be a fun and creative way for students to learn and reinforce their understanding. This activity can also promote critical thinking, problem-solving, and computer programming skills.
13. The Role of Trigonometry in Standardized Tests
13.1. SAT and ACT
Trigonometry concepts are typically tested on standardized tests such as the SAT and ACT. Understanding trigonometric functions, identities, and applications is crucial for achieving a high score on these exams.
13.2. College Placement Exams
Many colleges use placement exams to determine students’ readiness for college-level math courses. Trigonometry is often a key component of these exams, assessing students’ ability to apply trigonometric concepts to solve problems.
13.3. AP Calculus and Physics Exams
Students taking Advanced Placement (AP) Calculus and Physics exams need a strong foundation in trigonometry. These exams often include problems that require students to use trigonometric functions, identities, and derivatives/integrals to solve calculus and physics problems.
13.4. GRE and GMAT
Graduate Record Examinations (GRE) and Graduate Management Admission Test (GMAT) may include questions that require knowledge of basic trigonometry. While trigonometry is not a primary focus of these exams, understanding trigonometric concepts can be helpful for solving certain types of quantitative problems.
13.5. Professional Licensing Exams
Some professional licensing exams, such as those for engineering and architecture, may include questions that require knowledge of trigonometry. These exams assess candidates’ ability to apply trigonometric concepts to solve practical problems in their respective fields.
13.6. Preparing for Standardized Tests
To prepare for standardized tests that include trigonometry, students should review trigonometric concepts, practice solving problems, and take practice tests. Resources such as textbooks, online tutorials, and test preparation materials can be helpful for this preparation.
14. The Future of Trigonometry Education
14.1. Personalized Learning
Personalized learning approaches, which tailor instruction to meet the individual needs and learning styles of each student, are likely to become more prevalent in trigonometry education. These approaches can help students master trigonometric concepts more efficiently and effectively.
14.2. Technology Integration
Technology will continue to play an increasingly important role in trigonometry education. Interactive simulations, virtual reality, and adaptive learning platforms can enhance students’ understanding and engagement with trigonometric concepts.
14.3. Real-World Applications
Emphasis on real-world applications of trigonometry is likely to increase. Connecting trigonometric concepts to practical problems in fields such as physics, engineering, and computer graphics can help students appreciate the relevance and importance of trigonometry.
14.4. Interdisciplinary Connections
Interdisciplinary connections between trigonometry and other subjects, such as science, engineering, and art, are likely to be emphasized. This can help students see the connections between different areas of knowledge and develop a more holistic understanding of the world.
14.5. Inquiry-Based Learning
Inquiry-based learning approaches, which encourage students to explore trigonometric concepts through hands-on activities and investigations, are likely to become more common. These approaches can help students develop critical thinking, problem-solving, and communication skills.
14.6. Assessment Innovation
Assessment methods in trigonometry education are likely to evolve to include more performance-based assessments, such as projects, presentations, and portfolios. These assessments can provide a more authentic and comprehensive evaluation of students’ understanding and skills.
15. Conclusion: Embrace the Power of Trigonometry
When do you learn sin cos tan? The journey begins in geometry and continues through algebra, precalculus, and beyond. Trigonometry is a powerful tool with countless applications in science, engineering, and technology. Understanding sin, cos, and tan is not just about memorizing formulas but about developing a deeper understanding of the relationships between angles and sides, which opens doors to solving complex problems and exploring the world around us. LEARNS.EDU.VN encourages you to embrace the power of trigonometry and continue your learning journey with us.
LEARNS.EDU.VN offers a wealth of resources to support your learning, from detailed articles and tutorials to interactive exercises and quizzes. Whether you are a student, teacher, or lifelong learner, we are here to help you master trigonometry and unlock its potential. Visit LEARNS.EDU.VN today and discover the fascinating world of trigonometric functions and their applications.
Ready to dive deeper into trigonometry and unlock its potential? Visit LEARNS.EDU.VN today to explore our comprehensive resources and courses. Whether you’re looking to master the basics or tackle advanced concepts, we’re here to support your learning journey. Don’t wait – start exploring now!
Contact us:
- Address: 123 Education Way, Learnville, CA 90210, United States
- WhatsApp: +1 555-555-1212
- Website: LEARNS.EDU.VN
16. FAQ: Frequently Asked Questions About Trigonometry
16.1. What are the primary trigonometric functions?
The primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions relate the angles of a right triangle to the ratios of its sides.
16.2. What is SOH CAH TOA?
SOH CAH TOA is a mnemonic used to remember the definitions of the trigonometric functions: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
16.3. What is the unit circle, and how is it used in trigonometry?
The unit circle is a circle with a radius of one, centered at the origin of a coordinate plane. It is used to define trigonometric functions for any angle, not just those in a right triangle.
16.4. What are trigonometric identities, and why are they important?
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variables for which the functions are defined. They are used to simplify trigonometric expressions and solve trigonometric equations.
16.5. How are trigonometric functions used in real-world applications?
Trigonometric functions are used in a variety of real-world applications, including physics, engineering, computer graphics, navigation, and music.
16.6. What are inverse trigonometric functions?
Inverse trigonometric functions, such as arcsin, arccos, and arctan, are used to find the angle that corresponds to a given trigonometric ratio.
16.7. How do I solve trigonometric equations?
Trigonometric equations can be solved using algebraic techniques, trigonometric identities, and inverse trigonometric functions.
16.8. What are the derivatives and integrals of trigonometric functions?
The derivatives and integrals of trigonometric functions are used extensively in calculus to solve problems involving rates of change, areas, and volumes.
16.9. How can I improve my understanding of trigonometry?
To improve your understanding of trigonometry, use visual aids, real-world examples, practice problems, online resources, mnemonics, and study groups.
16.10. Where can I find additional resources for learning trigonometry?
You can find additional resources for learning trigonometry at learns.edu.vn, as well as in textbooks, online tutorials, interactive exercises, and graphing calculators.